Задача 1.1. Расчет прямого ступенчатого стержня

Исходные данные:
| F1
, кН |
F4
, кН |
F6
, кН |
L1
, см |
L2
, см |
L3
, см |
A1
, см2
|
A2
, см2
|
A2
, см2
|
| 160 |
60 |
100 |
64 |
36 |
44 |
8 |
6 |
4 |
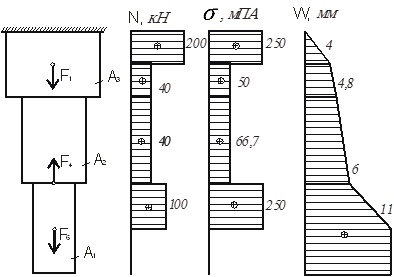
1) Построить эпюры продольных сил, напряжений и перемещений;
2) Оценить прочность стержня
1) С целью определений значений продольных сил в различных сечениях выделим характерные сечения трехступенчатого стержня, в которых найдем продольные силы. И построим эпюру продольных сил.
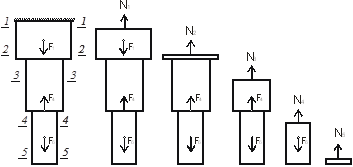
1.
Сечение 1–1
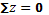
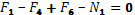
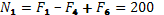 кН кН
2.
Сечение 2–2
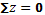
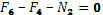
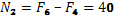 кН кН
3.
Сечение 3–3
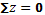
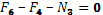
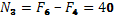 кН кН
4.
Сечение 4–4
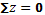
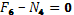
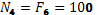 кН кН
5.
Сечение 5–5
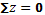
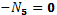
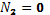 кН кН
2) На основании найденных значений продольных сил в характерных сечениях стержня строим эпюру продольных сил. Нормальные напряжения в тех же сечениях определим по формуле:
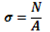 . .
И построим эпюру напряжений.
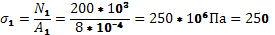 мПа мПа
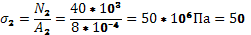 мПа мПа
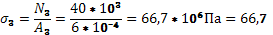 мПа мПа
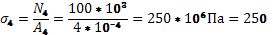 мПа мПа
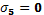
3) Вычислим деформации отдельных участков стержня по формуле:
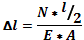
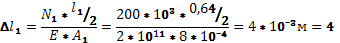 мм мм
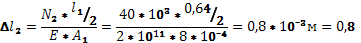 мм мм
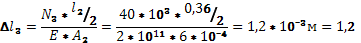 мм мм
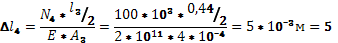 мм мм
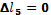
4) Найдем характерные перемещения стержня и построим их эпюры
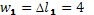 мм мм
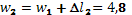 мм мм
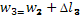 =6 мм =6 мм
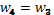 + +
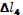 =11 мм =11 мм
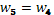 + +
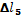 =11 мм =11 мм
5) Прочность материала стержня проверим в сечении, где наибольшее напряжение
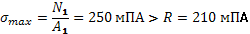
Следовательно, перенапряжение материала составляет:
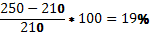
Задача 1.2. Геометрические характеристики плоских фигур
Для составного сечения необходимо определить:
1) Положение центра тяжести
2) Осевые и центробежные моменты инерции относительно центральных осей
3) Положение главных центральных осей
4) Вычислить значения главных центральных моментов инерции
5) Построить круг инерции и по нему проверить положение главных центральных осей и значения главных центральных моментов инерции
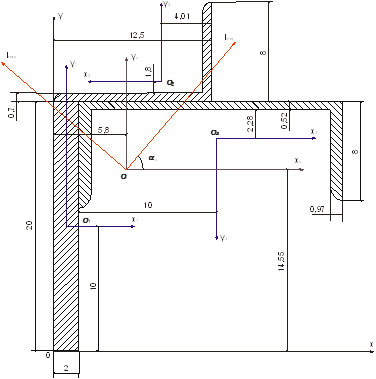
6) Вычертить сечение в удобном масштабе и показать все необходимые оси и размеры
Исходные данные:
| A, см2
|
Ix
, см4
|
Iy
, см4
|
Dxy
, см4
|
Лист 20 2 2 |
40 |
1333,3 |
13,3 |
- |
| Уголок 12,5/8 |
14,1 |
73,7 |
22,7 |
74,58 |
| Швейлер 20а |
25,2 |
139 |
1670 |
- |
Решение
1.
Найдем положение центра тяжести:
Sx
=A1
*y1
+ A2
*y2
+ A3
*y3
=10*40+21,8*14,1+17,72*25,2=1153,924 см3
Sy
= A1
*x1
+ A2
*x2
+ A3
*x3
=1*40+8,49*14,1+12*25,2=462,109 см3
Xc
=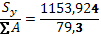 =5,8 см =5,8 см
Yc
=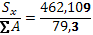 =14,55 см =14,55 см
2.
Вычислим значения осевых и центробежных моментов инерции относительно центральных осей:
IXc
=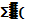 IXi
+Ai
*ai
2
)=73,7+1333,3+139+4,55*40+3,172
*25,2+7,252
*14,1=3368,46 см4 IXi
+Ai
*ai
2
)=73,7+1333,3+139+4,55*40+3,172
*25,2+7,252
*14,1=3368,46 см4
IYc
=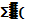 IYi
+Ai
*bi
2
)=13,3+227+1670+4,82
*40+2,692
*14,1+6,22
*25,2=3902,62 см4 IYi
+Ai
*bi
2
)=13,3+227+1670+4,82
*40+2,692
*14,1+6,22
*25,2=3902,62 см4
DXcYc
=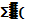 DXiYi
+Ai
*ai
*bi
)=0+(-4,55)*(-4,8)*40+74,58+7,25*2,69*14,1+3,17*6,2*25,2=1724,34 см4 DXiYi
+Ai
*ai
*bi
)=0+(-4,55)*(-4,8)*40+74,58+7,25*2,69*14,1+3,17*6,2*25,2=1724,34 см4
3.
Определим положение главных центральных осей инерции:
tg2α0
=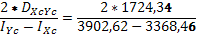 =6,456 =6,456 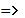 2α0
=81 2α0
=81 12,
=> α0
=40 12,
=> α0
=40 36, 36,
4.
Вычислим значения главных центральных моментов инерции:
Imax/main
=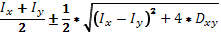
Imax
=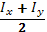 + + ==5380,44 см4 ==5380,44 см4
Imin
=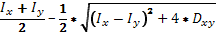 = =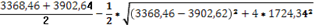 =1890,64 см4 =1890,64 см4
4.
Определим положение главных центральных осей через моменты инерции
Imax
и
Imin
:
tgα1
=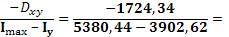 -1,167 -1,167
α1
=-49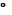 24, 24,
tgα2
=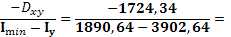 0,857 0,857
α2
=40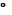 36, 36,
5.
Построим круг инерции и по нему проверим положение главных центральных осей и значения главных центральных моментов инерции:
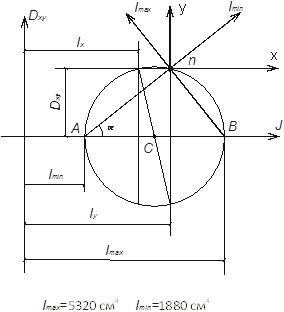
Задача 1.3. Изгиб балок
Проверка прочности балок при изгибе и исследование их деформации
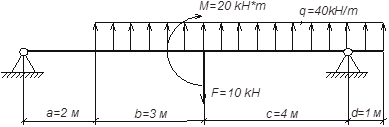
Исходные данные:
| a, м |
b, м |
c, м |
d, м |
F, kH |
q, kH/м |
M, kH*м |
| 2 |
3 |
4 |
1 |
10 |
40 |
20 |
Требуется:
1) построить эпюры поперечных сил и изгибающих моментов
2) подобрать сечение балки двутаврового профиля и проверить прочность принятого сечения по нормальным напряжениям с учетом собственного веса балки
3) вычислить наибольшее касательное напряжение в сечении с максимальным значением поперечной силы
4) в одном из сечений балки, где имеют Q и M большие значения, определить главные напряжения на уровне примыкания полки к стенке и проверить прочность материала по энергетической теории прочности
5) построить эпюры нормальных, касательных, главных и максимальных касательных напряжений в сечении, указанном в п. 4
6) определить аналитическим путем прогибы посередине пролета и на конце консоли и углы поворота сечений на опорах
7) с учетом вычисленных значений прогибов показать на схеме балки очертание ее изогнутой оси
8) проверить жесткость балки при допускаемом значении прогиба v=l/500 и модуле упругости E=2*105
Мпа
1) Определяем опорные реакции.
– Ra
*9+q*7*3,5+M-F*4-q*0,5=0
Ra
=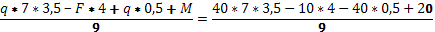 =104,4 kH =104,4 kH
– Rb
*9-F*5-M+q*8*6=0
Rb
=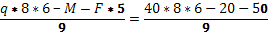 =205,6 kH =205,6 kH
Строим эпюры поперечных сил и изгибающих моментов.
1. Q1
=-Ra
=-104,4 kH
2. Q2
=-Ra
+q (z-2)=-104,4+120=-15,6 kH
3. Q3
=-Ra
+q (z-2) – F=104,4–10+40*7=165,6 kH
4. M1
=-Ra
*z=-104,4*2=-108,8 kH/m
5. M2
=-Ra
*z+ z=5 -104,4*5+20*32
=342 kH/m z=5 -104,4*5+20*32
=342 kH/m
z=6 -104,4*4+20*4=337,6 kH/m
z=7 -104,4*3+20=293,2 kH/m
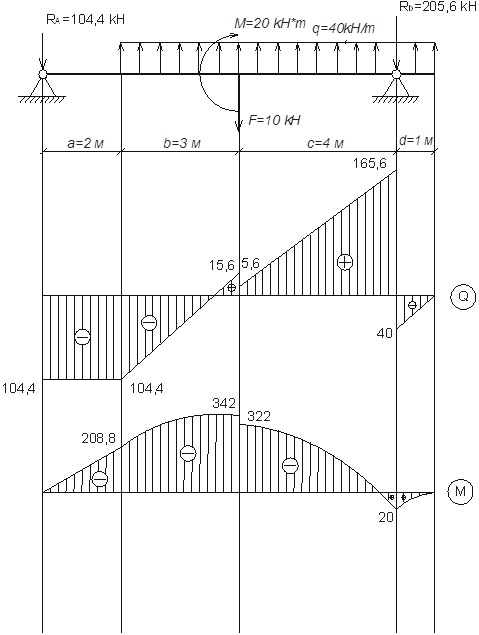
2) Построим сечение балки двутаврового профиля и проверим прочность принятого сечения по нормальным напряжениям с учетом собственного веса.
Wx
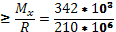 =1,6285*10-3
м3
=1628,5 см3 =1,6285*10-3
м3
=1628,5 см3
Подбираем двутавр:
№60
Ix
=75450 см4
Wx
= 2510 см3
Sx
=1450 см3
m=104 кг
Находим опорные реакции с учетом собственного веса.
– Ra
*9+q*7*3,5-F*4+M-q*0,5-q1
*9,45+q1
*0,5=0
Ra
=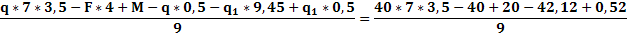 =99,8 kH =99,8 kH
– Rb
*9-F*5-M+q*8*6-q1
*10*5=0
Rb
=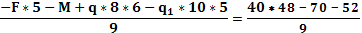 =199,8 kH =199,8 kH
Строим эпюры Q и M с учетом собственного веса.
Q1
=-Ra
-q1
*z=-99,8–1,04*2=-101,88 kH
Q2
=-Ra
-q1
*z+q*(z-2)=-99,8–5,2+40,3=15 kH
Q3
=-Ra
-q1
*z+q*(z-2) – F=-99,8–9,36+280–10=160,84 kH
M1
=-Ra
*z-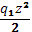 =-99,8*2–1,04*2=-201,68 kH/m =-99,8*2–1,04*2=-201,68 kH/m
M2
= Ra
*z-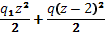 =-332 kH/m =-332 kH/m
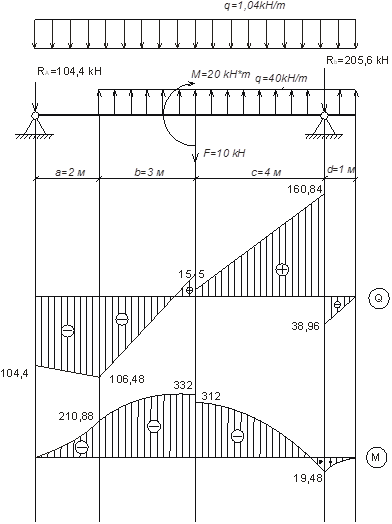
Проверим на прочность.
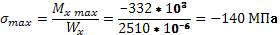
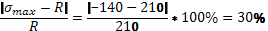
Недонапряжение составляет 30%
3) Вычислим наибольшее касательное напряжение в сечении с максимальным значением поперечной силы
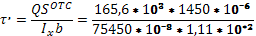 =28,67 МПа =28,67 МПа
4) В сечении балки, где
Q
и
M
имеют большее значение, определяем главное напряжение на уровне примыкания балки к стенке и проверяем прочность материала по энергетической теории прочности
M=208,8 kH/m
Q=104,4 kH
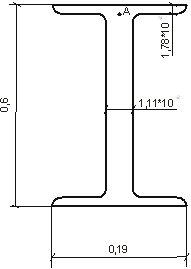
Определяем нормальные напряжения.
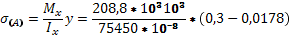 =78,1 МПа =78,1 МПа
Определяем касательные напряжения.
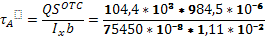 =12,3 МПа =12,3 МПа
Определяем главные напряжения.
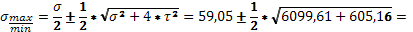 39,05±40,94 39,05±40,94
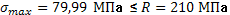
Проверяем прочность материала по энергетической теории.
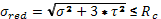
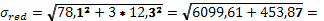 80,9 МПа 80,9 МПа
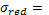 80,9 МПа ≤ 80,9 МПа ≤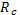 =140 МПа =140 МПа
5) Строим эпюры нормальных, касательных, главных и максимальных касательных напряжений.
Определяем нормальные напряжения
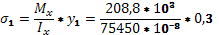 =83 МПа =83 МПа
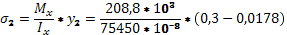 =78,1 МПа =78,1 МПа
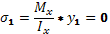
Определяем касательные напряжения.
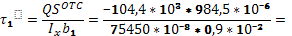 -0,78 МПа -0,78 МПа
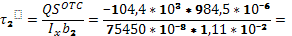 -12,3 МПа -12,3 МПа
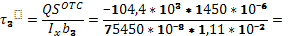 -18 МПа -18 МПа
Определяем главные напряжения.
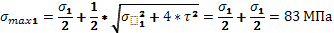
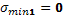
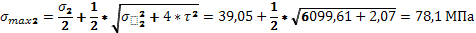
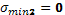
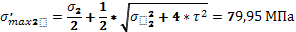
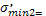 -1,89 МПа -1,89 МПа
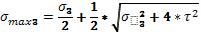 18 МПа 18 МПа
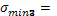 -18 МПа -18 МПа
Определяем максимальное касательное напряжение
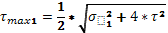 = =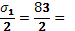 41,5 МПа 41,5 МПа
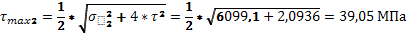
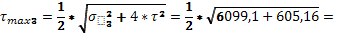 40,94 МПа 40,94 МПа
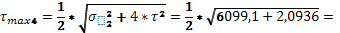 39,05 МПа 39,05 МПа
Строим эпюры.
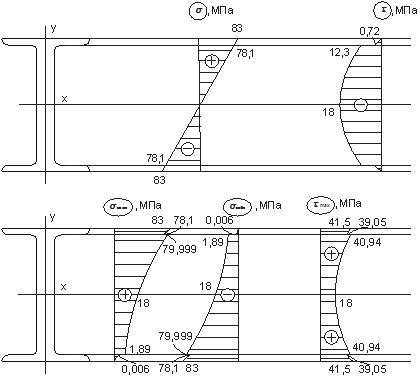
6) Определяем аналитическим путем прогибы посередине пролета и на конце консоли и углы поворота сечений на опорах.
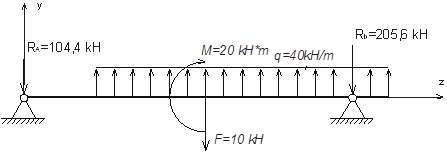
Уравнение углов поворота сечений.
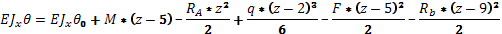
Уравнение прогибов.
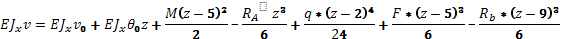
Находим начальные параметры:
При z=9, 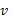 =0 =0
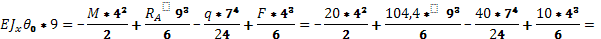 959 kH 959 kH
Значение прогиба по середине пролета:
При z=4,5
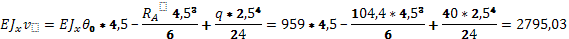
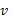 ср
= ср
= 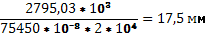
Значение прогиба на конце консоли.
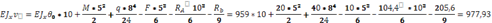
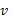 =- =- 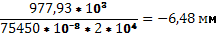
Угол поворота на опоре A.
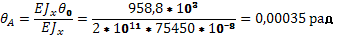
Угол поворота на опоре B.
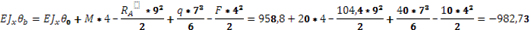
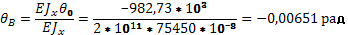
7)
C
учетом вычисленных значений прогибов, покажем на схеме балки очертания её изогнутой оси.

8) Проверим жесткость балки при допускаемом значении прогиба
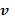 = =
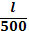 и модуля упругости
E
=2*105
МПа и модуля упругости
E
=2*105
МПа
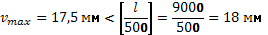
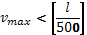
Условие по жесткости выполнено.
|