Белорусский государственный университет информатики и радиоэлектроники
Факультет компьютерных сетей и систем
Кафедра Информатики
Курсовой проект По курсу: Линейная алгебра и аналитическая геометрия
Тема: “ Исследование систем линейных уравнений неполного ранга и минимальным по Евклидовой норме решением”
Выполнил: Студент гр. 952 001 Лабкович О. А.
Проверил Борзенков А. В.
Минск 2000 Пусть задана система m линейных алгебраических уравнений с n неизвестными общего вида (СЛАУ) в матричной форме:
A*X = B где
A – основная матрица системы (или матрица коэффициентов при неизвестных) X – вектор-столбец решений системы (вектор неизвестных) B – вектор свободных коэффициентов
Решением системы такого вида называется всякий n – компонентный вектор-столбец X, обращающий матричное уравнение в тождество (равенство). Найдём решение с помощью метода последовательных исключений Жордана-Гаусса, который заключается в последовательном исключении неизвестных. Дополнительно выделим из множества решений вектор-решения минимальный по Евклидовой норме.
В MatLab стандартная функция rref(A), …/matlab/toolbox/matlab/matfun/rref.m, приводит матрицу A к треугольному виду на основе классического метода исключения Гаусса с частичным выбором ведущего элемента. В данной функции реализуется следующий код: который, не меняя местами столбцы матрицы системы, приводит матрицу к диагональному виду, работая только со строками(таким образом, использование этой функции не приведетк ошибкам).
% Loop over the entire matrix. % Перебор каждого элемента матрицы i = 1; j = 1; jb = []; while (i <= m) & (j <= n) % Find value and index of largest element in the remainder of column j. % Найти значение и индекс самого большого элемента в остатке от колонки j. [p,k] = max(abs(A(i:m,j))); k = k+i-1; if (p <= tol) % The column is negligible, zero it out. % Если остаток колонки незначителен, то обнуление остатка и переход на следующую иттерацию. A(i:m,j) = zeros(m-i+1,1); j = j + 1; else % Remember column index % Запоминание индекса колонки jb = [jb j]; % Swap i-th and k-th rows. % Поменияем месками i-ую и j-ую строки. A([i k],j:n) = A([k i],j:n); % Divide the pivot row by the pivot element. % Деление элементов текущей строки на текущий элемент A(i,j:n) = A(i,j:n)/A(i,j); % Subtract multiples of the pivot row from all the other rows. % Вычесть элементы текущей строки из всех других строк, начиная с j-го элемента. for k = [1:i-1 i+1:m] A(k,j:n) = A(k,j:n) - A(k,j)*A(i,j:n); end i = i + 1; j = j + 1; end end
Для этого, с помощью элементарных преобразований над строками и перестановки столбцов расширенную матрицу системы A|B (матрица, образованная добавлением столбца свободных коэффициентов B к основной матрице системы A) приведём к виду:
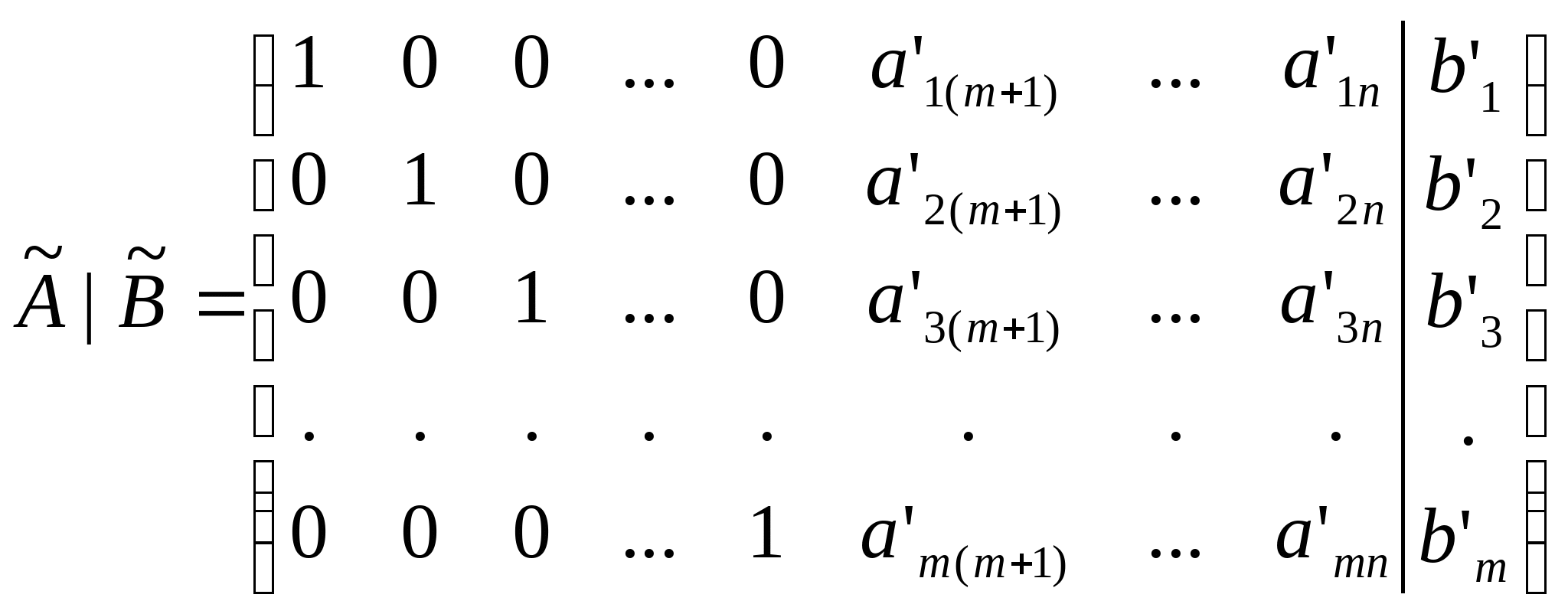
Необходимо отметить, что коэффициенты 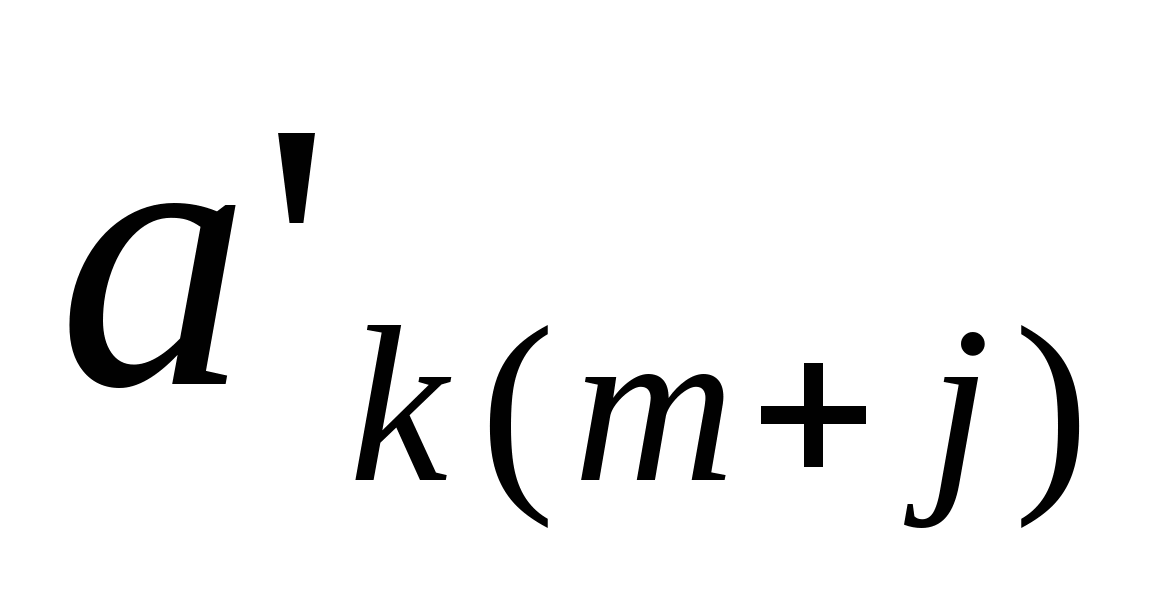 и и 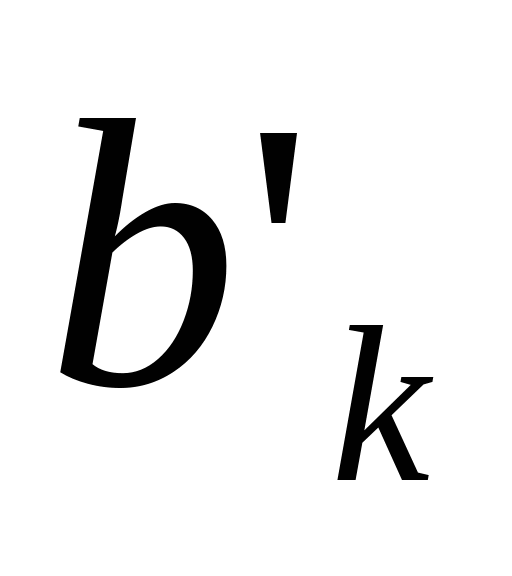 полученной матрицы, отличаются от исходных коэффициентов расширенной матрицы. То есть получены новые – основная матрица системы полученной матрицы, отличаются от исходных коэффициентов расширенной матрицы. То есть получены новые – основная матрица системы 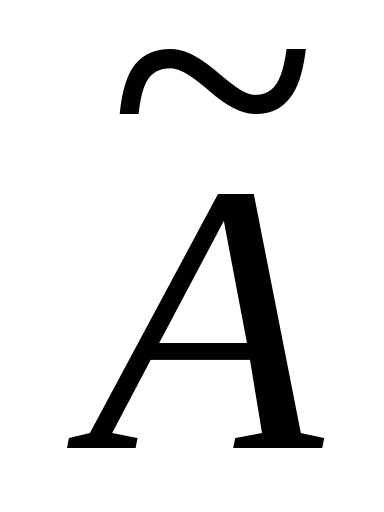 и вектор-столбец свободных коэффициентов и вектор-столбец свободных коэффициентов 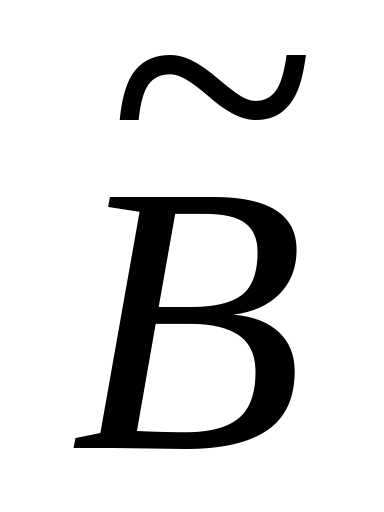 . Перемножив каждую строку матрицы . Перемножив каждую строку матрицы 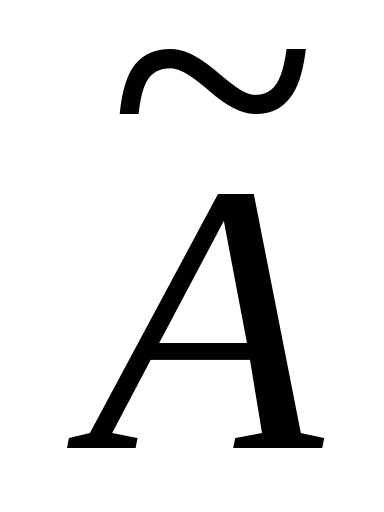 на вектор X получим: на вектор X получим:
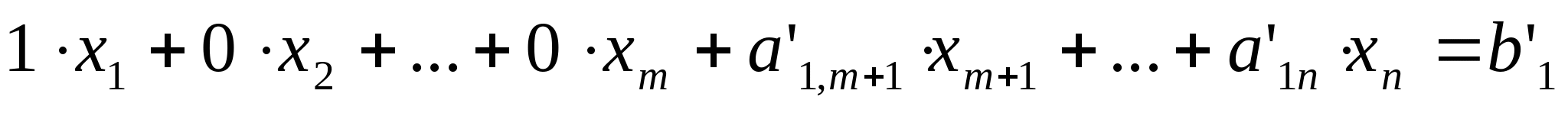
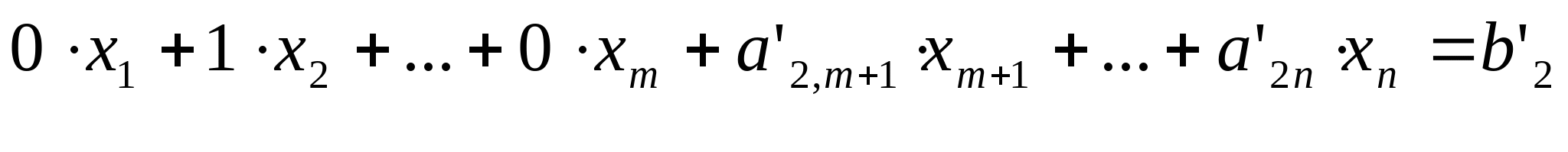

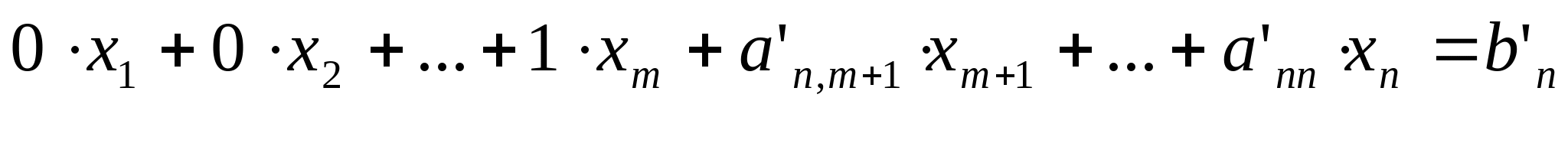
Тогда вектор-решения состоит из следующих компонент
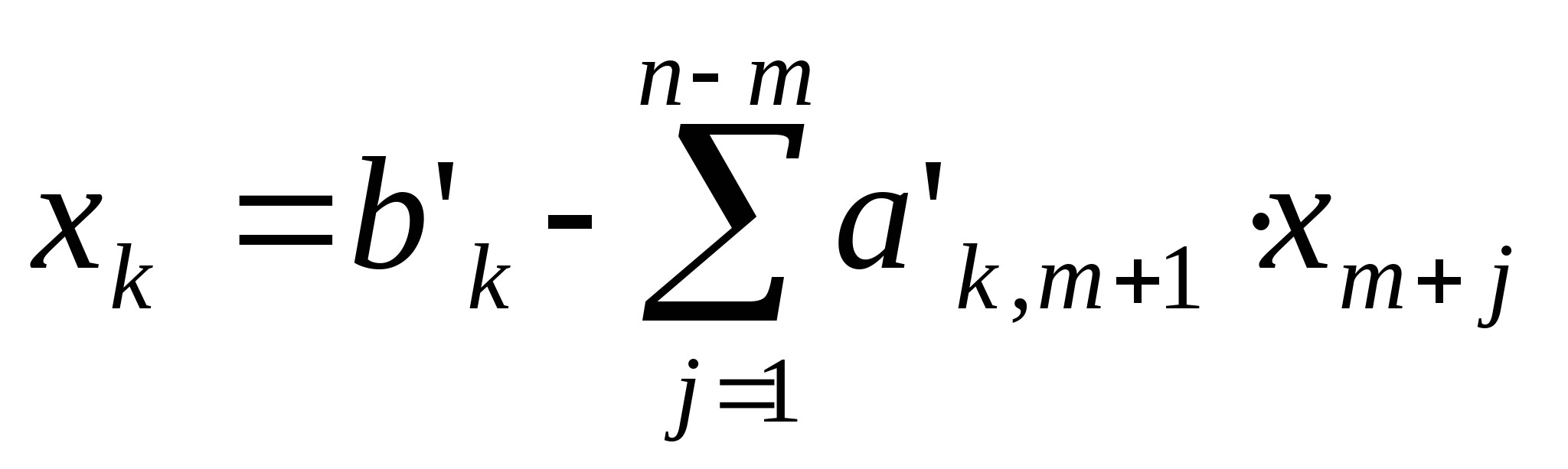 , где k = 1..m , где k = 1..m
Заменим 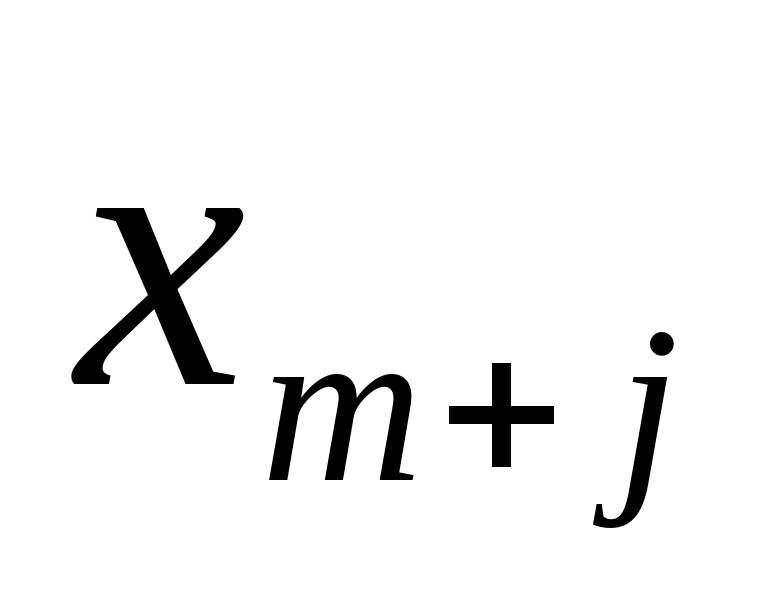 на коэффициенты на коэффициенты  , j = 1 .. n-m. Общее решение СЛАУ имеет вид , j = 1 .. n-m. Общее решение СЛАУ имеет вид 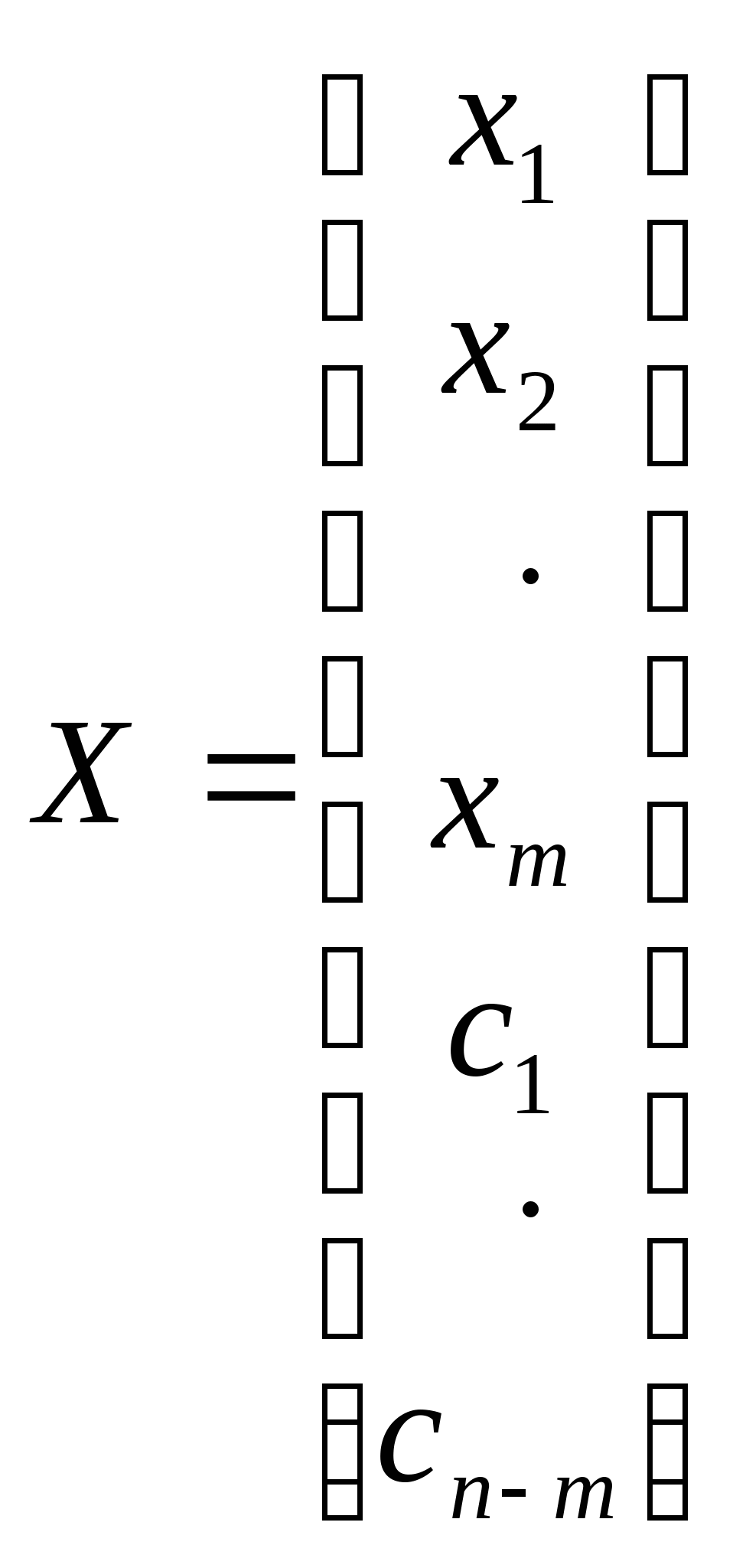
Подставляя различные числовые значения вместо 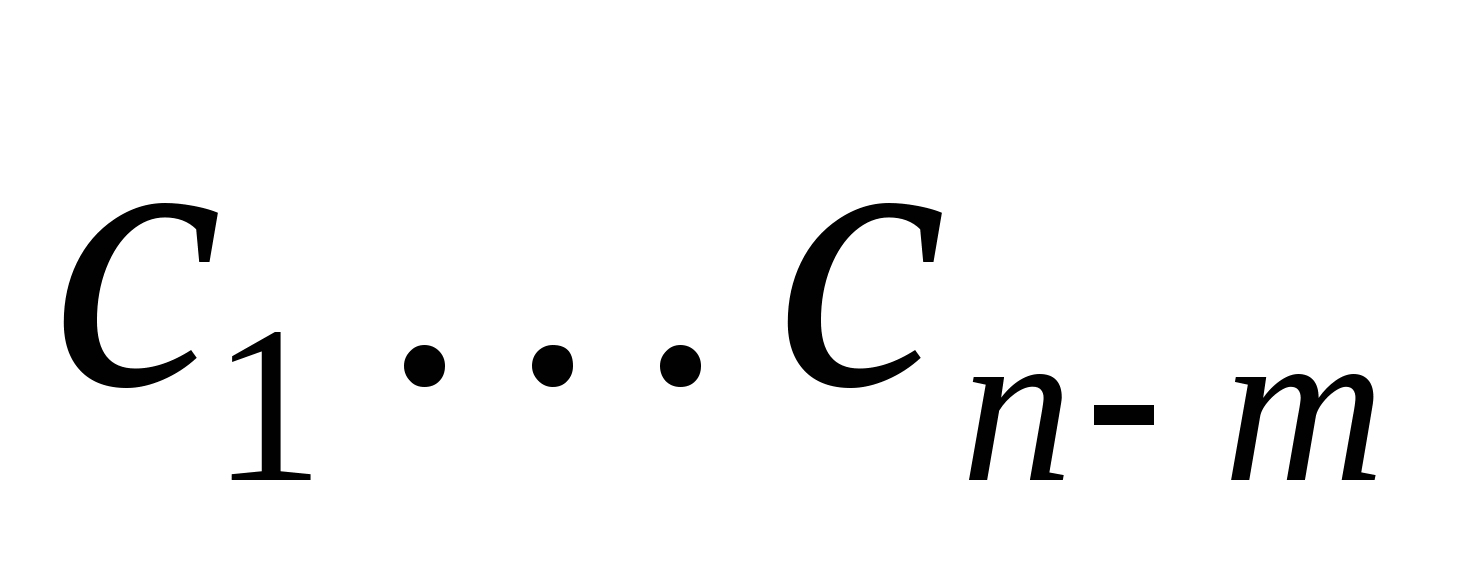 можно получить бесконечное множество частных решений. можно получить бесконечное множество частных решений.
Теперь из множества полученных решений необходимо выделить минимальное по Евклидовой норме, то есть найти соответствующие значения 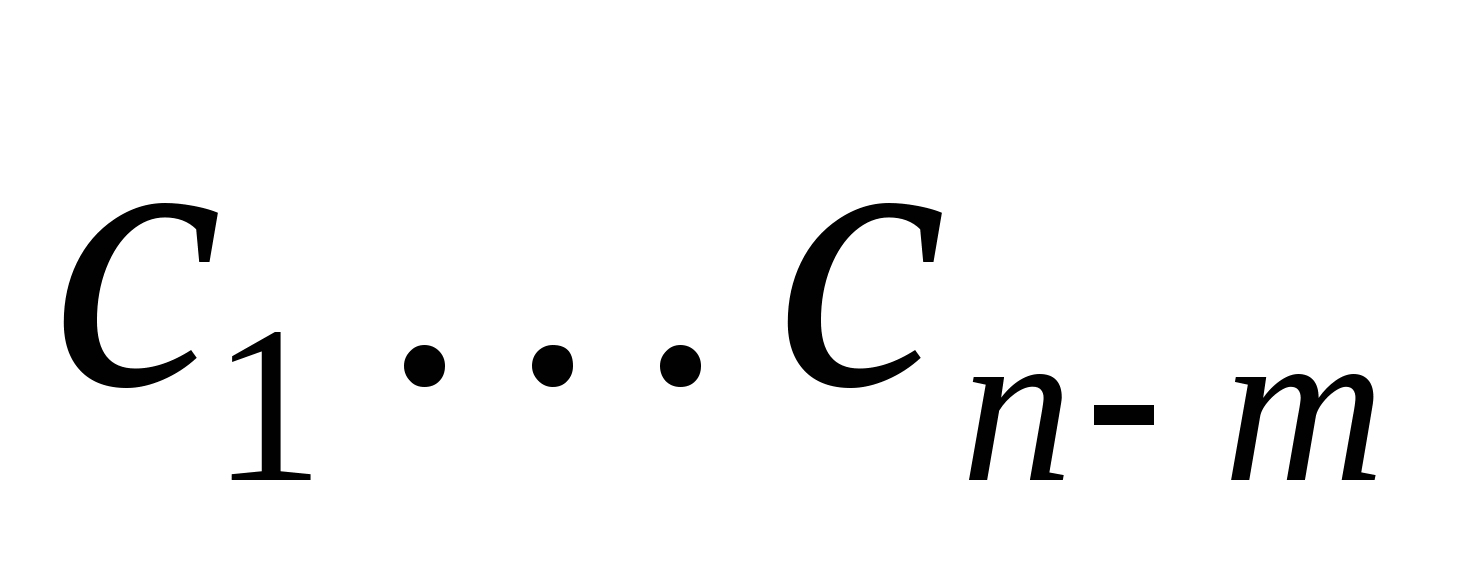 . . Евклидова норма: 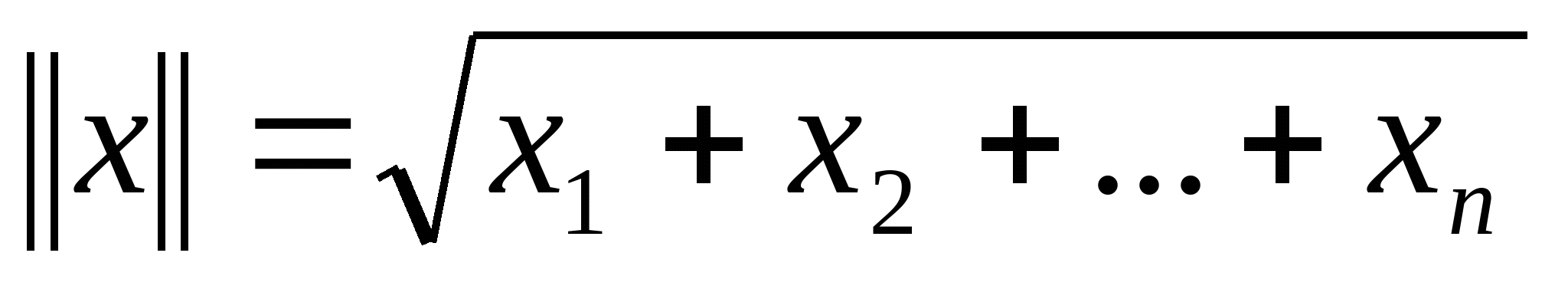 . Составим функцию . Составим функцию  . Нахождение решения минимального по норме эквивалентно нахождению значений компонентов вектора-решений . Нахождение решения минимального по норме эквивалентно нахождению значений компонентов вектора-решений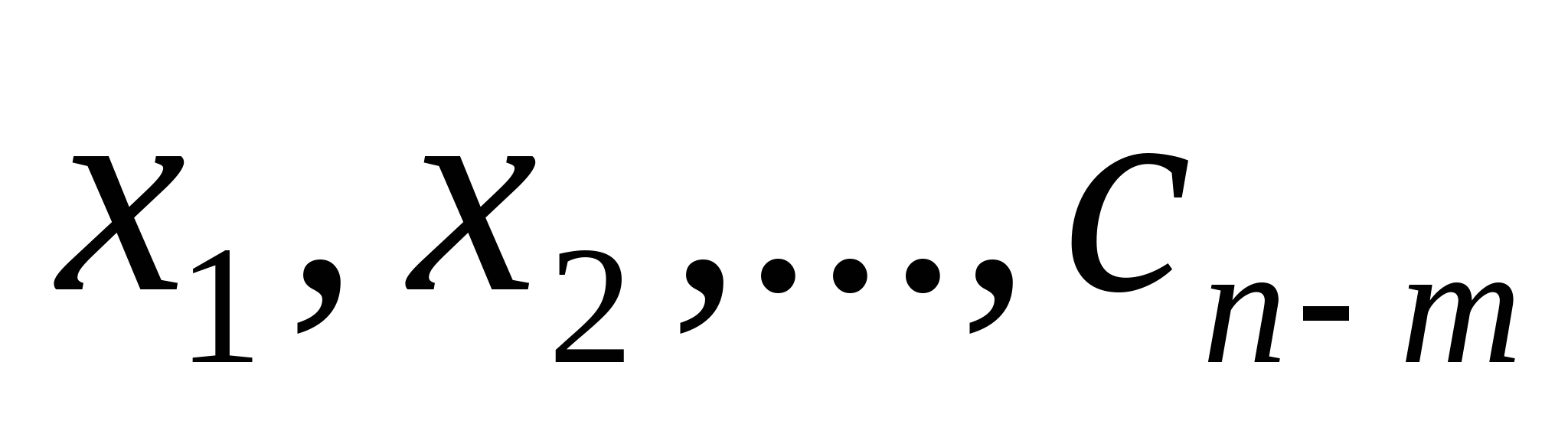 в точке минимума функции F. По необходимому признаку экстремума функции нескольких переменных и в силу выпуклости функции вниз минимум функции соответствует условиям: в точке минимума функции F. По необходимому признаку экстремума функции нескольких переменных и в силу выпуклости функции вниз минимум функции соответствует условиям:
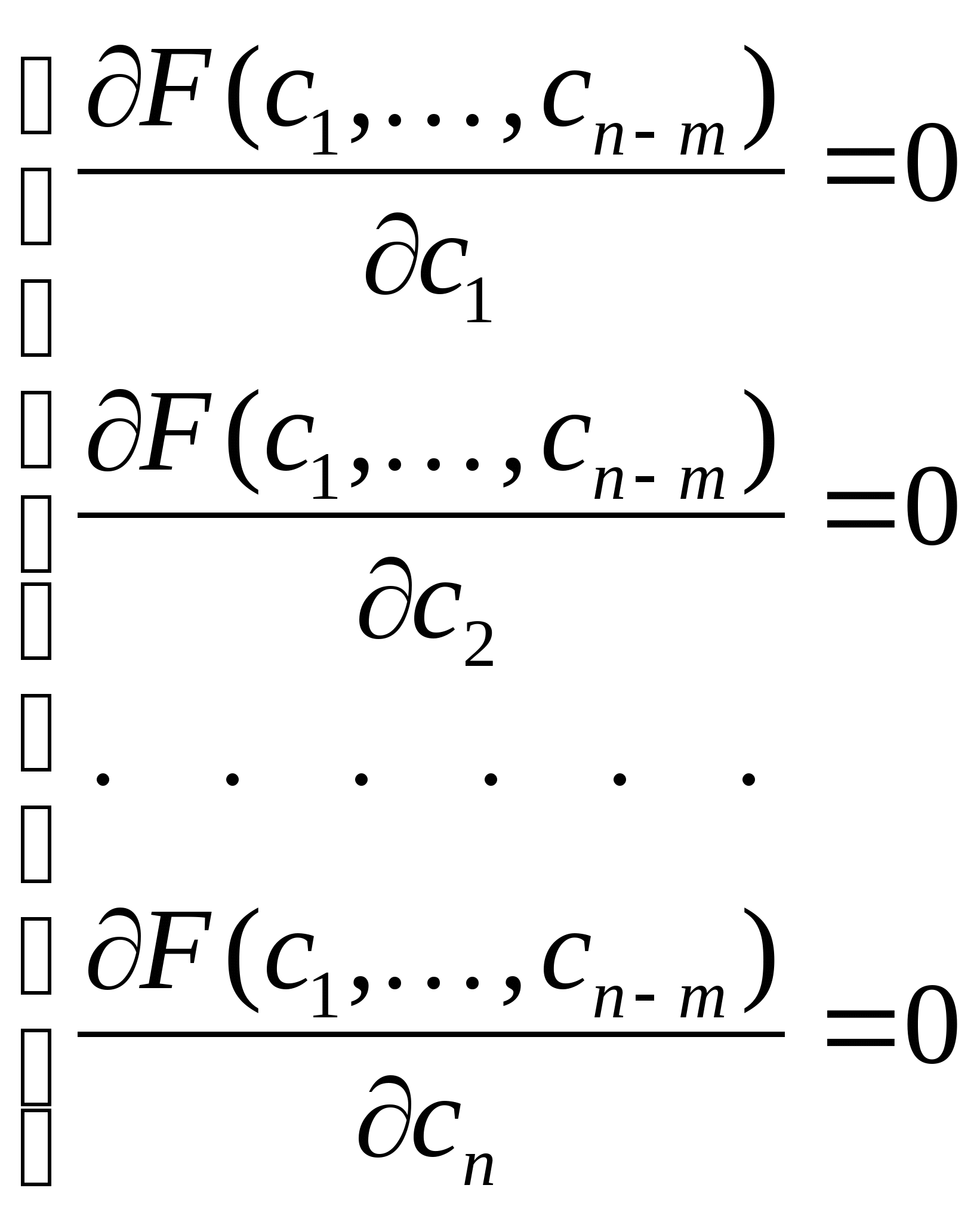
Т.к. функция является положительно определенной квадратичной функцией, то частные производные по всем переменным являются линейными функциями от этих переменных:
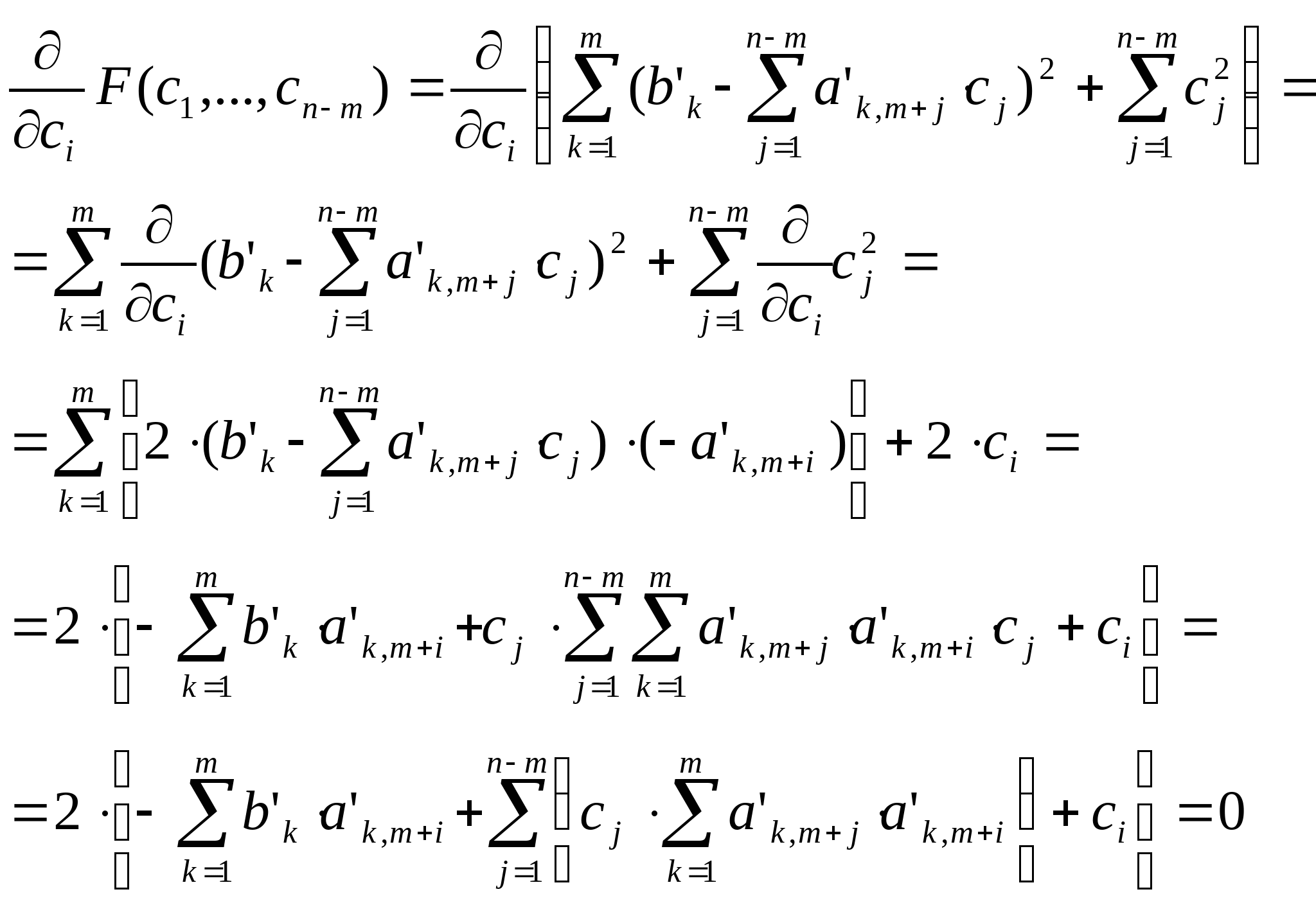
Таким образом условием минимума функции 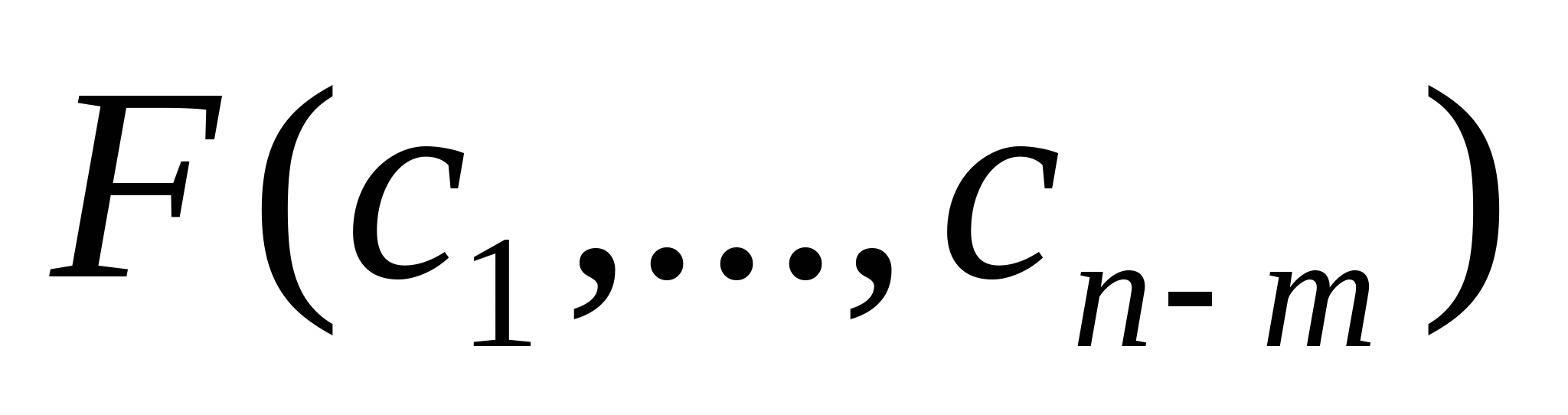 является решение системы линейных уравнений: является решение системы линейных уравнений: i = 1..n-m
| 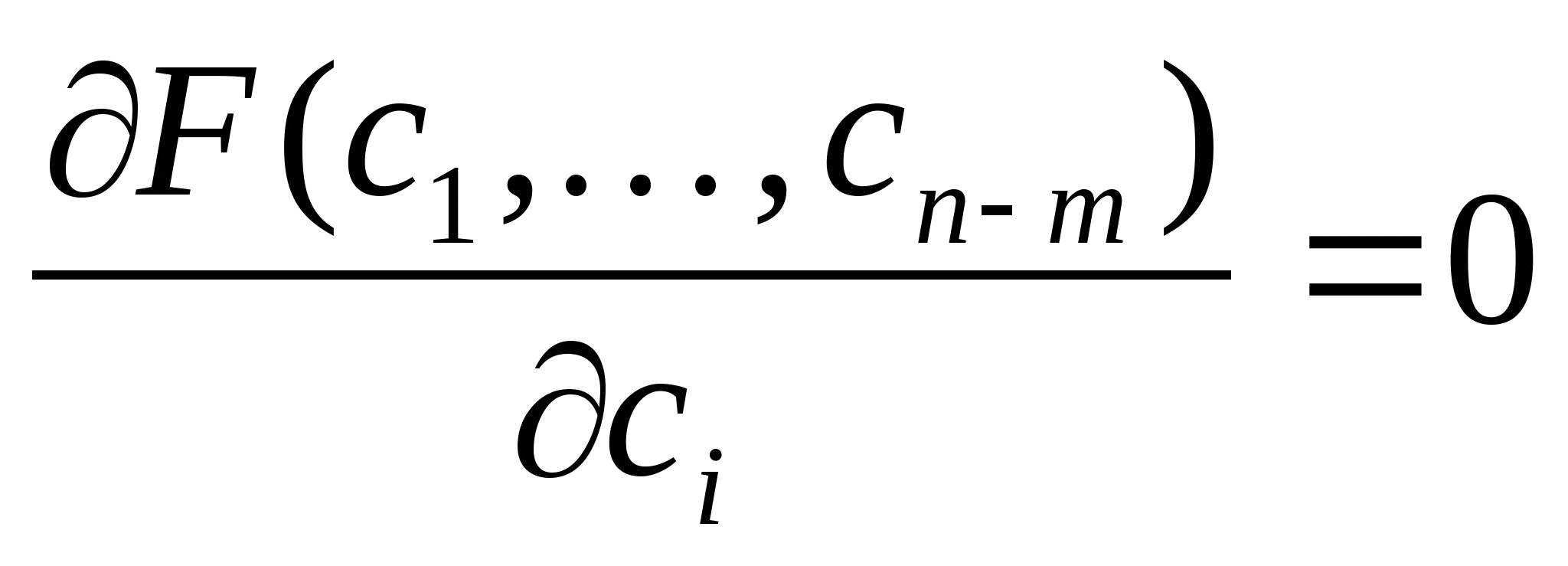
| | 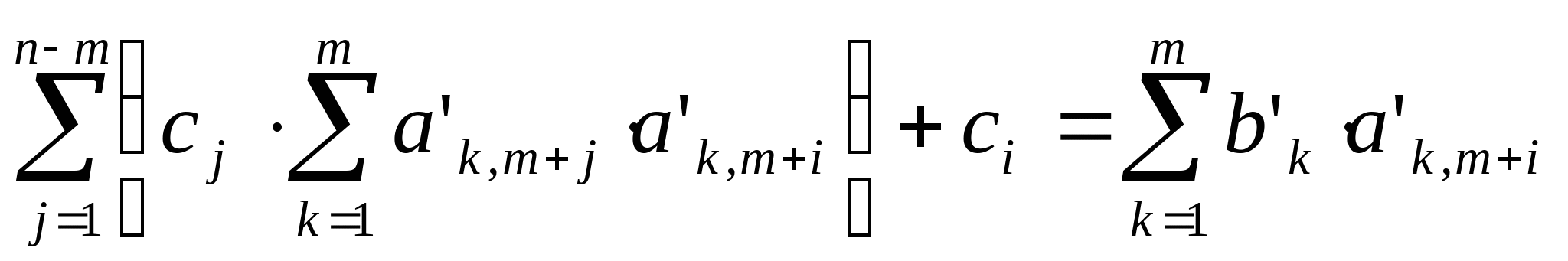
|
Построим матричную форму этой системы:
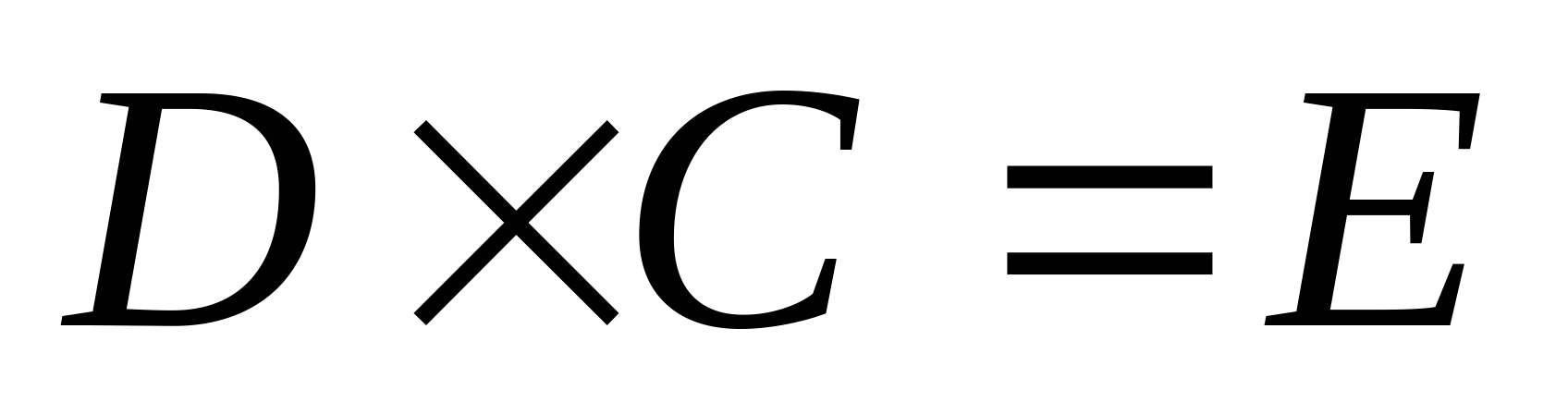
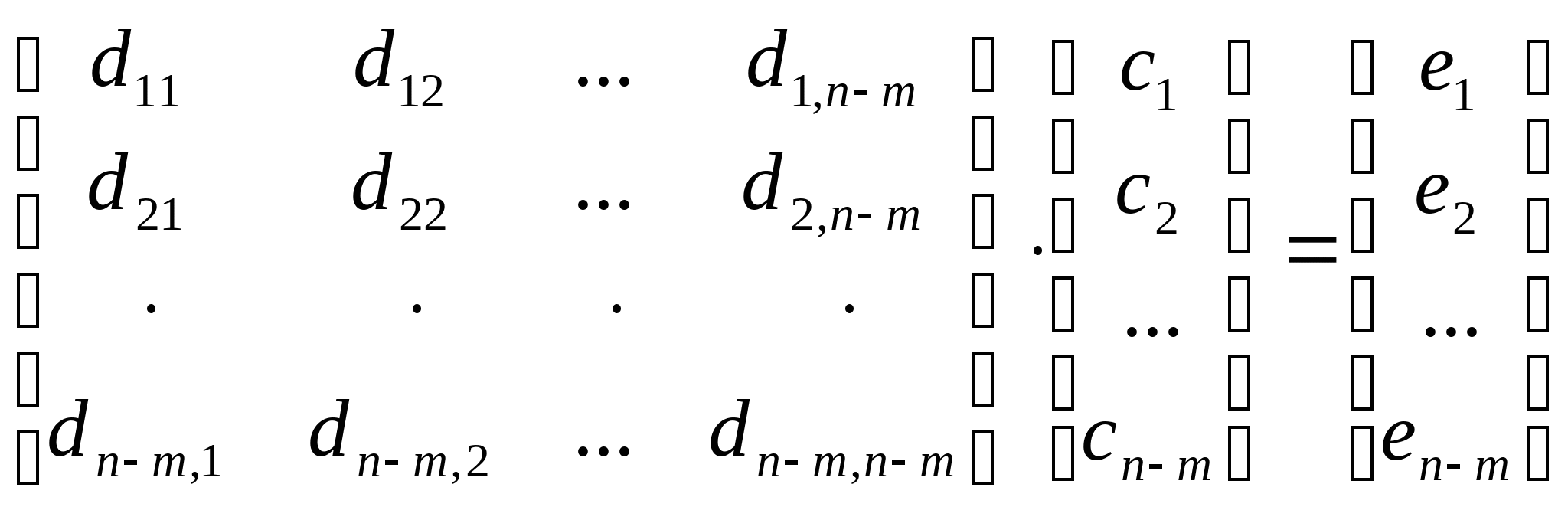
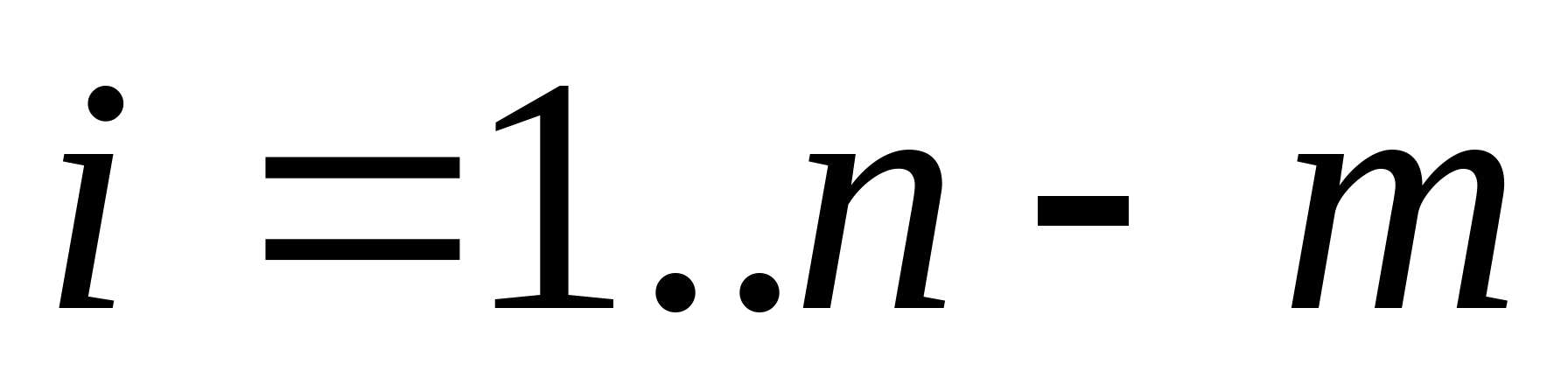
Решая эту систему получим искомое значение коэффициентов 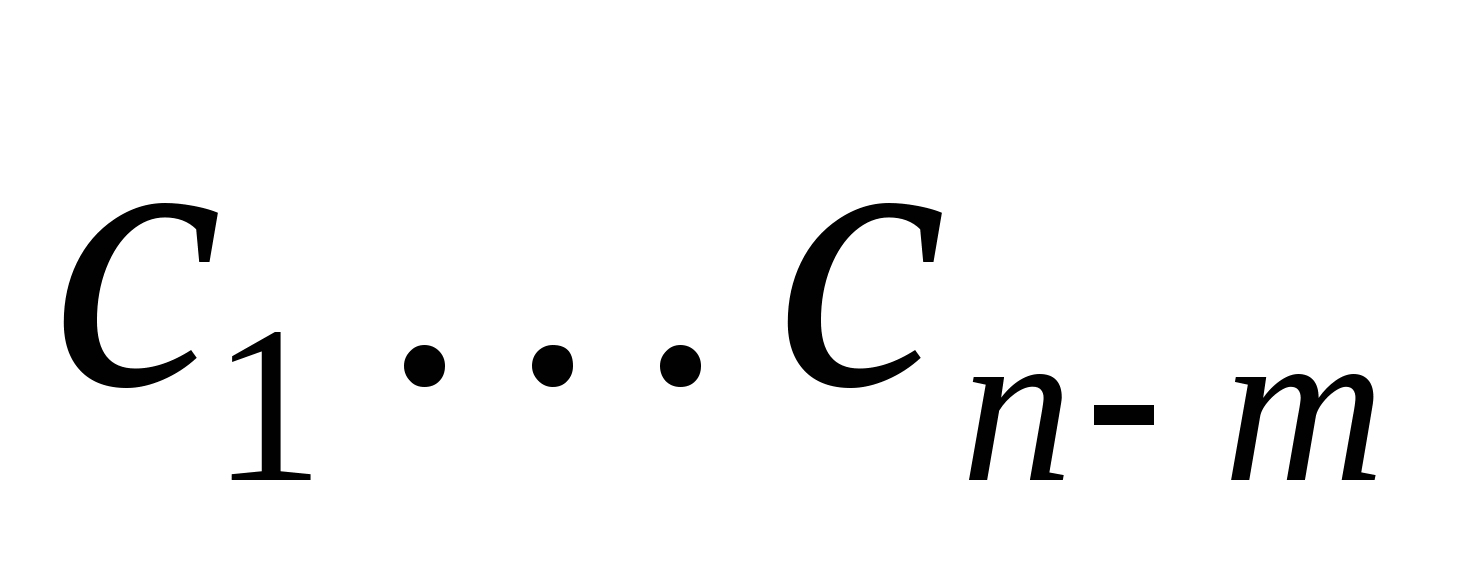 при которых вектор-решений X минимален по Евклидовой норме. при которых вектор-решений X минимален по Евклидовой норме.
В MatLab: C = E \ D;
Откуда вектор минимального по норме решения равен 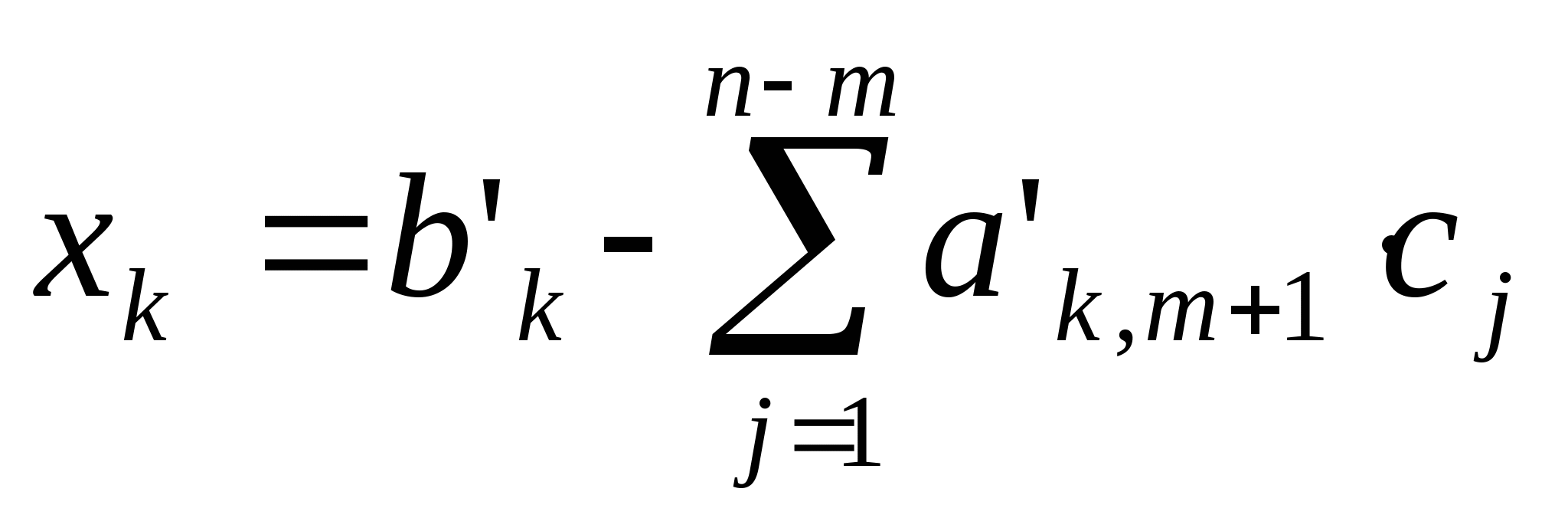 , где k = 1..m. , где k = 1..m.
Пример1 (Ex1.m)
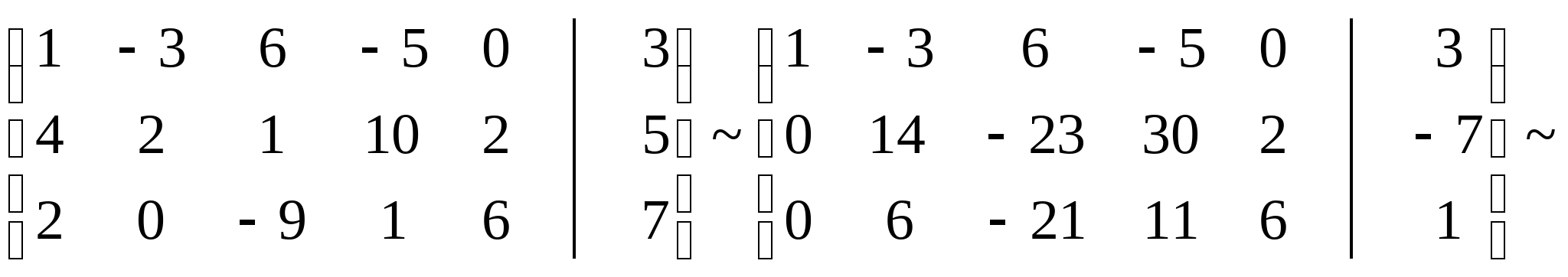 
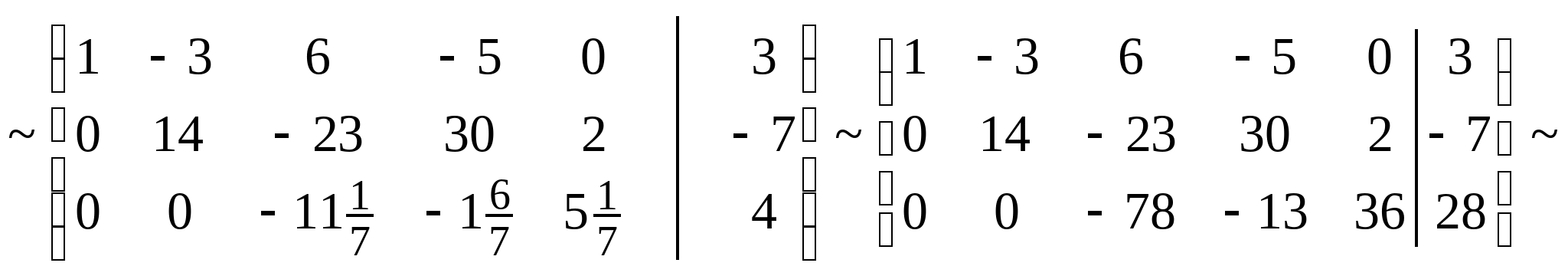 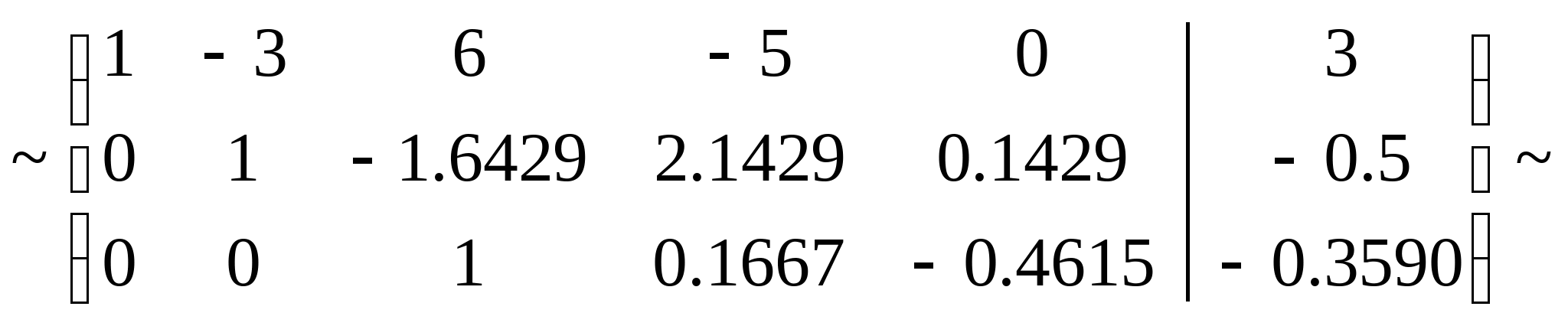


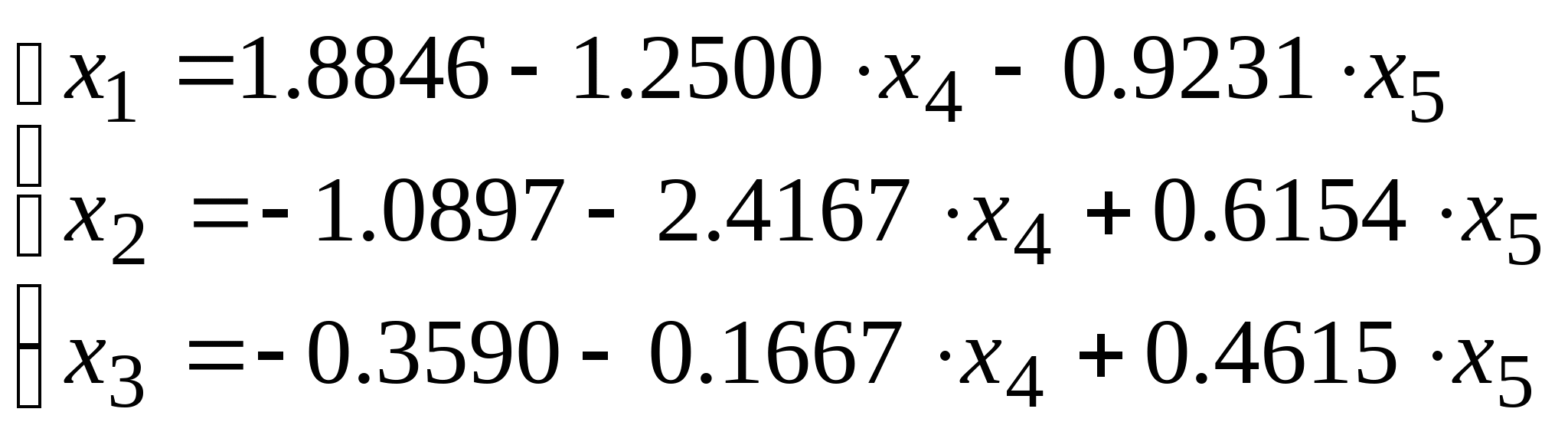
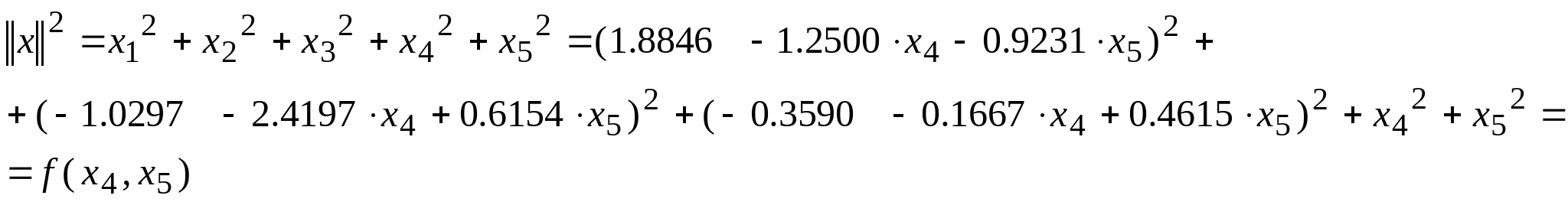 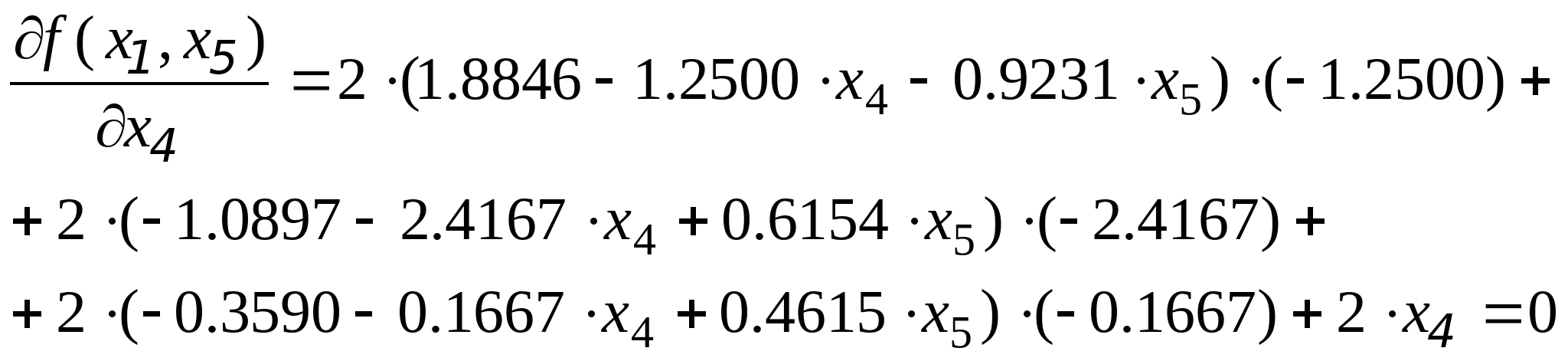
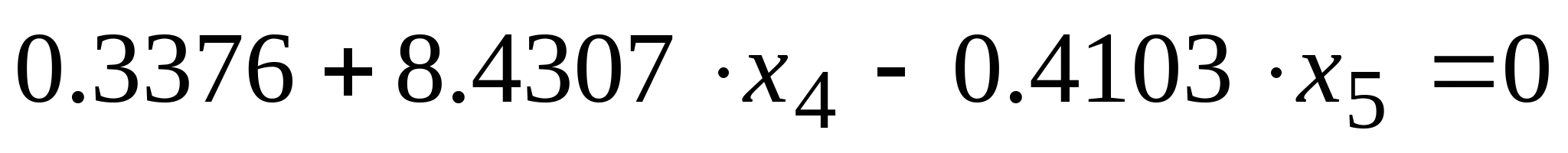
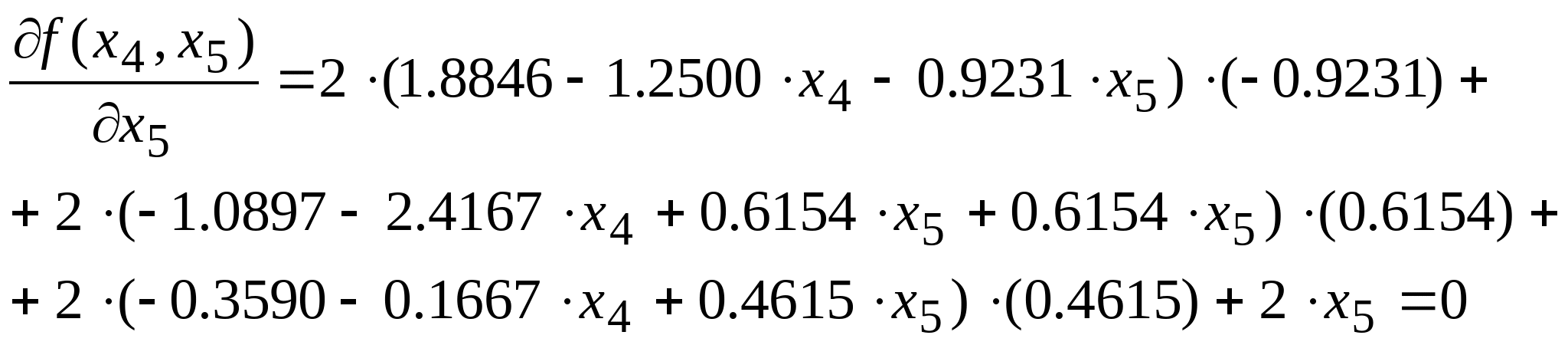
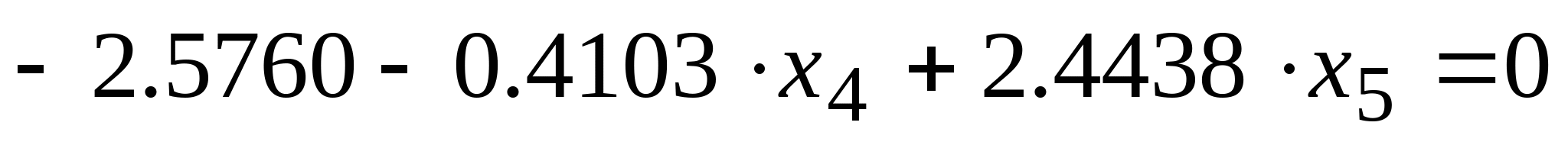
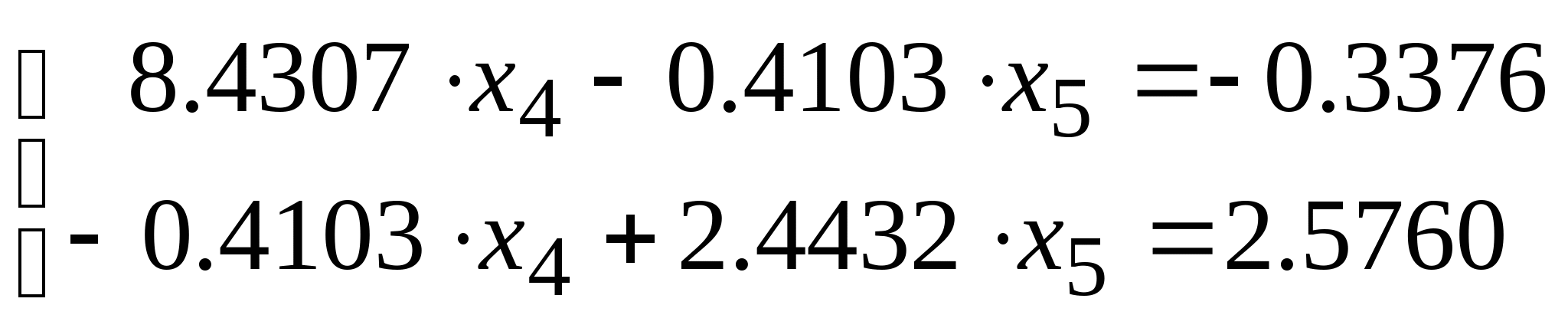
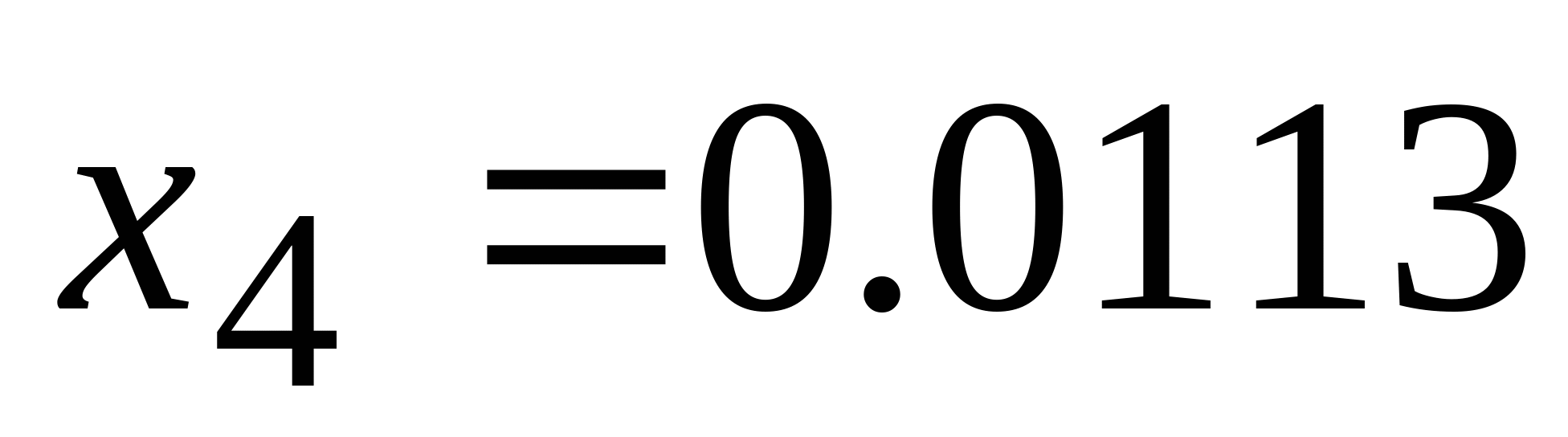
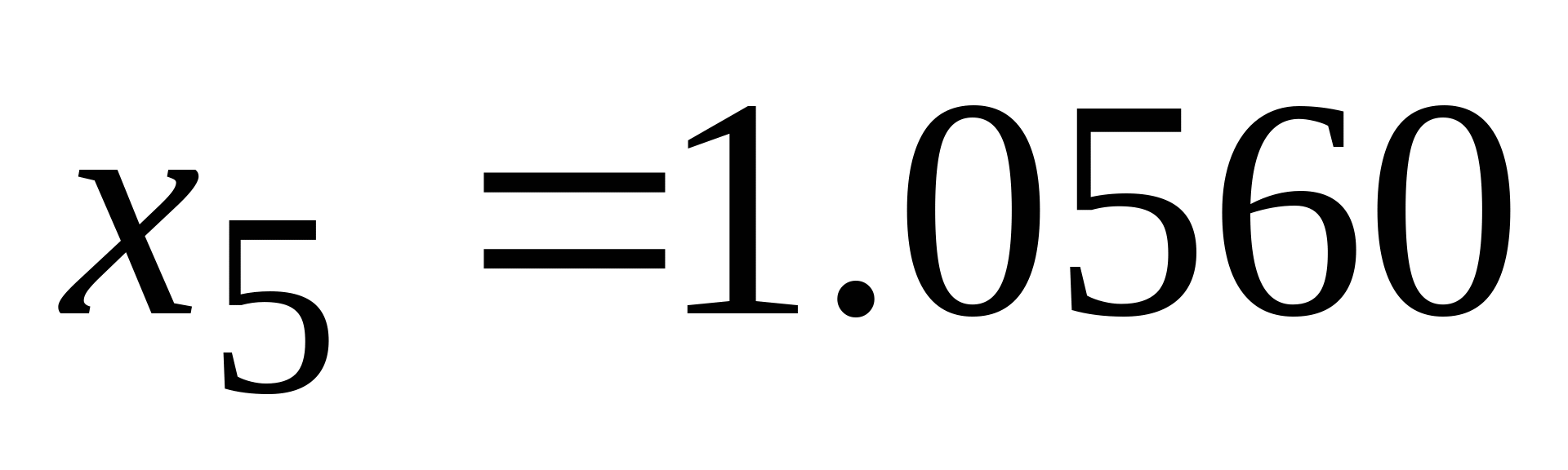
| Вектор решения
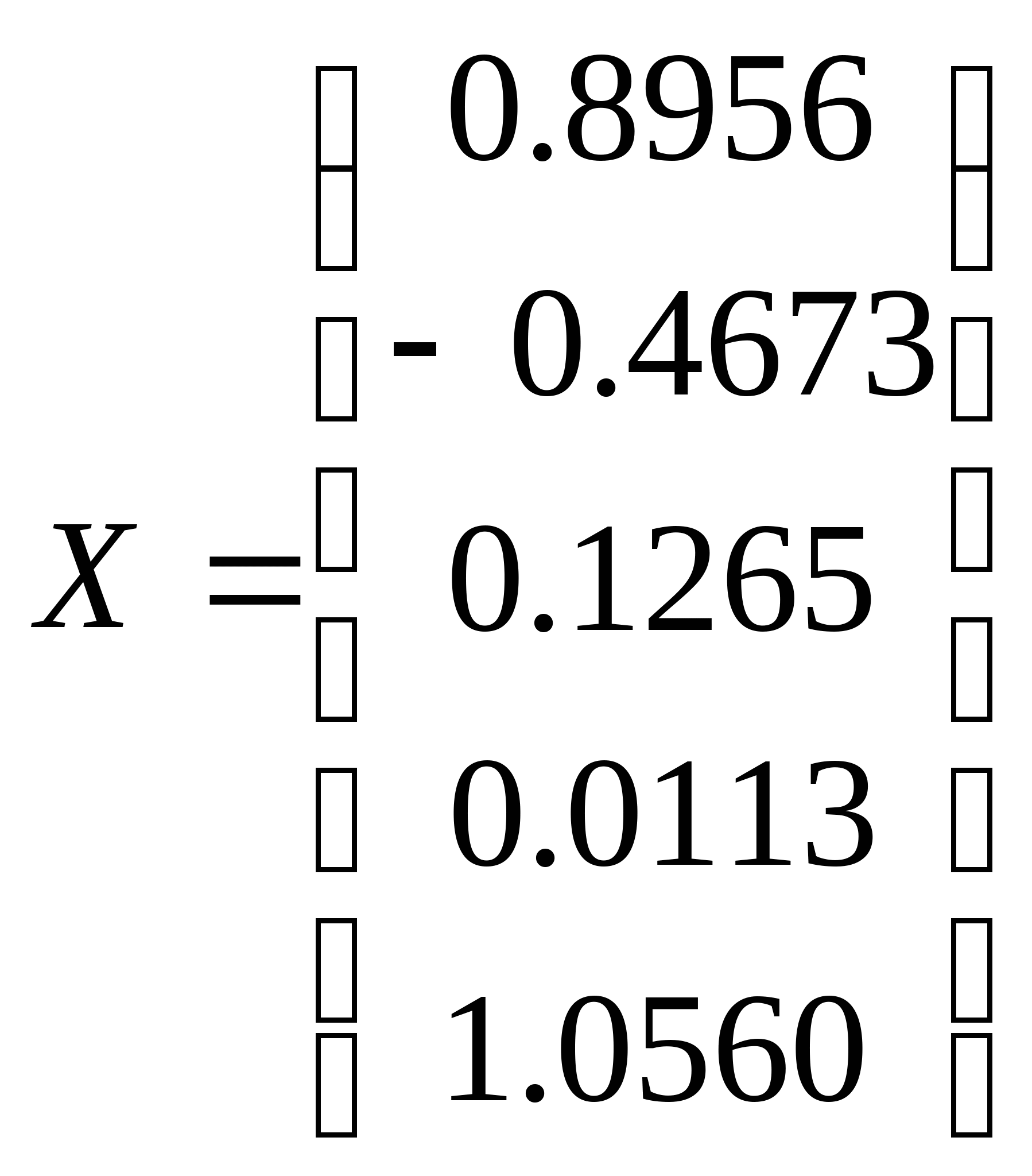
| Норма вектора решений
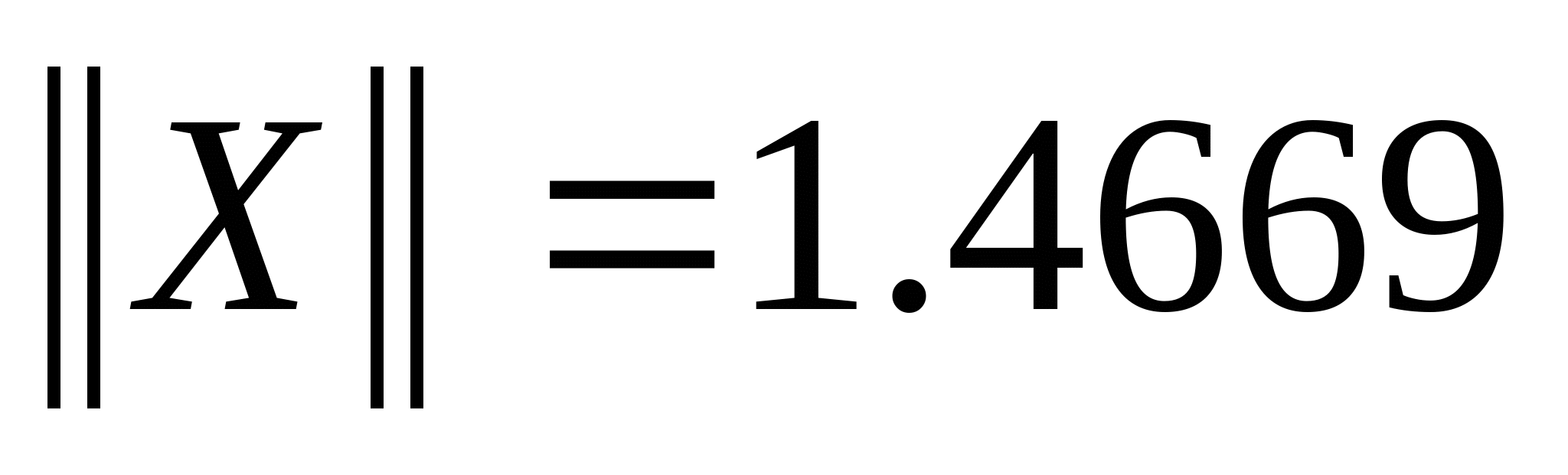
| Невязка
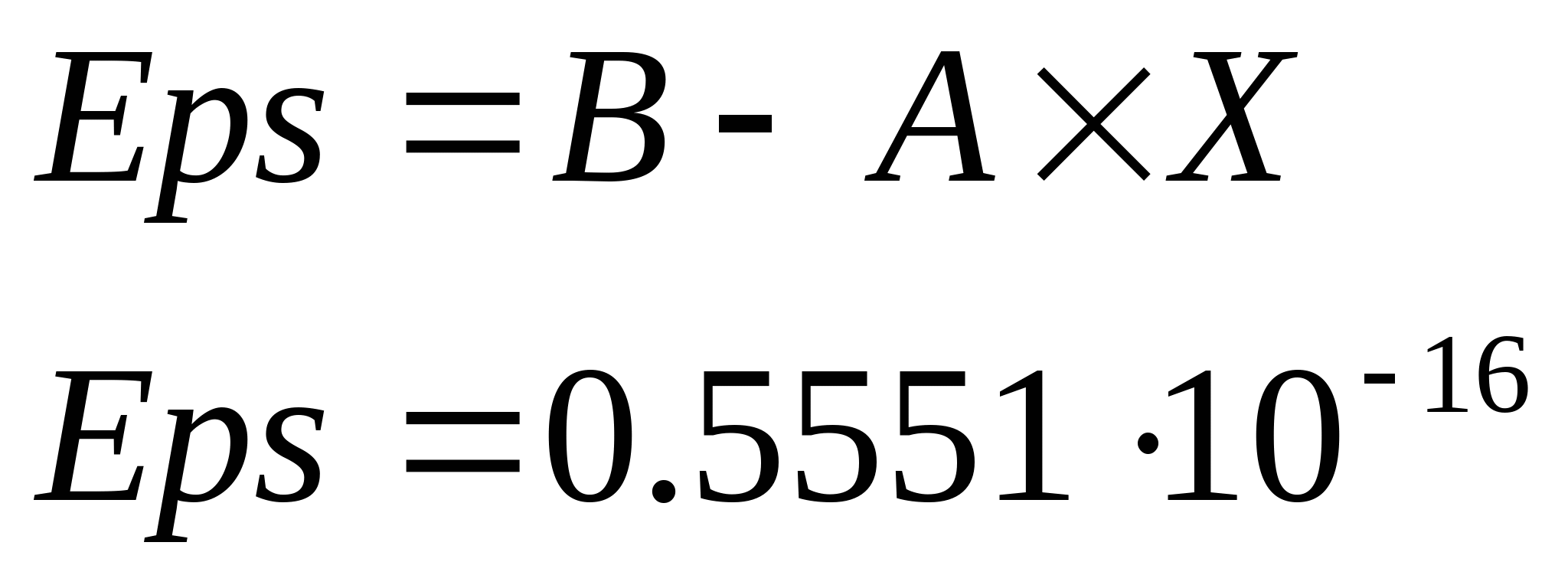
|
Пример 10.
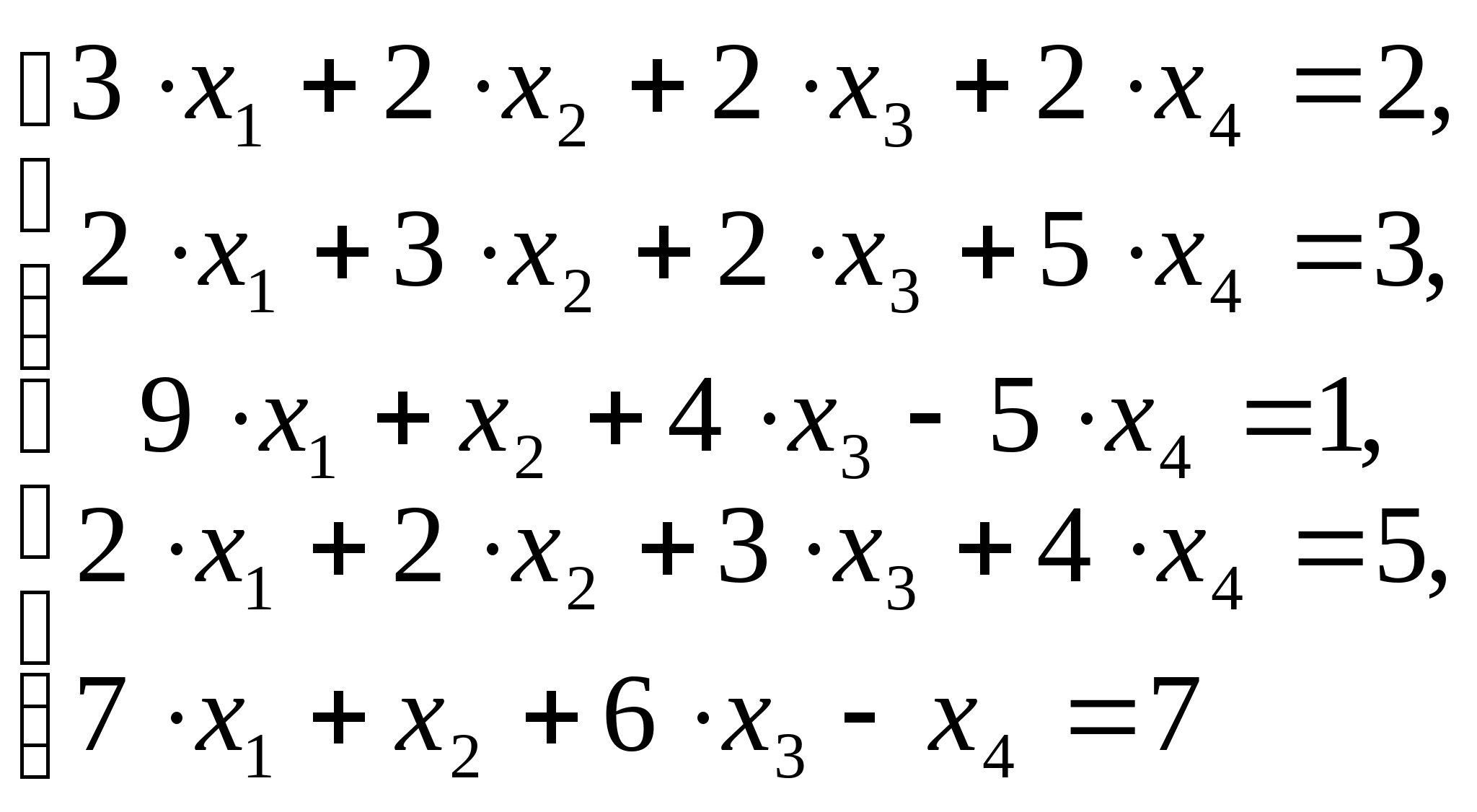
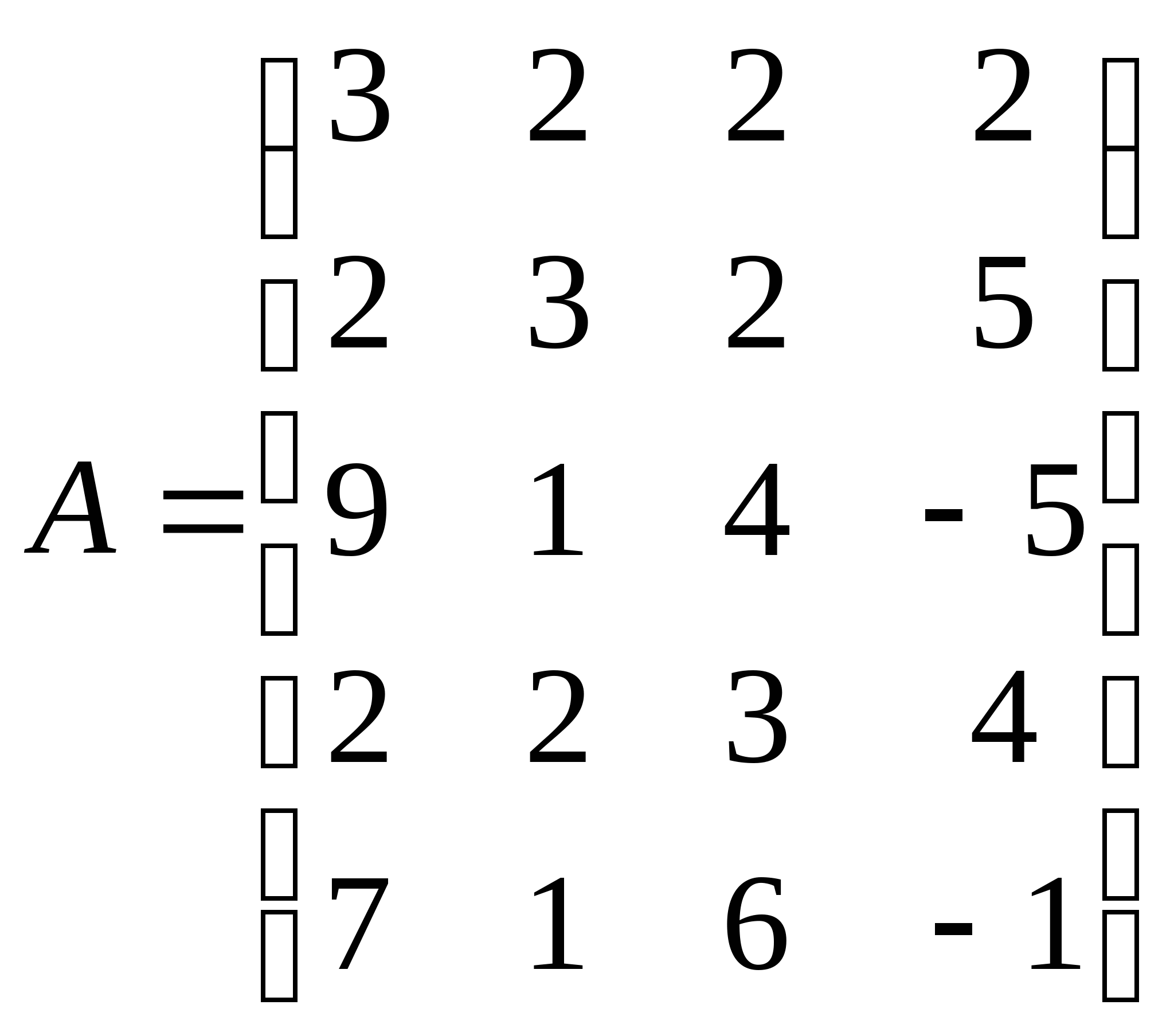 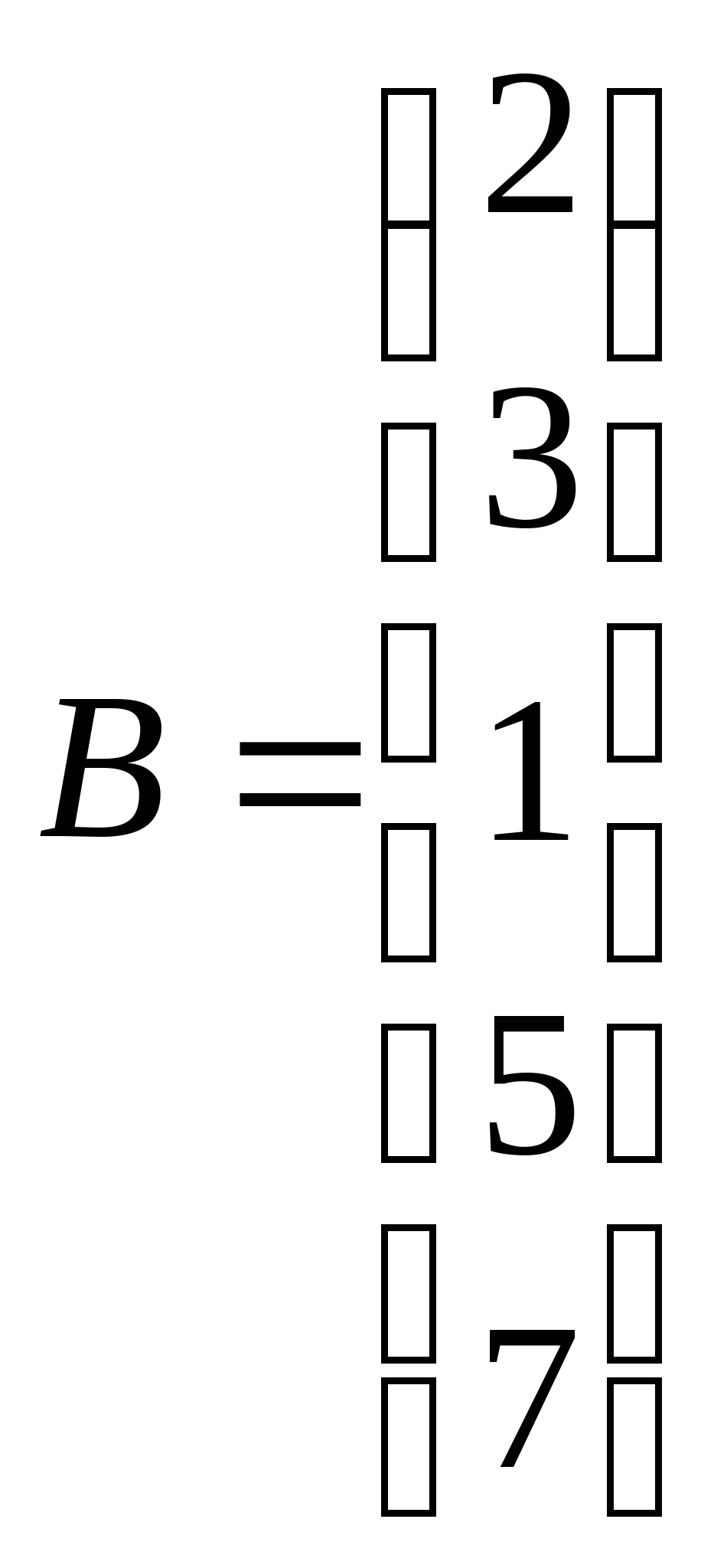
Расширенная матрица системы:

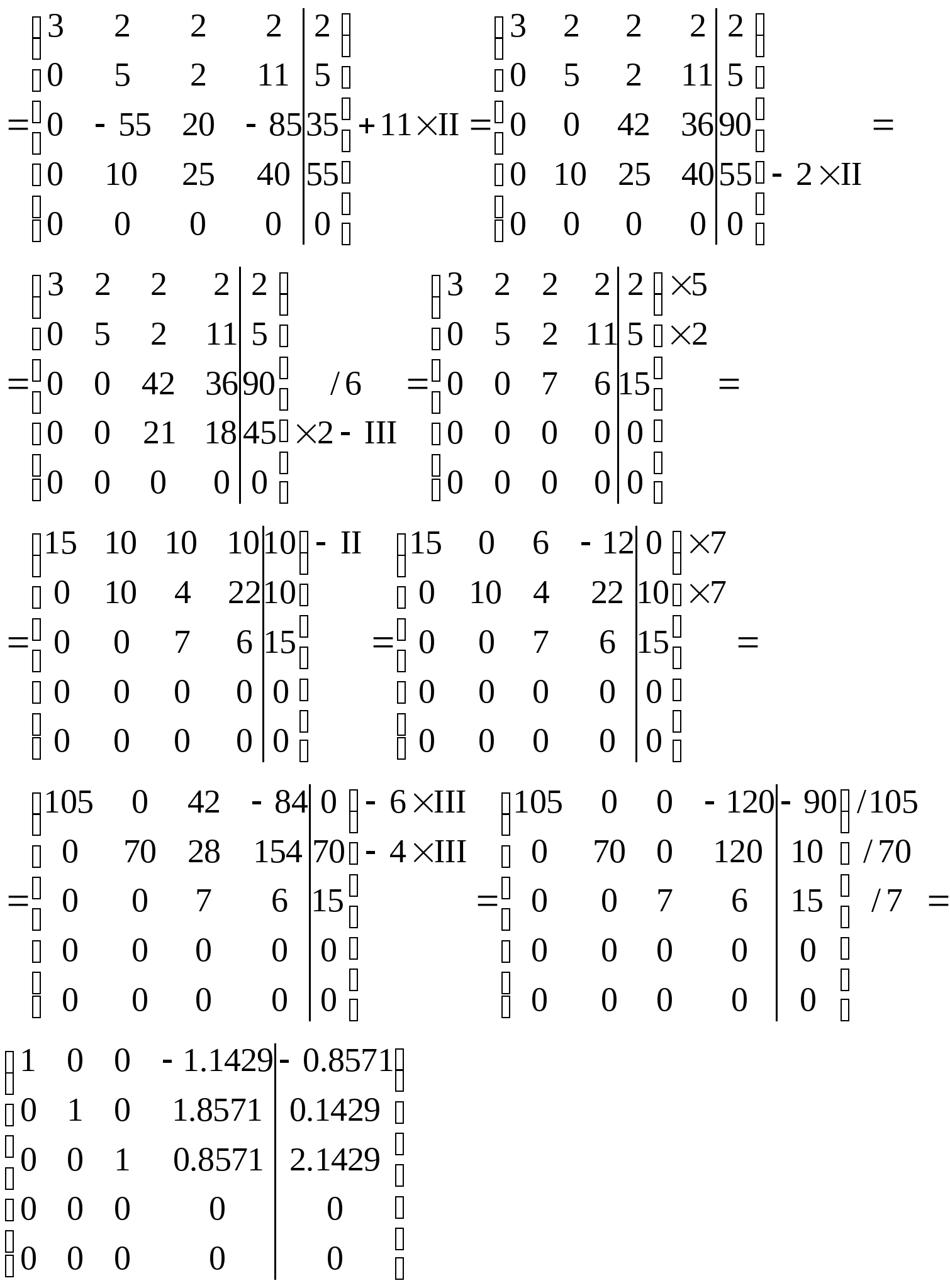
Получили диагональную матрицу. Откуда
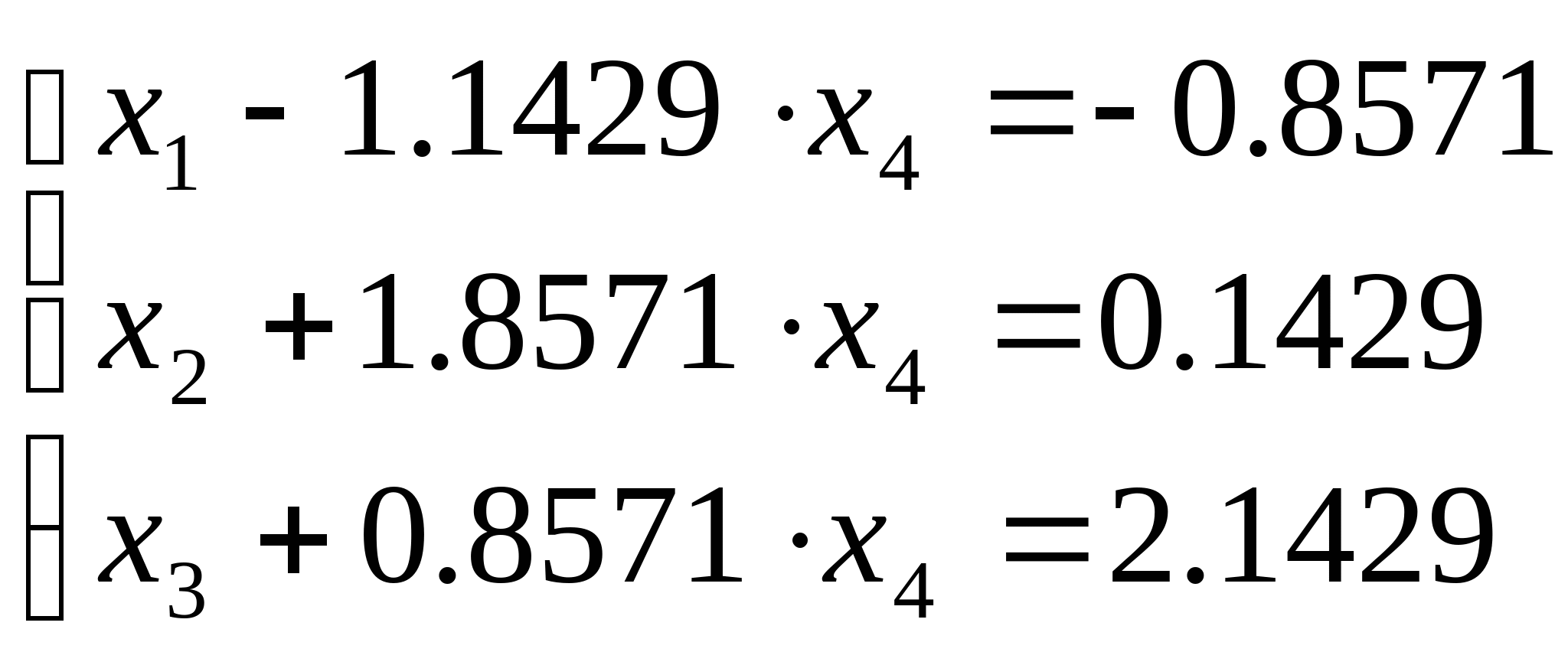
При 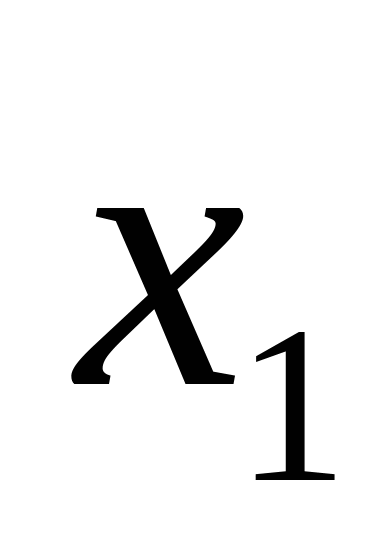 = =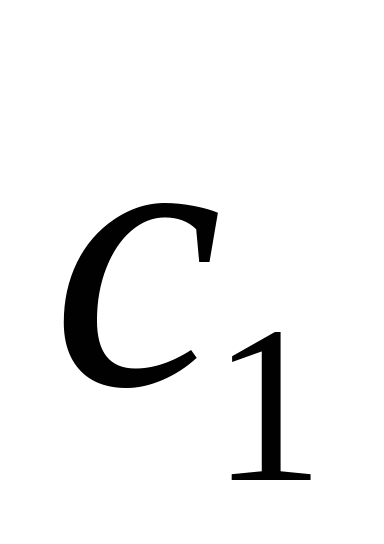 общее решение системы имеет вид: общее решение системы имеет вид:
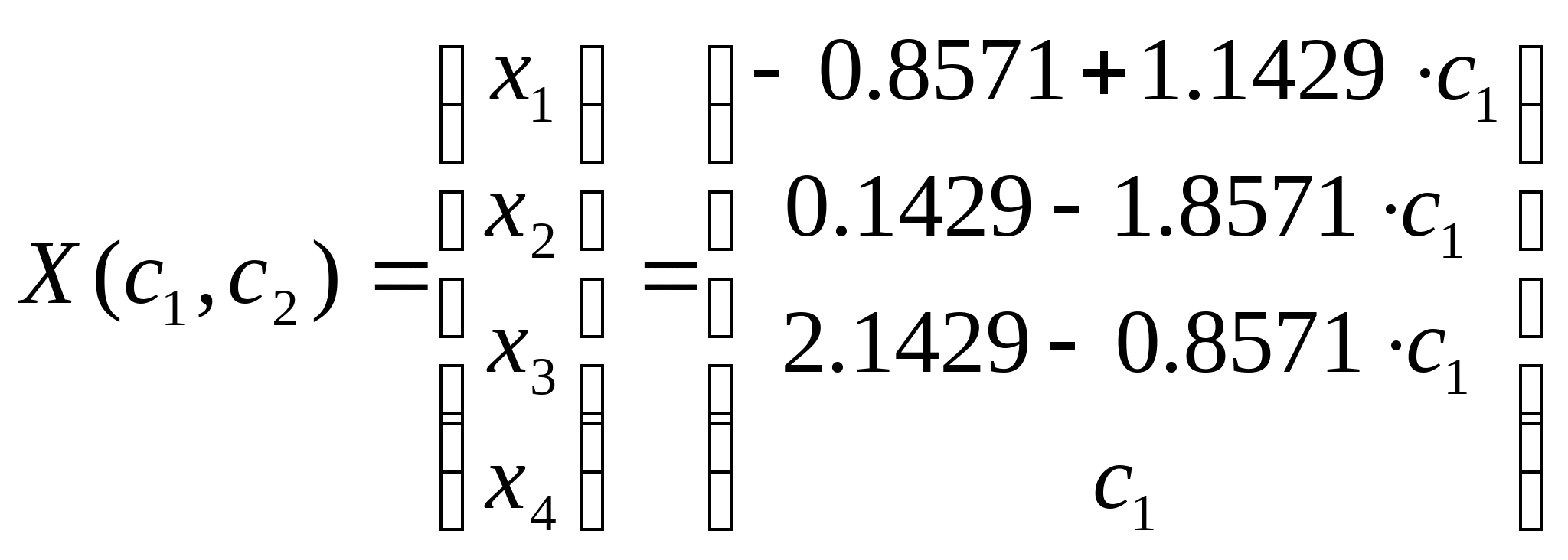
Для нахождения минимальных решений составим функцию и найдём её производную:
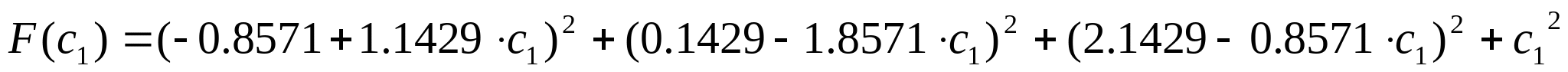
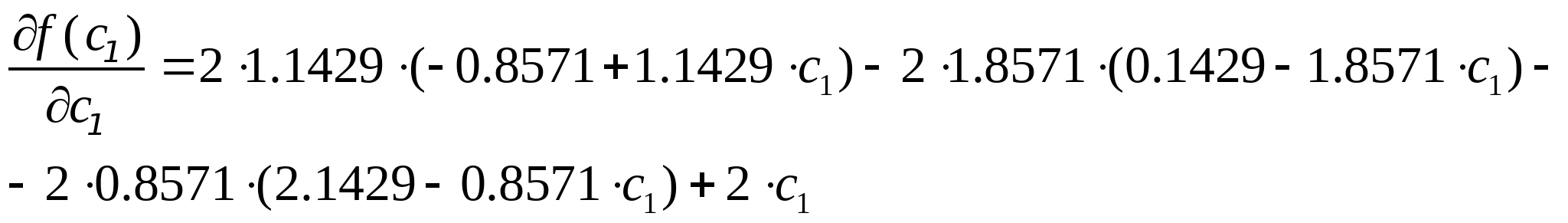 Приравнивая производную к нулю получим линейное уравнение, откуда найдём точку в которых F минимальна: Приравнивая производную к нулю получим линейное уравнение, откуда найдём точку в которых F минимальна:
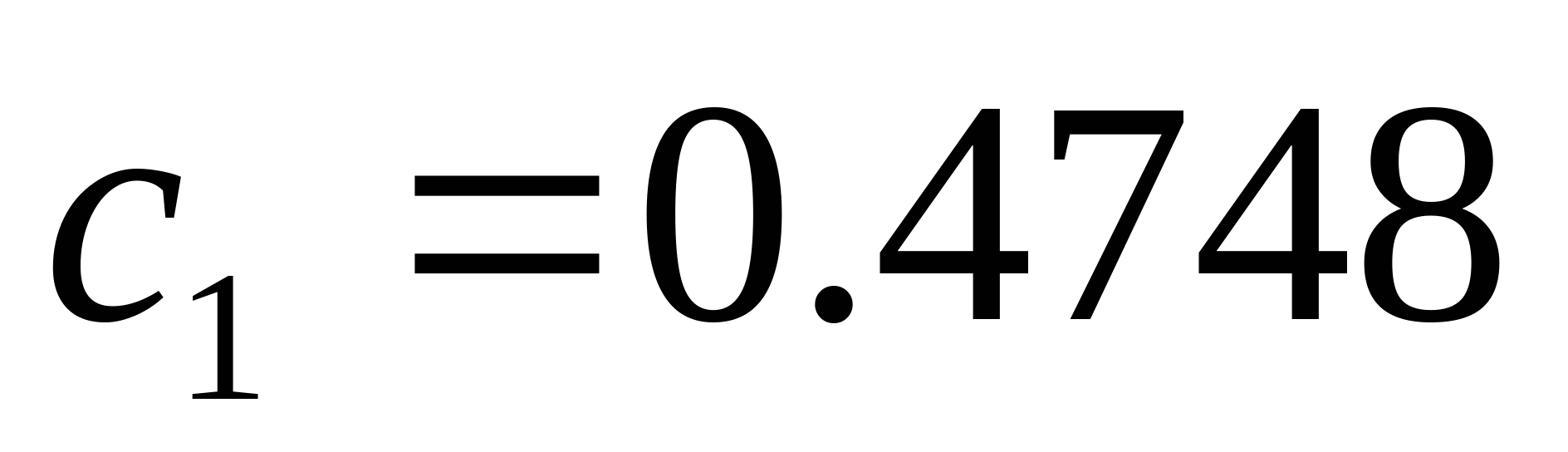
Тогда
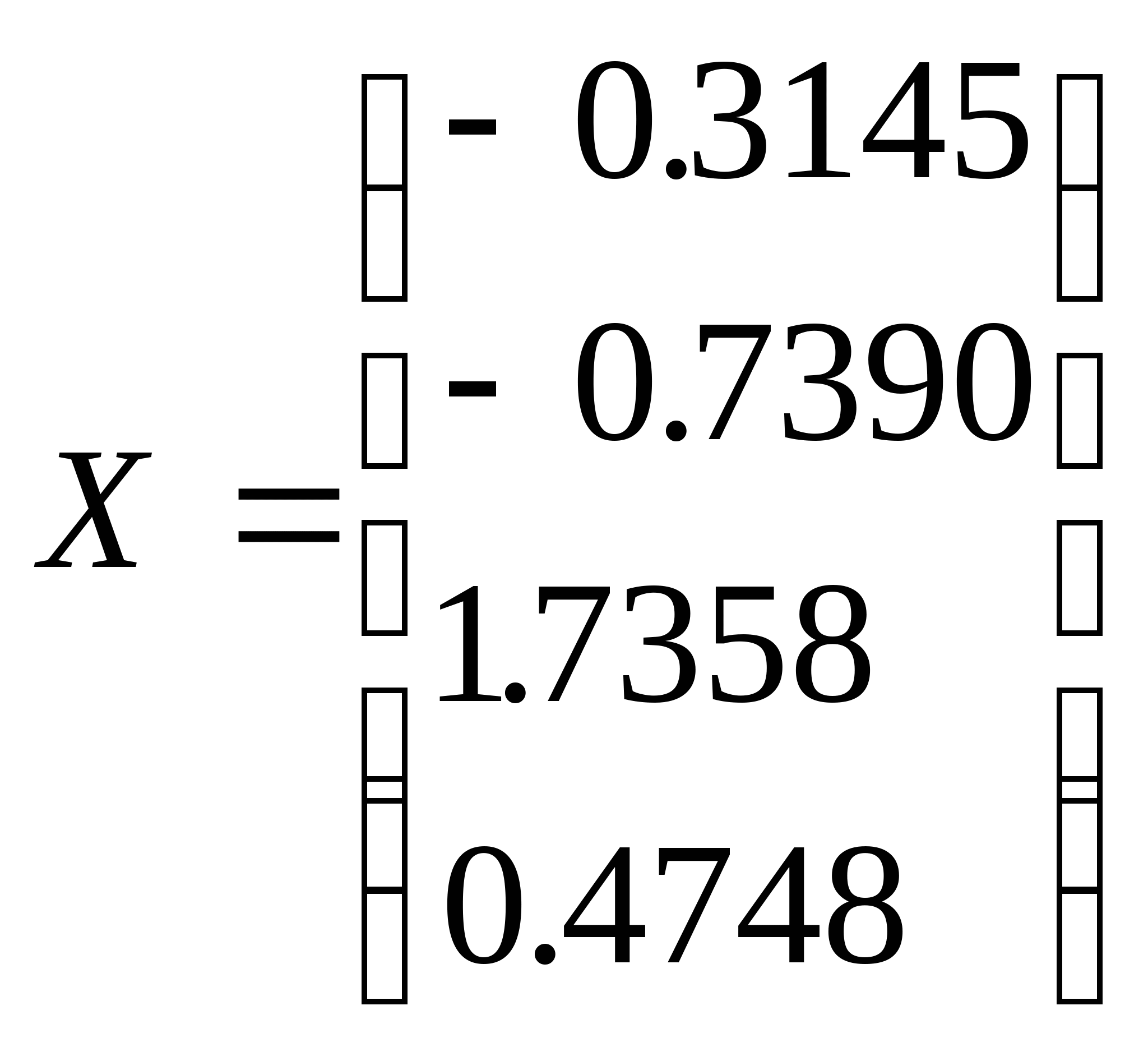 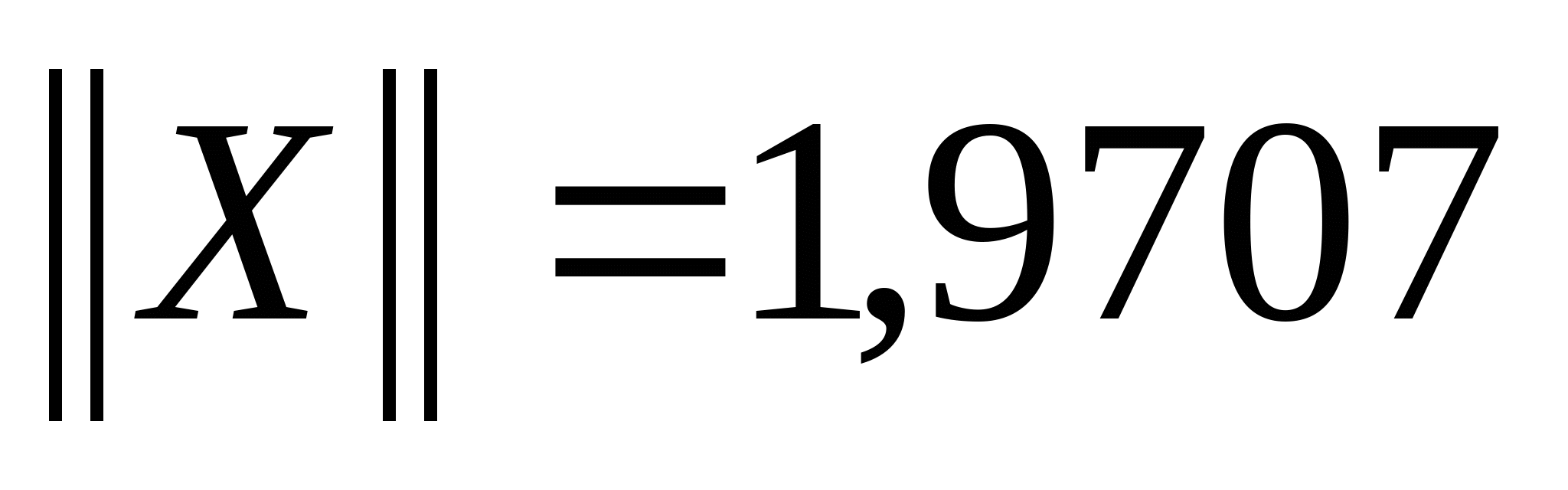 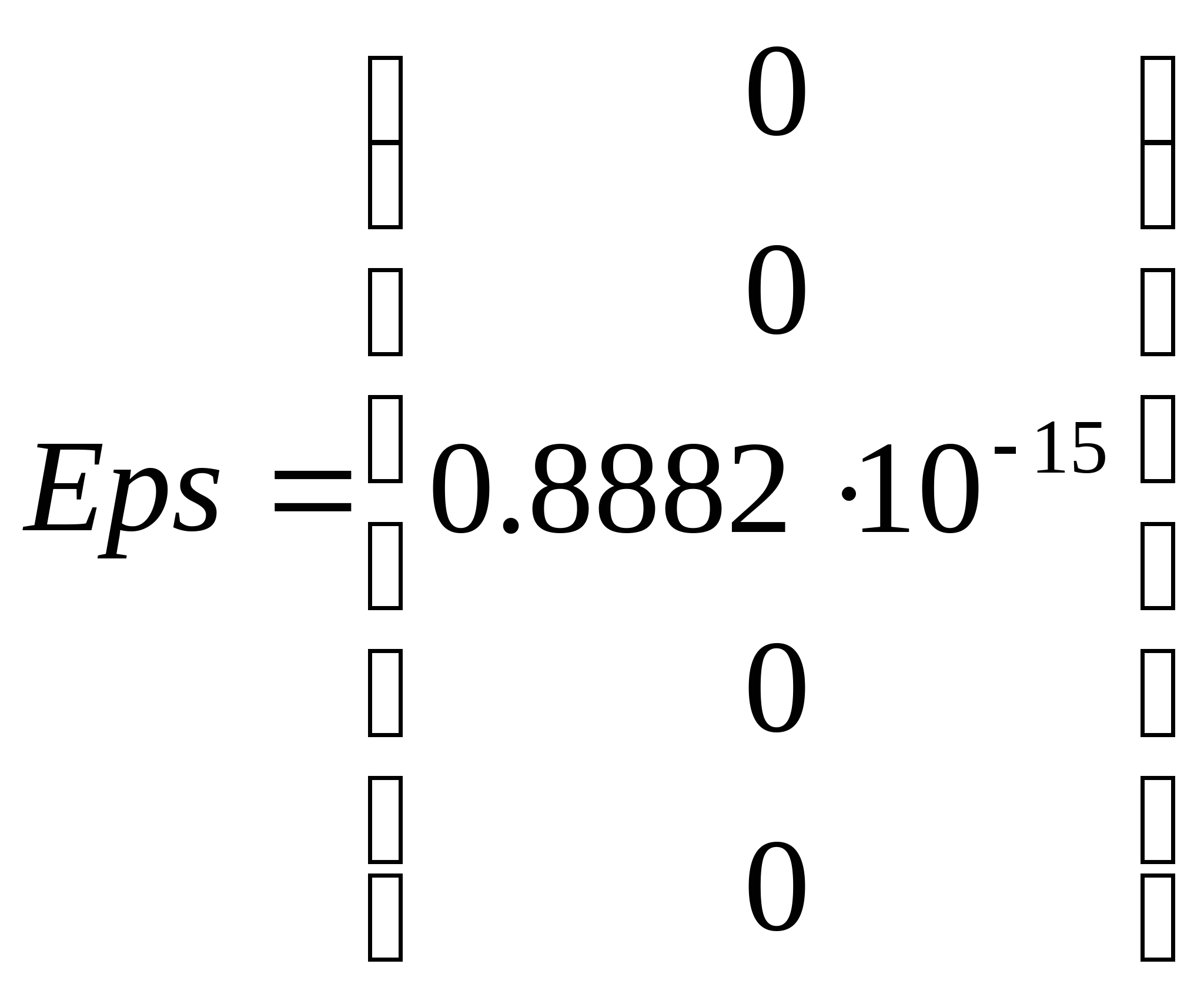
Пример 2.
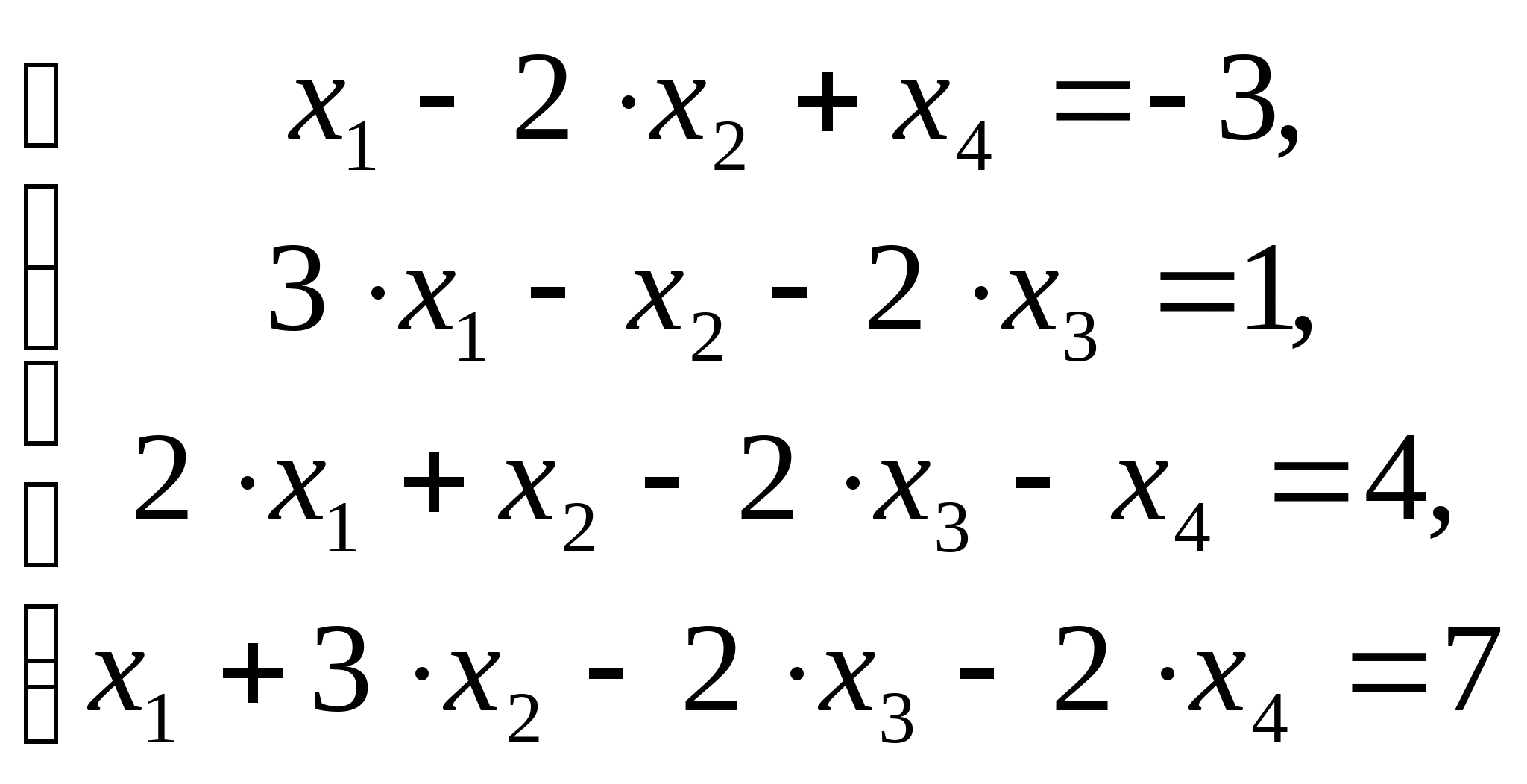
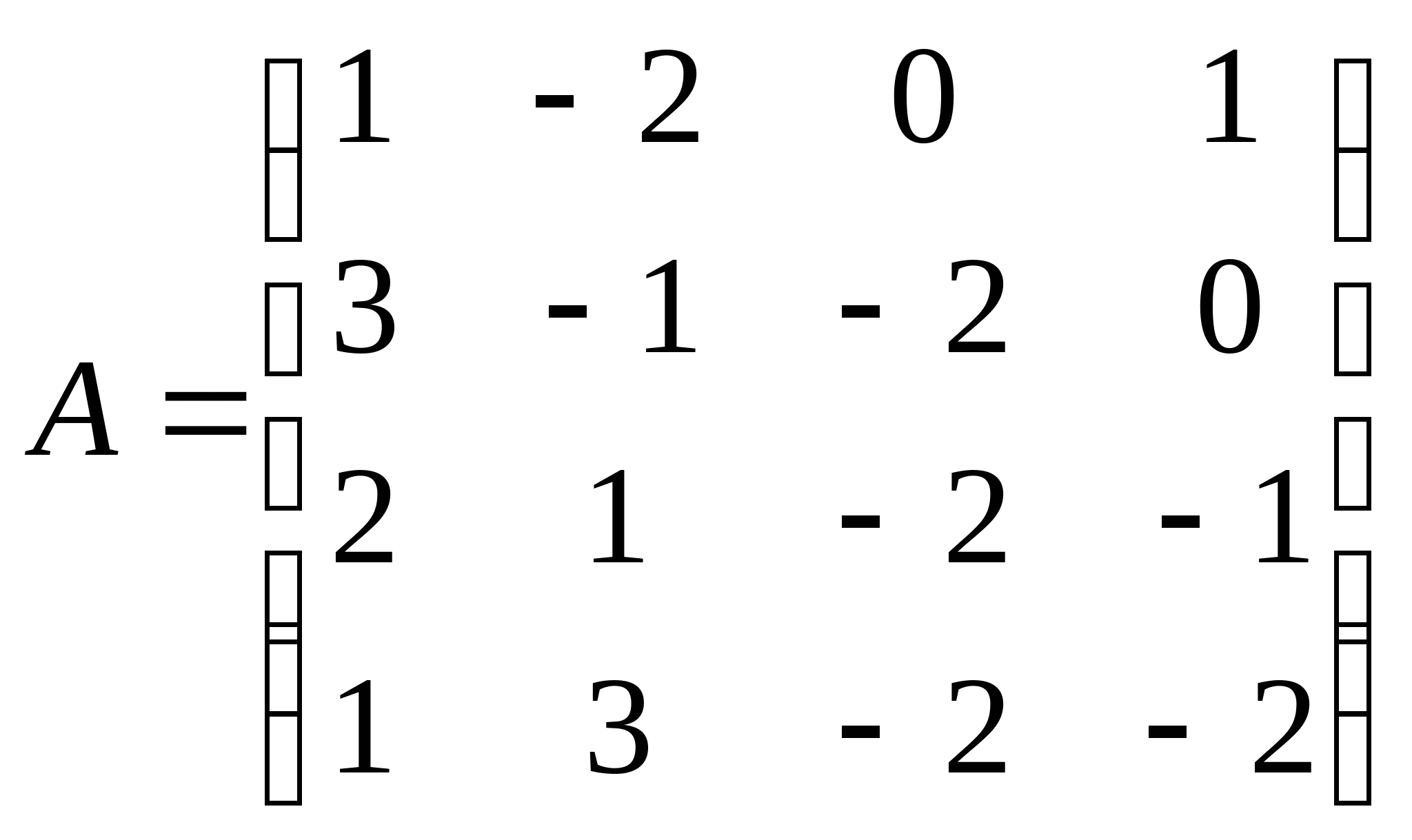 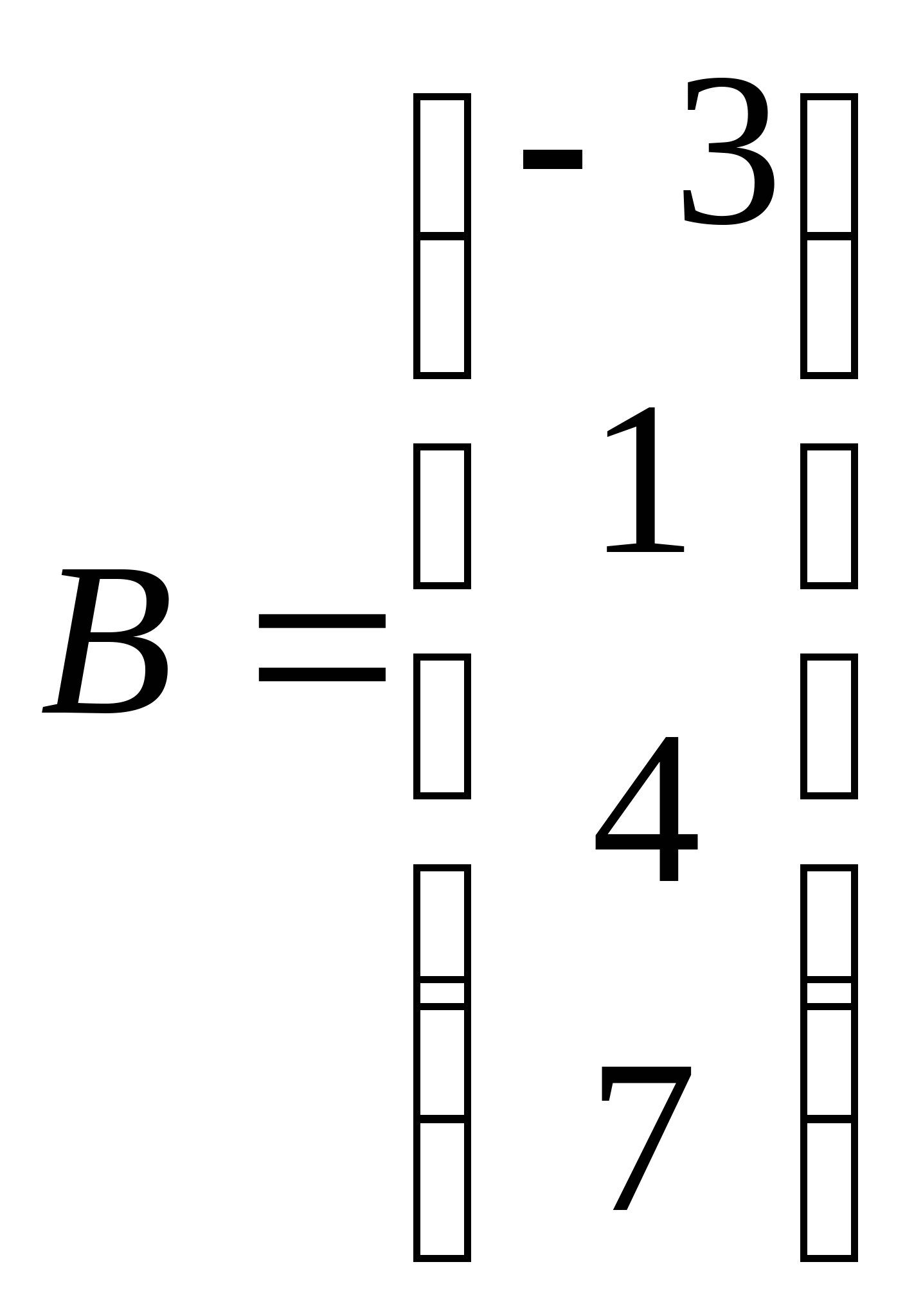
Расширенная матрица системы:
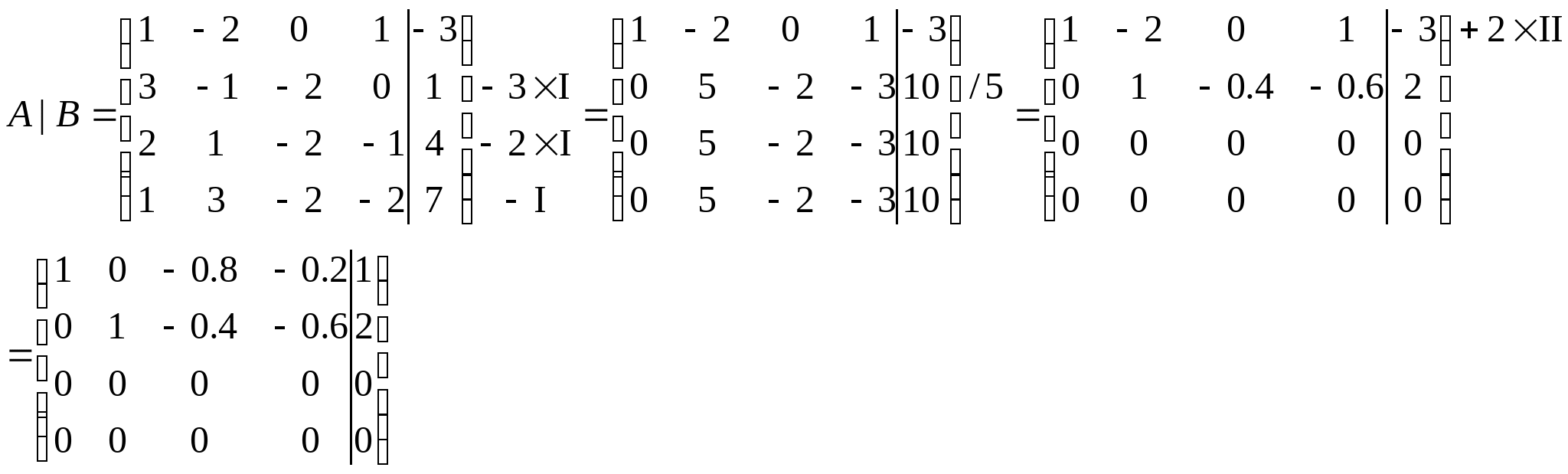
Получили диагональную матрицу. Откуда общее решение
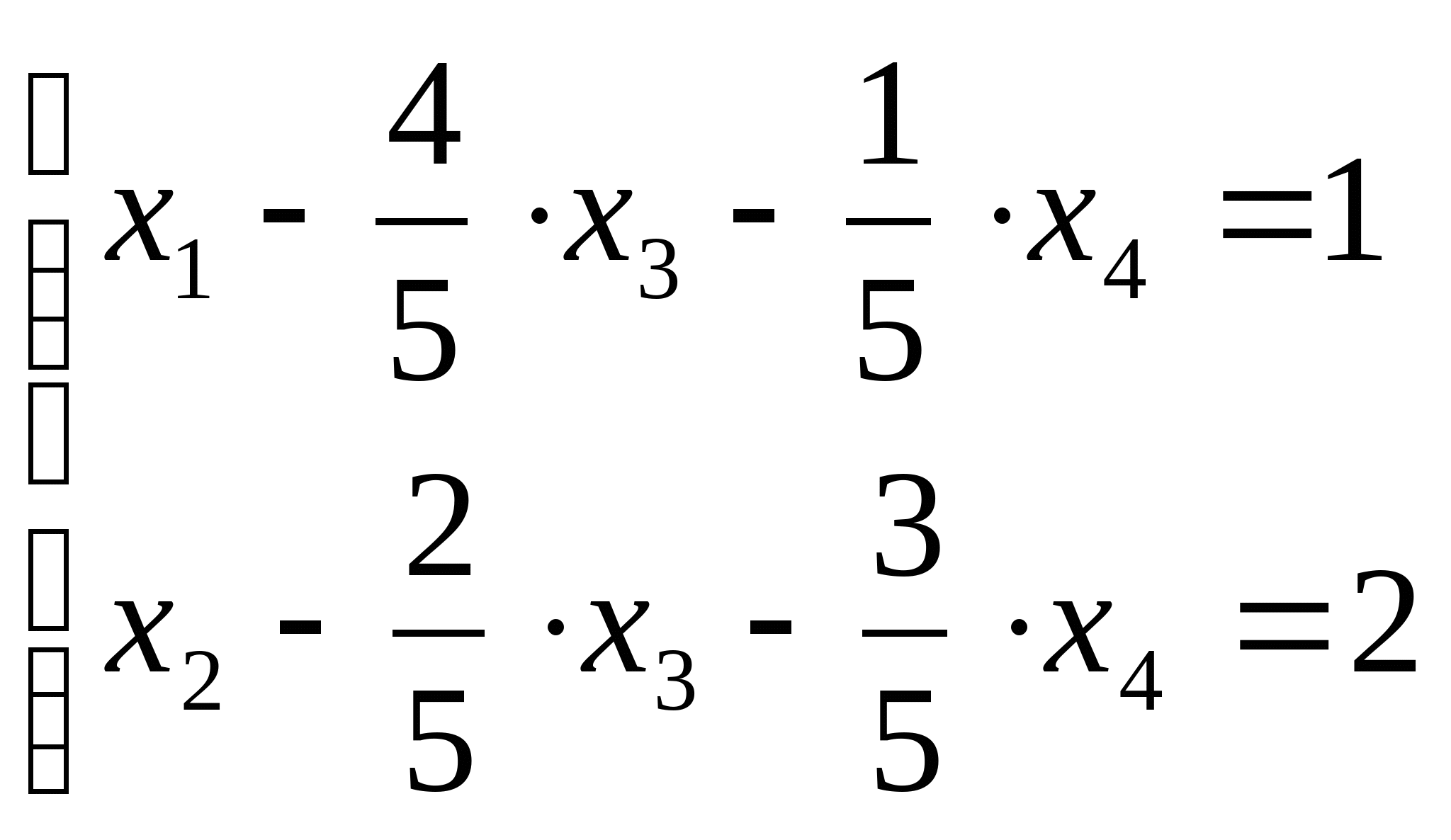
При 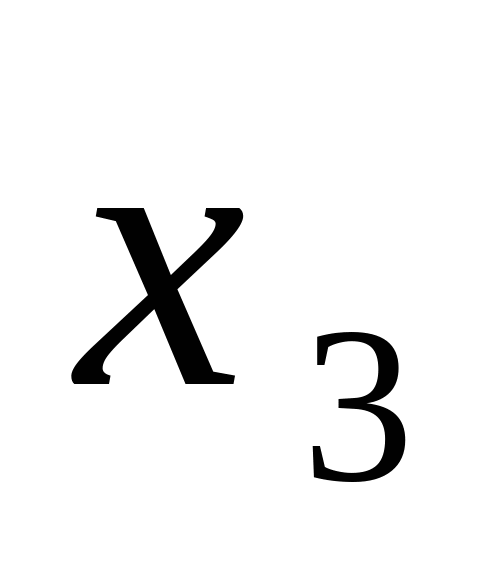 = =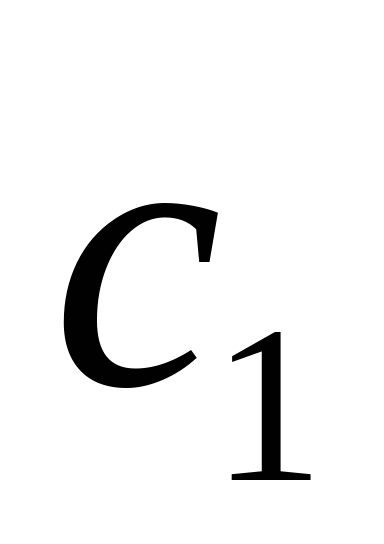 , и , и 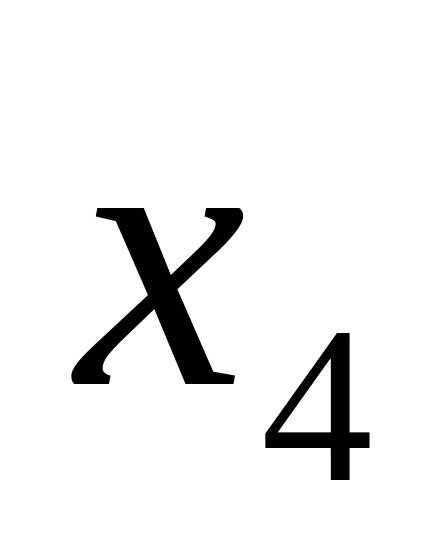 = =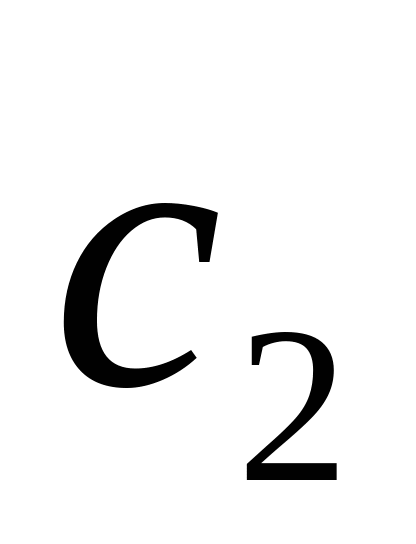 , Частное решение системы имеет вид: , Частное решение системы имеет вид:
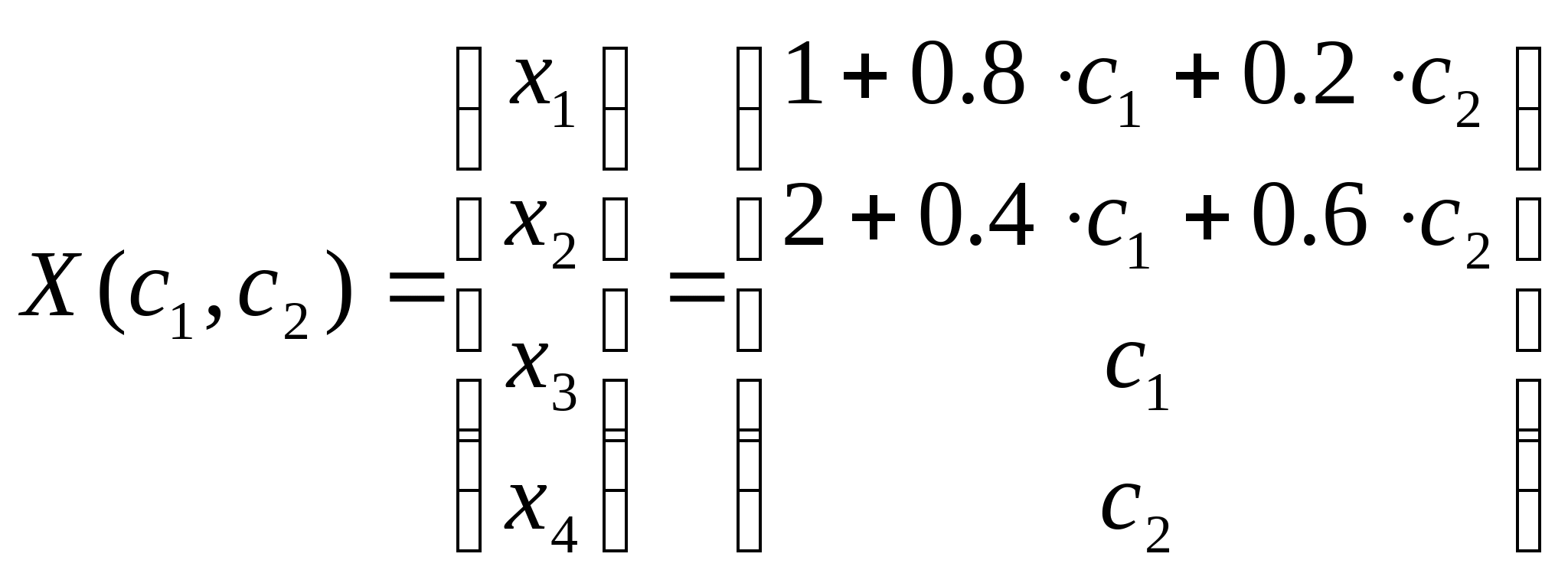
Для нахождения минимальных решений составим функцию и найдём её частные производные:
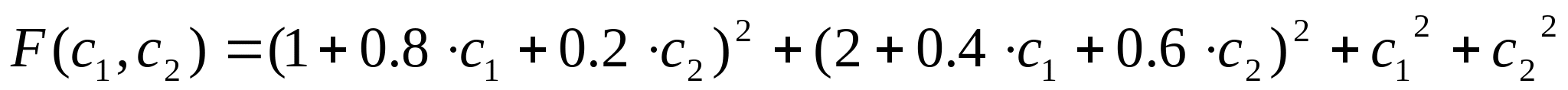
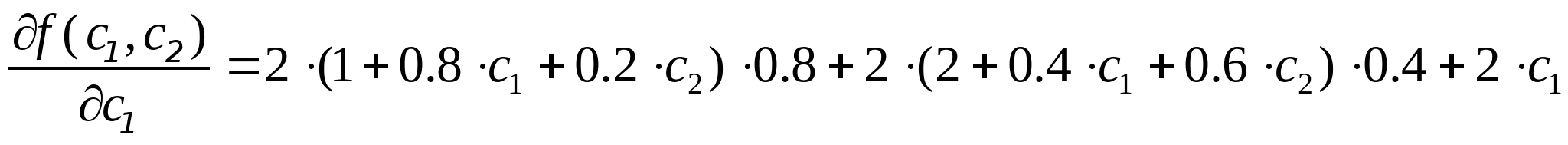 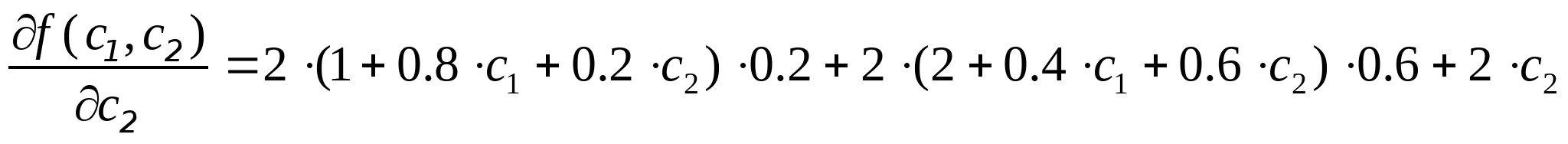 Приравнивая производные к нулю получим систему уравнений, откуда найдём точки в которых F минимальна: Приравнивая производные к нулю получим систему уравнений, откуда найдём точки в которых F минимальна:
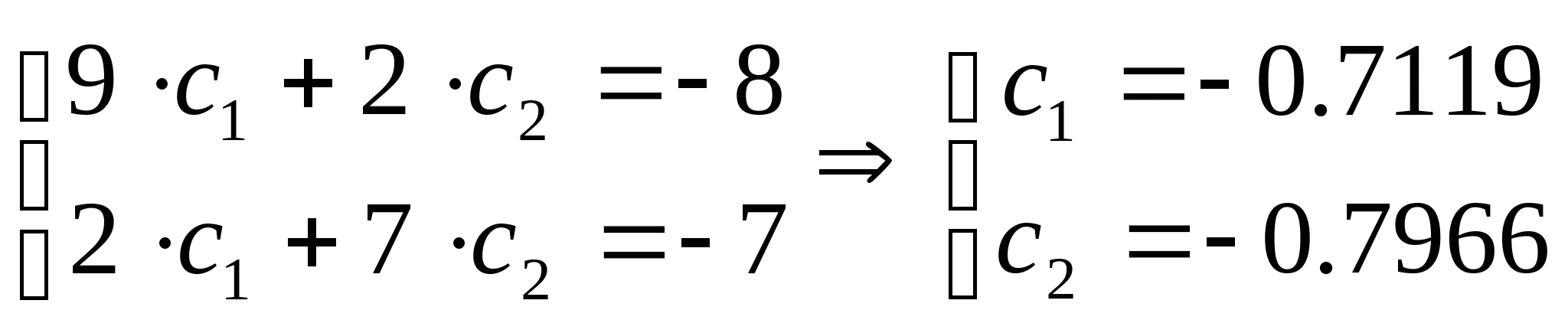
Тогда
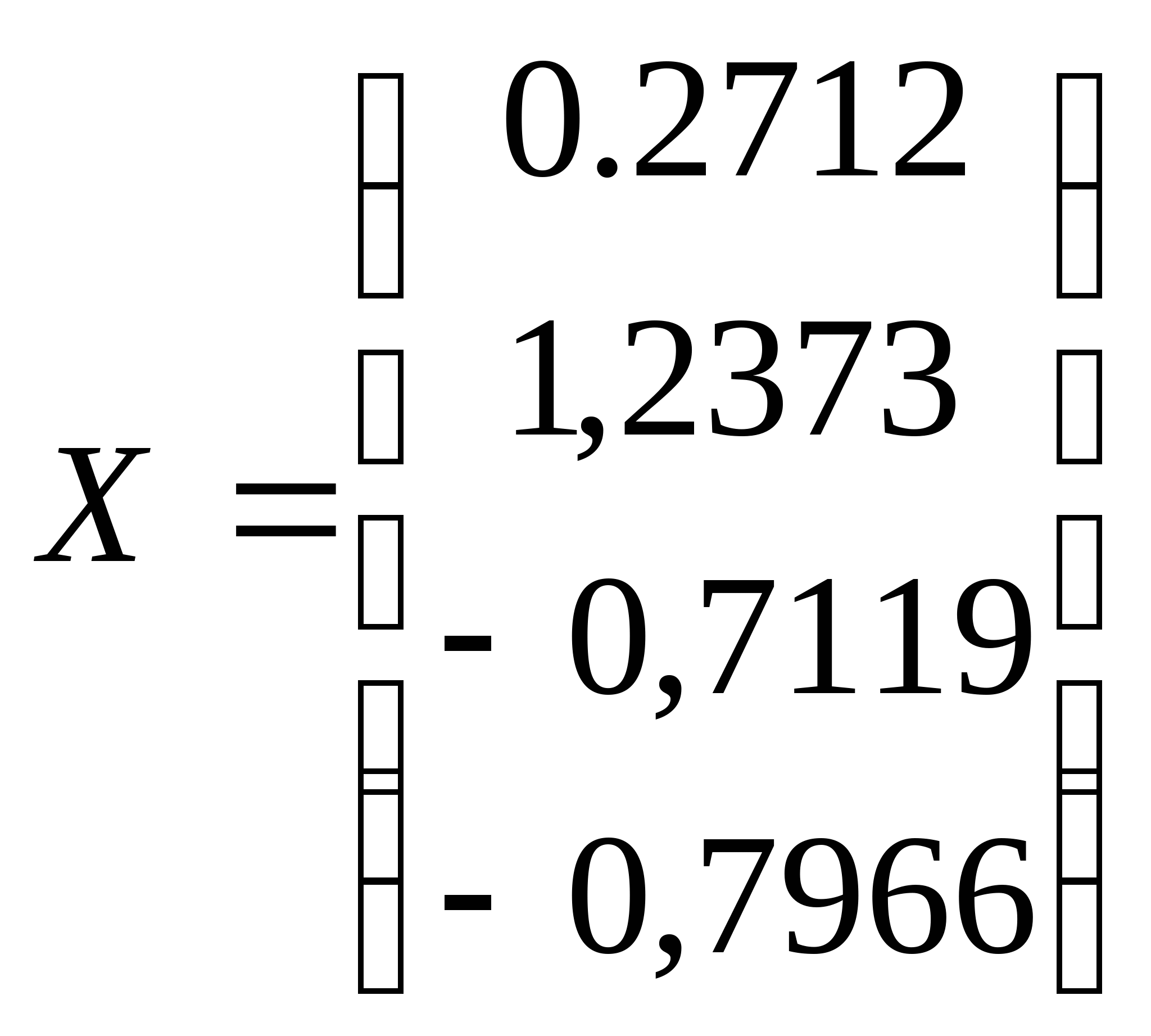 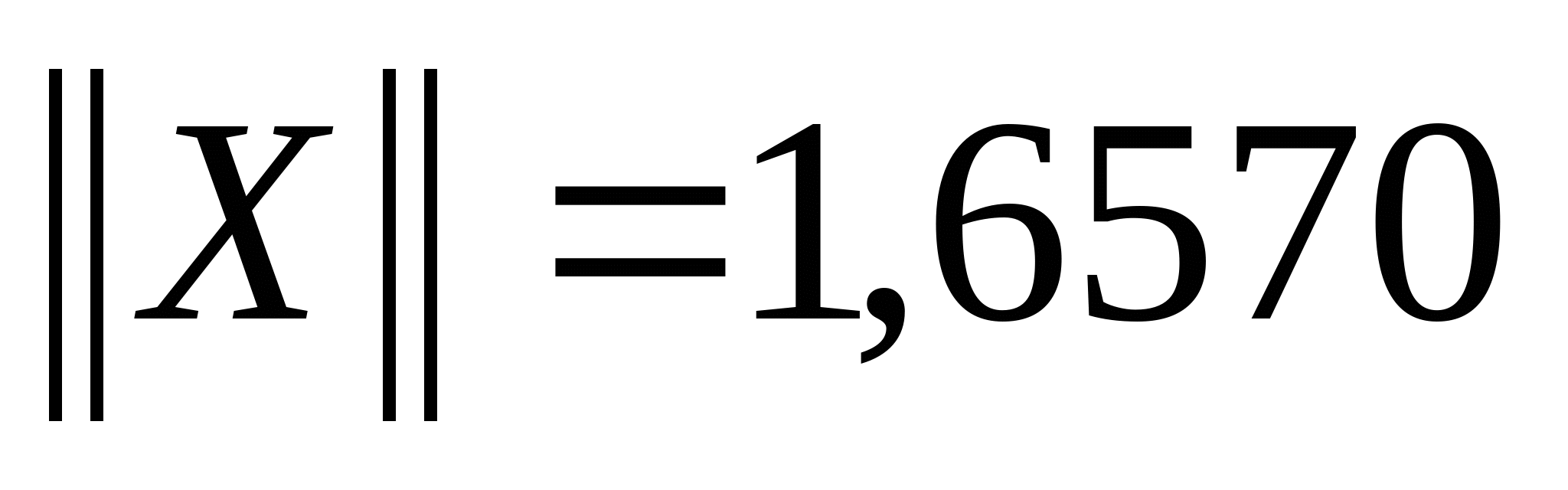 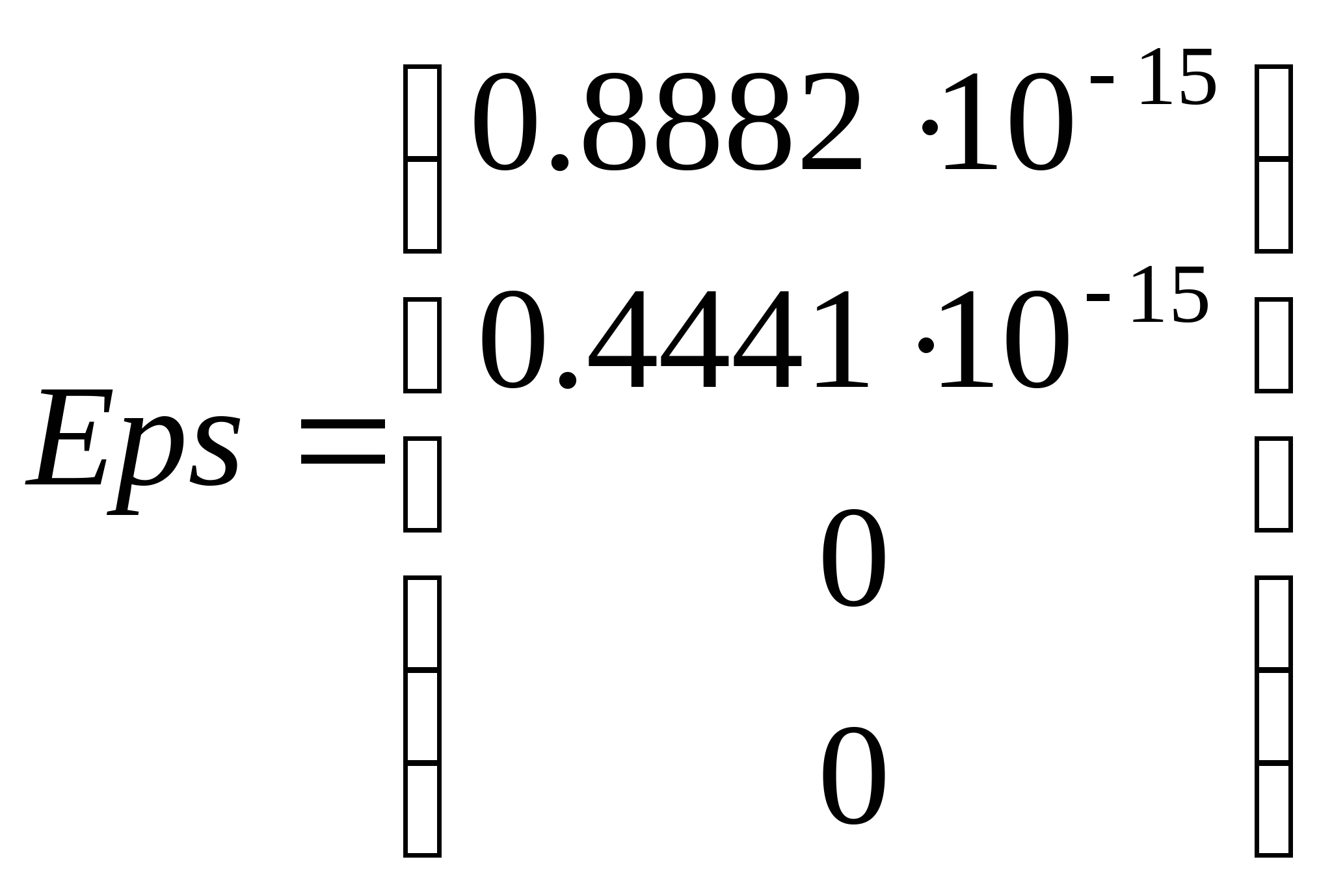
» A =
1 -3 6 -5 0 4 2 1 10 2 2 0 -9 1 6
B =
3 5 7
- - = = 1 = = - - Стандартное решение посредствам системы MatLab X = A\B X = 0 0 0.5427 0.0513 1.9722
Невязка Eps = 1.0e-015 *
0.8882 0 0
Евклидова норма N = 2.0462
- - = = 2 = = - - Решение MatLab c первоначальной диагонализацией по методу Гауса
X =
0 0 0.5427 0.0513 1.9722
Невязка Eps = 1.0e-015 *
0 -0.2220 0.0555
Евклидова норма N = 2.0462
- - = = 3 = = - - Решение системы функцией SLAE Вектор решения минимизированный по евклидовой норме 0.8957 -0.4673 0.1265 0.0113 1.0560
Евклидова норма вектора решений 1.4669
Невязка Eps = 1.0e-015 *
0.4441 0 0
% SLAE % The decision of System of the linear algebraic equations % Решение системы линейных уравнений с минимизацией % вектора решения по евклидовой норме. % % Входные параметры: % A - матрица коэффициентов системы % B - вектор столбец решения системы % Выходные параметры: % X - вектор решений (A * X = B), минимизированный по норме % N - Евклидова норма % Eps - невязка B - A*X
function [X, N] = SLAE(A, B)
if (nargin < 2) error('Необходимо ввести матрицу системы и вектор свободных коэффициентов'); end;
%Если матрица коэффициентов системы нулевая, %то вывод сообщения об ошибки и выход if (A == 0) error('Неправильное задание параметров'); end
% m - число строк, n - число столбцов [m, n] = size(A);
%Проверка на совместность системы if rank(A) ~= rank([A, B]) disp('Система не совместна'); for i = 1 : n X(i) = NaN; end X = X'; N = 0; return end
% Если высота матрицы а и столбца b не совпадают % то выдача диагностирующего сообщения if m ~= length(B) error('Высота матрицы A и столбца B не совпадают'); end
% Приведение расширенной матрицы A|B к диагональному виду A = rref([A, B]); B = A(:, n + 1); A = A(:, 1 : n); %m - число базисных строк m = rank(A); %Расчет коэффициентов С(1)..С(n-m), при которых вектор решения Х %будет минимальным по евклидовой норме. Приравнивая частные производные %нулю, составляем матрицу коэффициентов в и матрицу свободных коэффициентов E. %Соответствующие формулы смотрите в описании к программе. % i - номер строки, j - номер элемента в строке (номер столбца) for i=1:(n-m) for j=1:(n-m) D(i,j) = 0; for k=1:m D(i,j)=D(i,j)+A(k,i+m)*A(k,j+m); end if i==j D(i,j)=D(i,j)+1; end end E(i)=0; for k=1:m E(i)=E(i)+B(k)*A(k,i+m); end end
%Транспонирование вектора-строки E в вектор-столбец и %вычисление коэффициентов С(1)..С(n-m) E = E'; C = в \ E;
%Вычисление вектора решений в соответствии с найденными коэффициентами for k = m+1 : n X(k) = C(k-m); end for k = 1 : m X(k) = B(k); for j = 1 : (n - m) X(k) = X(k) - A(k, j+m)*X(j+m); end end
%Транспонирование вектора-строки X в вектор-столбец X = X';
%Вывод РЕЗУЛЬТАТОВ disp('Вектор решения минимизированный по евклидовой норме'); disp(X); N = norm(X, 'fro'); disp('Евклидова норма вектора решений'); disp(N); %disp('Невязка Eps ='); %Eps = B - A*X
return
%Тестирование функции решения систем линейных алгебраических уравнений SLAE
%Пример 1
% Матрица коэффициентов при неизвестных A = [ 1 -3 6 -5 0; 4 2 1 10 2; 2 0 -9 1 6 ] % Матрица свободных членов B = [ 3; 5; 7 ]
% --== 1 ==-- disp('- - = = 1 = = - -'); disp('Стандартное решение посредствам системы MatLab X = A\B'); X = A\B; disp('X = '); disp(X); disp('Невязка Eps = ') disp(B - A*X); disp('Евклидова норма N = ') disp(norm(X, 'fro'));
% --== 2==-- disp('- - = = 2 = = - -'); disp('Решение MatLab c первоначальной диагонализацией по методу Гауса'); % Приведение расширенной матрицы A|B к диагональному виду [m, n] = size(A); A = rref([A, B]); B = A(:, n + 1); A = A(:, 1 : n);
X = A\B disp('Невязка Eps = '); disp(B - A*X); disp('Евклидова норма N = '); disp(norm(X, 'fro'));
% --== 3 ==-- disp('- - = = 3 = = - -'); disp('Решение системы функцией SLAE'); % Повторный ввод параметров A = [ 1 -3 6 -5 0; 4 2 1 10 2; 2 0 -9 1 6 ]; B = [ 3; 5; 7 ];
[X, N3] = SLAE(A, B); disp('Невязка Eps = '); disp(B - A*X); |