   пределить графически корни уравнения: пределить графически корни уравнения:
3


. Определить графически корни уравнения: 4


. Определить графически корни уравнения:
2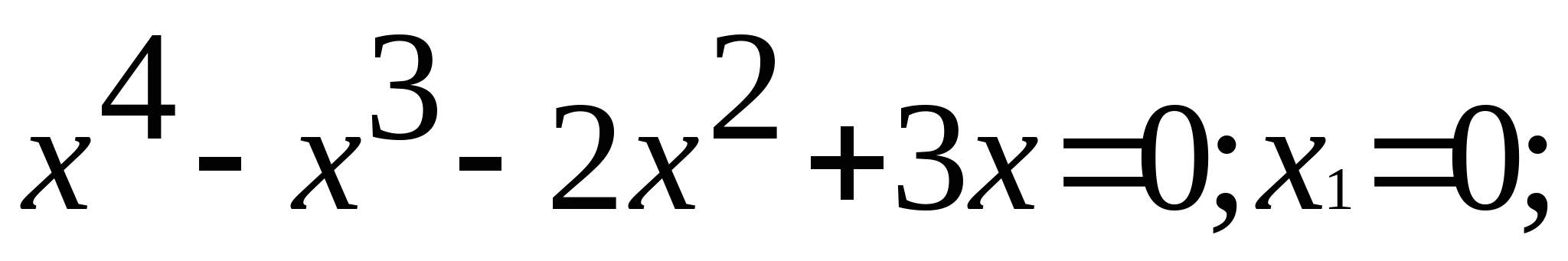 . Определить аналитически корни уравнения: . Определить аналитически корни уравнения:  
ЛАБОРАТОРНАЯ РАБОТА №10 «Методы решения систем линейных уравнений ». Студента группы ПВ-22 Малютина Максима.
Задание. Решить систему уравнений с точностью до 0,001. а) Методом итераций 
Система :

б) Методом Ньютона. С истема : истема :
uses crt; type fun=function(x:real):real; funcs=array[1..4] of fun; fun2=function(x,y:real):real;
function fun_x(y:real):real; begin fun_x:=-0.4-sin(y); end;
function fun_y(x:real):real; begin fun_y:=(cos(x+1))/2; end;
function f(x,y:real):real; begin f:=sin(x+y)-1.5*x-0.1 end;
function g(x,y:real):real; begin g:=x*x+y*y-1 end;
function dfx(x,y:real):real; begin dfx:=sin(x+y)-1.5 end;
function dfy(x,y:real):real; begin dfy:=sin(x+y) end;
function dgx(x,y:real):real; begin dgx:=2*x end;
function dgy(x,y:real):real; begin; dgy:=2*y end;
Procedure Iteration(funx,funy:fun;x,y,e,q:real); var xn,yn:real; m:byte; begin e:=abs(e*(1-q)/q); xn:=x; yn:=y; m:=0; repeat x:=xn;y:=yn; xn:=funx(y); yn:=funy(x); inc(m) until (abs(xn)+abs(yn)-abs(x)-abs(y))<e; writeln('Решение : X = ',xn,'. Y= ',yn) end;
Procedure Nuton(dfx,dfy,dgx,dgy,f,g:fun2;x,y,eps:real); var d,d1,d2,xn,yn,dx1,dy1:real; begin xn:=x;yn:=y; repeat x:=xn;y:=yn; d:=dfx(x,y)*dgy(x,y)-dfy(x,y)*dgx(x,y); d1:=-f(x,y)*dgy(x,y)+g(x,y)*dfy(x,y); d2:=-g(x,y)*dfx(x,y)+f(x,y)*dgx(x,y); dx1:=d1/d;dy1:=d2/d; xn:=x+dx1; yn:=y+dy1; until (abs(xn)+abs(yn)-abs(x)-abs(y))<eps; writeln('Решение : X = ',xn,' Y= ',yn) end;
var x,y,q,eps:real; begin clrscr; writeln('Введите заданную точность'); readln(eps); writeln('Введите начальные значения X, Y '); readln(x,y); writeln('Введите q '); readln(q); Iteration(fun_x,fun_y,x,y,eps,q); writeln('Введите начальные значения X, Y '); readln(x,y); Nuton(dfx,dfy,dgx,dgy,f,g,x,y,eps) end.
Результаты работы программы:
Введите заданную точность 0.001 Введите начальные значения X, Y -0.88 0.45 Введите q 0.9 Решение : X = -8.76048170584909E-0001. Y= 4.96164420593686E-0001 Количество шагов = 7 Введите начальные значения X, Y 0.58 0.8 Решение : X = 5.89956109385639E-0001 Y= 8.07435397634436E-0001 Количество шагов = 4 

ЛАБОРАТОРНАЯ РАБОТА №12 «Численное интегрирование ». Студента группы ПВ-22 Малютина Максима.
Задание. Различными способами вычислить приближенно значение определенного интеграла. Известно, что определенный интеграл функции  типа типа  численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y= численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y= (Рис. 1). Есть два метода вычисления этой площади или определенного интеграла — метод трапеций (Рис. 2) и метод средних прямоугольников (Рис. 3). (Рис. 1). Есть два метода вычисления этой площади или определенного интеграла — метод трапеций (Рис. 2) и метод средних прямоугольников (Рис. 3). 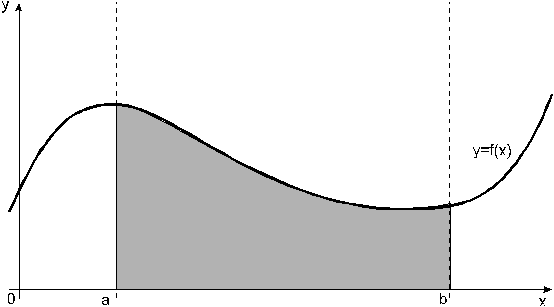 Рис. 1. Криволинейная трапеция.  Рис. 2. Метод трапеций.  Рис. 3. Метод средних прямоугольников.
По методам трапеций и средних прямоугольников соответственно интеграл равен сумме площадей прямоугольных трапеций, где основание трапеции какая-либо малая величина (точность), и сумма площадей прямоугольников, где основание прямоугольника какая-либо малая величина (точность), а высота определяется по точке пересечения верхнего основания прямоугольника, которое график функции должен пересекать в середине. Соответственно получаем формулы площадей — для метода трапеций:  , , для метода средних прямоугольников:  . . Однако существуют еще несколько методов нахождения приближенного значения определенного интеграла. Остановимся поподробнее на формуле Симпсона и т.н. формуле «трех восьмых». Формула Симпсона: 
Формула «трех восьмых»:

Число разбиений n должно быть кратно трем. Экстраполяция по Ричардсону. Пусть In1 и In2 – два приближеных значения интуграла, найденные по одной и той же формуле при n1 и n2 (n2>n1). Тогда более точное значение этого интеграла можно найти по формуле:

,где m – порядок остаточного члена (для формулы трапеций m=2, для формулы Симпсона m=4) Соответственно этим формулам и составим алгоритм. Листинг программы.
program Integral; uses Crt, Dos;
function Fx(x:real):real; begin fx:=(1+0.9*x*x)/(1.3+sqrt(0.5*x*x+1)) {В этом месте запишите функцию, для вычисления интеграла.} end;
Function Yi(x,h:real;i:LongInt):real; begin Yi:=fx(x+i*h) end;
Function CountBar(x1,x2,h:real):real; var xx1,xx2:real; c:longint; i:real; begin writeln('-->Метод средних прямоугольников.'); i:=0; for c:=1 to round(abs(x2-x1)/h) do begin write('Итерация ',c,chr(13)); xx1:=Fx(x1+c*h); xx2:=Fx(x1+c*h+h); i:=i+abs(xx1+xx2)/2*h end; writeln('------------------------------------------------'); CountBar:=i end;
Function CountTrap(x1,x2,h:real):real; var xx1,xx2,xx3:real; c:longint; i:real; begin writeln('--> Метод трапеций.'); i:=0; for c:=1 to round(abs(x2-x1)/h) do begin write('Итерация ',c,chr(13)); xx1:=Fx(x1+c*h); xx2:=Fx(x1+c*h+h); if xx2>xx1 then xx3:=xx1 else xx3:=xx2; i:=i+abs(xx2-xx1)*h+abs(xx3)*h end; writeln('------------------------------------------------'); CountTrap:=i end;
Function CountSimpson(x1,x2,h:real):real; var i:real; j,n:LongInt; begin n:=round(abs(x2-x1)/h); writeln('-->Метод Симпсона.'); i:=fx(x1); j:=2; while j<=n-1 do begin i:=i+4*yi(x1,h,j)+2*yi(x1,h,j+1); j:=j+2 end; writeln('------------------------------------------------'); CountSimpson:=h/3*(i+4*yi(x1,h,j)+yi(x1,h,j+1)); end;
Function CountThree(x1,x2,h:real):real; var s1,s2,s3:real; i,n:LongInt; begin writeln('-->Метод "Трех восьмых".'); n:=round((abs(x2-x1))/h); if n mod 3=0 then begin s1:=fx(x1)+fx(x2); s2:=0;s3:=0; for i:=1 to n do begin if i mod 3=0 then s3:=s3+yi(x1,h,i) else s2:=s2+yi(x1,h,i) end; CountThree:=3*h/8*(s1+3*s2+2*s3); writeln('------------------------------------------------') end else writeln('Неверное число шагов !!! (Должно быть кратно 3) ') end;
Function Richardson(i1,i2,m,a:real):double; var b:double; begin b:=a/(exp(m*ln(a))-1); Richardson:=i2+b*(i2-i1) end;
var i1,i2,i,x1,x2,h1,h2:real; c:byte; n1,n2,m:word; begin writeln('------------------------------------------------'); writeln('-= Программа вычисления определенного интеграла =-'); writeln('Введите исходные значения: '); write('Начальное значение x (x нижн)=');Readln(x1); write('Конечное значение x (x верхн)=');Readln(x2); repeat write('Вычисление по числу итераций(1) или по шагу(2)? ');readln(c); until (c=1) or (c=2); case c of 1: begin write('Количество итераций (n1)=');Readln(n1); write('Количество итераций (n2)=');Readln(n2); h1:=(abs(x2-x1))/n1; h2:=(abs(x2-x1))/n2; writeln('Шаг вычисления (h1)=',h1); writeln('Шаг вычисления (h2)=',h2) end; 2: begin write('Шаг вычисления (h1)=');Readln(h1); write('Шаг вычисления (h2)=');Readln(h2); writeln('Количество итераций (n1)=',round(abs(x2-x1)/h1)); writeln('Количество итераций (n2)=',round(abs(x2-x1)/h2)) end; end; i1:=CountTrap(x1,x2,h1); writeln('Интеграл=',i1); i2:=CountTrap(x1,x2,h2); writeln('Интеграл=',i2); writeln('Экстраполирование Ричардсона для случая трапеций: '); writeln('Интеграл = ',Richardson(i1,i2,2,n2/n1)); readln; i1:=CountBar(x1,x2,h1); writeln('Интеграл = ',i1); i2:=CountBar(x1,x2,h2); writeln('Интеграл = ',i2); writeln('Экстраполирование Ричардсона для случая прямоугольников '); writeln('Интеграл = ',Richardson(i1,i2,3,n2/n1)); writeln('------------------------------------------------'); i1:=CountSimpson(x1,x2,h1); writeln('Интеграл = ',i1); i2:=CountSimpson(x1,x2,h2); writeln('Интеграл = ',i2); writeln('Экстраполирование Ричардсона для случая Симпсона '); writeln('Интеграл = ',Richardson(i1,i2,3,n2/n1)); i1:=CountThree(x1,x2,h1); writeln('Интеграл = ',i1); i2:=CountThree(x1,x2,h2); writeln('Интеграл = ',i2); writeln('Спасибо за использование программы ;-) '); readln end.
Результаты работы программы:
------------------------------------------------ -= Программа вычисления определенного интеграла =- Введите исходные значения: Начальное значение x (x нижн)=0.9 Конечное значение x (x верхн)=2.34 Вычисление по числу итераций(1) или по шагу(2)? 1 Количество итераций (n1)=4 Количество итераций (n2)=5 Шаг вычисления (h1)= 3.60000000000127E-0001 Шаг вычисления (h2)= 2.88000000000011E-0001 --> Метод трапеций. ------------------------------------------------ Интеграл= 3.21492525852918E-0003 --> Метод трапеций. ------------------------------------------------ Интеграл= 4.61840165326066E-0003 Экстраполирование Ричардсона для случая трапеций: Интеграл = 7.73723808599729E-0003 ------------------------------------------------ Интеграл = 2.53128978246764E-0003 Экстраполирование Ричардсона для случая прямоугольников Интеграл = 3.65111028007424E-0003 ------------------------------------------------ -->Метод Симпсона. ------------------------------------------------ Интеграл = 1.07491181758519E-0002 -->Метод Симпсона. ------------------------------------------------ Интеграл = 9.02681082661161E-0003 Экстраполирование Ричардсона для случая Симпсона Интеграл = 6.76804708990304E-0003 ------------------------------------------------ -->Метод "Трех восьмых". Неверное число шагов !!! (Должно быть кратно 3) Интеграл = 0.00000000000000E+0000 ------------------------------------------------ -->Метод "Трех восьмых". Неверное число шагов !!! (Должно быть кратно 3) Интеграл = 0.00000000000000E+0000 ------------------------------------------------ -->Метод Гаусса. Интеграл = 1.40977850823276E-0002 ------------------------------------------------ -->Метод Гаусса. Интеграл = 1.40649829885291E-0002 Спасибо за использование программы ;-)
З адание 1. Отделить корни уравнения графически и уточнить один из них методом хорд с точностью до 0,001. адание 1. Отделить корни уравнения графически и уточнить один из них методом хорд с точностью до 0,001. 
x =0.672275594. Количество шагов – 5. =0.672275594. Количество шагов – 5.
З адание 2. Отделить корни уравнения аналитически и уточнить один из них методом хорд с точностью до 0,001. адание 2. Отделить корни уравнения аналитически и уточнить один из них методом хорд с точностью до 0,001.


x=-0.3219021. Количество шагов – 5.
То же самое методом хорд: 1. x=0.67235827. Количество шагов – 3. 2. x=-0.3222222. Количество шагов – 3.
З адание 1. Комбинированным методом хорд и касательных решить уравнение 3-ей степени, вычислив корни с точностью до 0,001. адание 1. Комбинированным методом хорд и касательных решить уравнение 3-ей степени, вычислив корни с точностью до 0,001. 


X1=-0.810246. Количество шагов – 2. X2= 1.168039. Количество шагов – 2. X3=2.641798. Количество шагов – 2. {определение корня методом хорд} uses crt;
function fun(x:real):real;{заданная функция} Begin fun:=x+ln(x)/ln(10)-0.5; End;
function fun2(x:real):real;{вторая производная заданной функции} Begin fun2:=-1/ln(10)/x/x; End;
var a,b,e,e1,min,max,x,x1,n,f,f1:real; m:byte; BEGIN clrscr; writeln('Введите промежуток где возможен корень'); write('a=');readln(a); write('b=');readln(b); write('Введите точность E=');readln(e); writeln('Введите m и M'); write('m=');readln(min); write('M=');readln(max); if fun(a)*fun2(a)>0 then begin n:=a; x:=b; end else begin n:=b; x:=a; end; f:=fun(n); e1:=(e*min)/(max-min); m:=0; repeat x1:=x; f1:=fun(x1); x:=x1-(f1*(n-x1))/(f-f1); m:=m+1; until e1>=abs(x-x1); writeln('Корень =',x); writeln(m); END.
{определение корня методом Ньютона} uses crt; function fun(x:real):real;{заданная функция} Begin fun:=x*x*x+3*x+1; End;
function fun1(x:real):real;{первая производная} Begin fun1:=3*(x*x+1); End;
function fun2(x:real):real;{вторая производная} Begin fun2:=6*x; End;
var a,b,e,e1,min,max,x,x1,n:real; m:byte;
BEGIN clrscr; writeln('Введите промежуток где возможен корень'); write('a=');readln(a); write('b=');readln(b); write('Введите точность E=');readln(e); writeln('Введите m и M'); write('m=');readln(min); write('M=');readln(max); if fun(a)*fun2(a)>0 then begin n:=b; x:=a; end else begin n:=a; x:=b; end; e1:=sqrt((2*min*e)/max); m:=0; repeat x1:=x; x:=x1-fun(x1)/fun1(x1); m:=m+1; until e1>=abs(x-x1); writeln('Корень =',x); writeln(m); END. {определение корня комбинированным методом} uses crt; function fun(x:real):real;{заданная функция} Begin fun:=x*x*x-3*x*x+2.5; End; function fun1(x:real):real;{первая производная} Begin fun1:=3*x*(x-2); End; function fun2(x:real):real;{вторая производная} Begin fun2:=6*x-6; End; procedure chord(n,x1:real;var x:real);{метод хорд} Begin x:=x1-(fun(x1)*(n-x1))/(fun(n)-fun(x1)); End; procedure nuton(x1:real;var x:real);{метод Ньютона} Begin x:=x1-fun(x1)/fun1(x1); End; var x,a,b,e,xx,x1,xn,n,n1:real; m:byte; BEGIN clrscr; writeln('Введите промежуток где возможен корень'); write('a=');readln(a); write('b=');readln(b); write('Введите точность E=');readln(e); if fun(a)*fun2(a)>0 then begin n:=a;x:=b; n1:=b;x1:=a; end else begin n:=b;x:=a; n1:=a;x1:=b; end; m:=0; repeat nuton(x1,xn); chord(xn,x,xx); x:=xx; x1:=xn; m:=m+1; until abs(xx-xn)<=e; writeln('Корень =',(xx+xn)/2); writeln(m); END.
Задание 1. Отделить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001. 


X=0,213310688. Количество шагов – 3.
З 

адание 2. Отделить корни уравнения аналитически и уточнить один из них методом итераций с точностью до 0,001.
X=-1,1246907. Количество шагов – 4.
{определение корня методом итераций} uses crt; function fun(x:real):real; begin fun:=x*x*x-0.1*x*x+0.4*x+2; end;
function fun1(x:real):real; begin fun1:=3*x*x-0.2*x+0.4; end;
var u,x,xn,q:real; min,max:real; a,b,e:real; m:byte; begin clrscr; writeln('Введите промежуток где возможен корень'); write('a=');readln(a); write('b=');readln(b); write('Введите точность E=');readln(e); writeln('Введите m и M'); write('m=');readln(min); write('M=');readln(max); u:=2/(min+max); q:=(max-min)/(max+min); e:=abs(e*(1-q)/q); x:=a; m:=0; repeat xn:=x; x:=xn-u*fun(xn); m:=m+1; until abs(x-xn)<e; writeln('Корень =',x); writeln(m); end.
ЛАБОРАТОРНАЯ РАБОТА №3 «Алгебра матриц». Студента группы ПВ-22 Малютина Максима.
Задание. Обратить матрицу методом разбиения ее на произведение двух треугольных матриц.
В ариант 8. ариант 8.
При разбиении матрицы А на две треугольные, используются следующие формулы: 
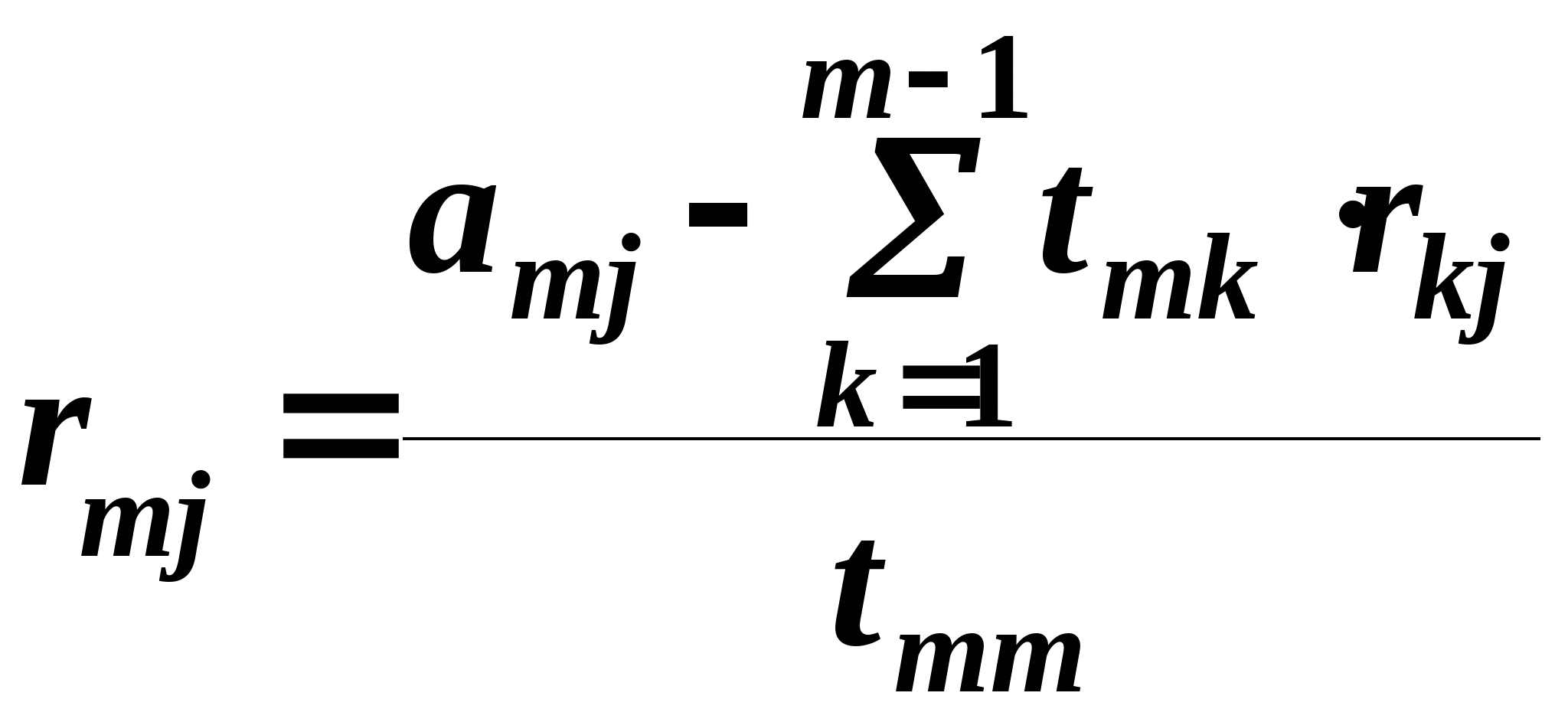
M =1..n. =1..n.
Получены следующие результаты: М  атрица T: Матрица R: атрица T: Матрица R:

Матрица A-1:
program lab_3; { Лабораторная работа по вычмслительной математике N 3 Нахождение матрицы, обратной данной }
const Sizem = 10; { максимальная размерность матрицы }
type mattype = array [1..Sizem,1..Sizem] of double;
{ процедура для вывода матрицы на экран } procedure WriteMat (var m : mattype;n,n1 : byte); var k,i : byte; begin writeln; for k := 1 to n do begin for i := 1 to n1 do write(m[k,i] : 7:3,' '); writeln end; end;
{ процедура ввода значений элементов матрицы } procedure inputmat (var m : mattype; var n : byte); var k,i : byte; begin writeln; write ('Размер матрицы = '); readln(n); for k := 1 to n do for i := 1 to n do read (m[k,i]); end;
{ процедура транспонирования матрицы } procedure Transpose (var m : mattype;n : byte); var k,i : byte; ttt : double; begin for k := 1 to n do for i := k+1 to n do begin ttt := m[k,i]; m[k,i] := m[i,k]; m[i,k] := ttt; end; end;
{ процедура умножения двух матриц (a*b=c) } procedure MulMat (a : mattype; ma,na : byte; b : mattype; mb,nb : byte; var c : mattype; var mc,nc : byte); var k,i,j : byte; s : double; begin if na = nb then begin mc := ma; nc := nb; for k := 1 to mc do for j := 1 to nc do begin s := 0; for i := 1 to nc do s := s+a[k,i]*b[i,j]; c[k,j] := s; end; end else begin writeln('Неправильный размер матрицы !'); halt end; end;
{ процедура получения двух треугольных матриц произведение которых равно матрице m } procedure GetRnT (var m,r,t : mattype; n : byte); var k,i,m1,l : byte; begin for k := 1 to n do for i := 1 to n do begin if k=i then r[k,i] := 1 else r[k,i] := 0; t[k,i] := 0; end;
for m1 := 1 to n do begin if m1 = 1 then begin for i := 1 to n do t[i,1] := m[i,1]; for i := 2 to n do r[1,i] := m[1,i]/t[1,1]; end else begin k := m1; for i := m1 to n do begin t[i,k] := m[i,k]; for l := 1 to k-1 do t[i,k] := t[i,k] - t[i,l]*r[l,k]; end; i := m1; for k := i+1 to n do begin r[i,k] := m[i,k]; for l := 1 to i-1 do r[i,k] := r[i,k] - t[i,l]*r[l,k]; r[i,k] := r[i,k] / t[i,i]; end; end; end; end;
{ процедура обращения нижней треугольной матрицы } procedure BackMat (var t : mattype; n : byte); var i,k,l : byte; x : mattype; begin for i := 1 to n do x[i,i] := 1/t[i,i];
for k := 1 to n-1 do for i := k+1 to n do begin x[i,k] := 0; for l := k to i-1 do x[i,k] := x[i,k] - t[i,l]*x[l,k]; x[i,k] := x[i,k]/t[i,i]; end; t := x end;
var m,m1,r,t : mattype; n : byte; { ------------- основная программа ---------------- } begin writeln ('Лабораторная работа N 2 '); InputMat(m,n); { ввод матрицы m } GetRnT(m,r,t,n);{получение треугольных матриц t и r} Writeln('Матрица T: '); WriteMat(t,n,n); readln; Writeln('Матрица R: '); WriteMat(r,n,n); readln; BackMat(t,n); { обращение матрицы t } Transpose(r,n); { транспонирование матрицы r } BackMat(r,n); {обращение матрицы r (транcпонир.)} Transpose(r,n);{транспонирование обращенной м-цы r } MulMat(r,n,n,t,n,n,m1,n,n); {получение матрицы,обратной матрице m} WriteMat (m1,n,n);{ печать обратной матрицы } readln; MulMat(m,n,n,m1,n,n,m,n,n); { Проверка вычислений } WriteMat(m,n,n); readln; end.
ЛАБОРАТОРНАЯ РАБОТА №4 «Методы решения систем линейных уравнений ». Студента группы ПВ-22 Малютина Максима.
Задание. Решить систему по схеме Халецкого с точностью до 0,0001.
В ариант 8. ариант 8.
При разбиении матрицы А на две треугольные, используются следующие формулы: 

M =1..n. =1..n.
 
Получены следующие результаты: М  атрица T: Матрица R: атрица T: Матрица R:

Матрица X:
program lab_3; { Лабораторная работа по вычмслительной математике N 3 Нахождение матрицы, обратной данной }
const Sizem = 10; { максимальная размерность матрицы }
type mattype = array [1..Sizem,1..Sizem] of double;
{ процедура для вывода матрицы на экран } procedure WriteMat (var m : mattype;n,n1 : byte); var k,i : byte; begin writeln; for k := 1 to n do begin for i := 1 to n1 do write(m[k,i] : 7:3,' '); writeln end; end;
{ процедура ввода значений элементов матрицы } procedure inputmat (var m : mattype; var n : byte); var k,i : byte; begin writeln; write ('Размер матрицы = '); readln(n); for k := 1 to n do for i := 1 to n do read (m[k,i]); end;
{ процедура транспонирования матрицы } procedure Transpose (var m : mattype;n : byte); var k,i : byte; ttt : double; begin for k := 1 to n do for i := k+1 to n do begin ttt := m[k,i]; m[k,i] := m[i,k]; m[i,k] := ttt; end; end;
{ процедура умножения двух матриц (a*b=c) } procedure MulMat (a : mattype; ma,na : byte; b : mattype; mb,nb : byte; var c : mattype; var mc,nc : byte); var k,i,j : byte; s : double; begin if na = nb then begin mc := ma; nc := nb; for k := 1 to mc do for j := 1 to nc do begin s := 0; for i := 1 to nc do s := s+a[k,i]*b[i,j]; c[k,j] := s; end; end else begin writeln('Неправильный размер матрицы !'); halt end; end;
{ процедура получения двух треугольных матриц произведение которых равно матрице m } procedure GetRnT (var m,r,t : mattype; n : byte); var k,i,m1,l : byte; begin for k := 1 to n do for i := 1 to n do begin if k=i then r[k,i] := 1 else r[k,i] := 0; t[k,i] := 0; end;
for m1 := 1 to n do begin if m1 = 1 then begin for i := 1 to n do t[i,1] := m[i,1]; for i := 2 to n do r[1,i] := m[1,i]/t[1,1]; end else begin k := m1; for i := m1 to n do begin t[i,k] := m[i,k]; for l := 1 to k-1 do t[i,k] := t[i,k] - t[i,l]*r[l,k]; end; i := m1; for k := i+1 to n do begin r[i,k] := m[i,k]; for l := 1 to i-1 do r[i,k] := r[i,k] - t[i,l]*r[l,k]; r[i,k] := r[i,k] / t[i,i]; end; end; end; end;
{ процедура обращения нижней треугольной матрицы } procedure BackMat (var t : mattype; n : byte); var i,k,l : byte; x : mattype; begin for i := 1 to n do x[i,i] := 1/t[i,i];
for k := 1 to n-1 do for i := k+1 to n do begin x[i,k] := 0; for l := k to i-1 do x[i,k] := x[i,k] - t[i,l]*x[l,k]; x[i,k] := x[i,k]/t[i,i]; end; t := x end;
var m,m1,r,t : mattype; n : byte; { ------------- основная программа ---------------- } begin writeln ('Лабораторная работа N 2 '); InputMat(m,n); { ввод матрицы m } GetRnT(m,r,t,n);{получение треугольных матриц t и r} Writeln('Матрица T: '); WriteMat(t,n,n); readln; Writeln('Матрица R: '); WriteMat(r,n,n); readln; BackMat(t,n); { обращение матрицы t } Transpose(r,n); { транспонирование матрицы r } BackMat(r,n); {обращение матрицы r (транcпонир.)} Transpose(r,n);{транспонирование обращенной м-цы r } MulMat(r,n,n,t,n,n,m1,n,n); {получение матрицы,обратной матрице m} WriteMat (m1,n,n);{ печать обратной матрицы } readln; MulMat(m,n,n,m1,n,n,m,n,n); { Проверка вычислений } WriteMat(m,n,n); readln; end.
ЛАБОРАТОРНАЯ РАБОТА №5 «Методы решения систем линейных уравнений ». Студента группы ПВ-22 Малютина Максима.
Задание. Решить систему линейных уравнений методом квадратных корней с точностью до 0,001.
В ариант 8. ариант 8.
При разбиении матрицы А на треугольную используются следующая формулы: 
j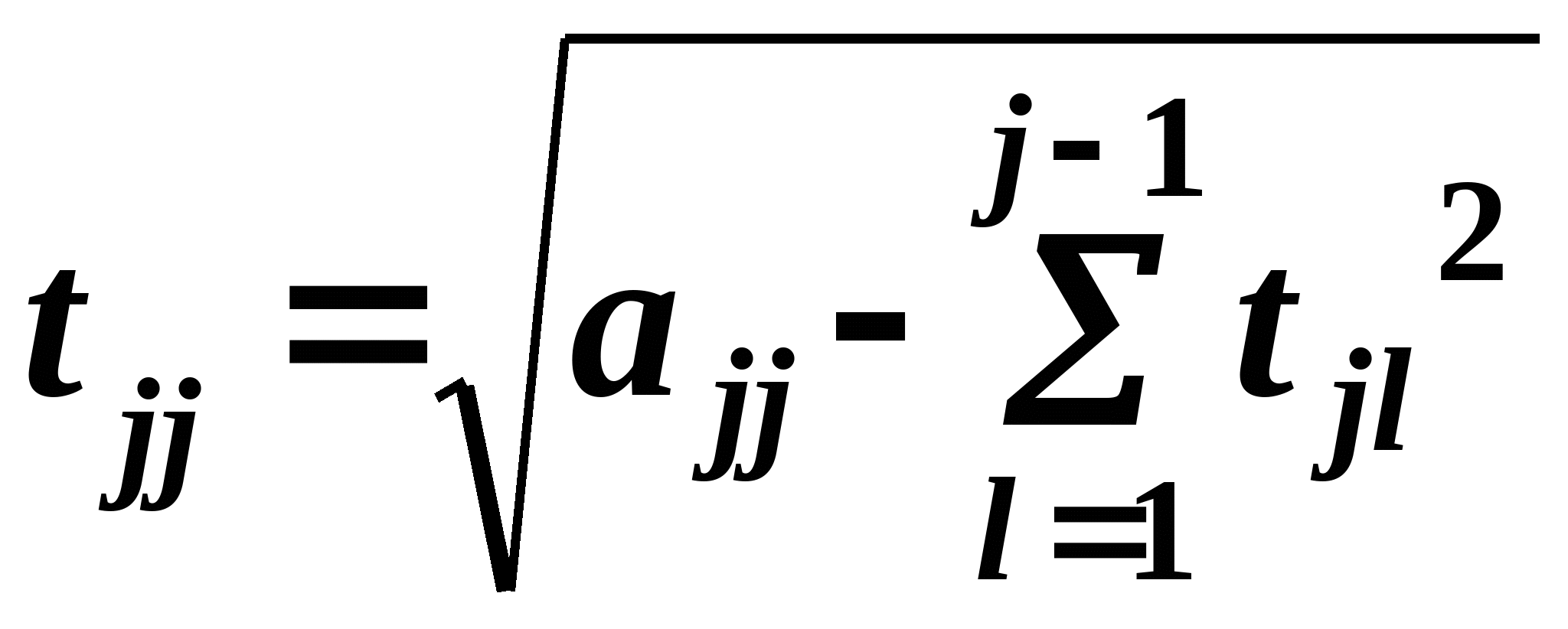 =1..n. =1..n.



const size=10; type vector=array[1..size] of real; matrix=array[1..size] of vector;
Procedure InputVector(var a:vector;n:byte); var i:byte; begin for i:=1 to n do begin writeln('Введите ',i,'-ый элемент '); readln(a[i]); end; end;
Procedure InputMatrix(var a:matrix;n:byte); var i:byte; begin for i:=1 to n do begin writeln('Введите ',i,'-ую строку матрицы '); InputVector(a[i],n) end; end;
Procedure OutputVector(var a:vector;n:byte); var i:byte; begin for i:=1 to n do write(a[i]:10:5); writeln end;
Procedure OutputMatrix(var a:matrix;n:byte); var i:byte; begin for i:=1 to n do outputvector(a[i],n) end;
Procedure GetT(var t:matrix;a:matrix;n:byte); var i,j,l:byte; s:real; begin for i:=1 to n do for j:=1 to n do t[i,j]:=0; for j:=1 to n do begin s:=0; for l:=1 to j-1 do s:=s+sqr(t[j,l]); s:=a[j,j]-s; t[j,j]:=sqrt(s); for i:=j+1 to n do begin s:=0; for l:=1 to j-1 do s:=s+t[i,l]*t[j,l]; t[i,j]:=(a[i,j]-s)/t[j,j] end; end; end;
procedure MulMatrix(a:matrix;ma,na:byte;b:matrix;mb,nb:byte;var c:matrix;var mc,nc:byte); var i,j,k:byte; s:real; begin if na=nb then begin mc:=ma; nc:=nb; for k:=1 to mc do for j:=1 to nc do begin s:=0; for i:=1 to nc do s:=s+a[k,i]*b[i,j]; c[k,j]:=s end; end else begin writeln('Неверные размеры матриц !!! '); halt end; end;
procedure MulVector(a:matrix;ma,na:byte;b:vector;nb:byte;var c:vector;var nc:byte); var i,j:byte; s:real; begin if na=nb then begin nc:=nb; for i:=1 to nc do begin s:=0; for j:=1 to nc do s:=s+a[i,j]*b[j]; c[i]:=s; end; end else begin writeln('Неверные размеры матриц !!! '); halt end; end;
Procedure TransposeMatrix(var a:matrix;n:byte); var i,j:byte; s:real; begin for i:=1 to n do for j:=1 to n do begin s:=a[i,j]; a[i,j]:=a[j,i]; a[j,i]:=s end; end;
procedure GetY(t:matrix;b:vector;var y:vector;n:byte); var i,k:byte; s:real; begin for i:=1 to n do begin s:=0; for k:=1 to i-1 do s:=s+t[i,k]*y[k]; y[i]:=(b[i]-s)/t[i,i]; end; end;
procedure GetX(t:matrix;y:vector;var x:vector;n:byte); var j,k:byte; s:real; begin for j:=n downto 1 do begin s:=0; for k:=j+1 to n do s:=s+t[k,j]*x[k]; x[j]:=(y[j]-s)/t[j,j]; end; end;
var a,at,at2,t:matrix; b,b2,y,x:vector; n:byte; begin writeln('Введите размерность матрицы коэффициентов ');readln(n); writeln('Введите элементы матрицы коэффициентов '); InputMatrix(a,n); writeln('Введите вектор свободных членов '); InputVector(b,n); at:=a; TransposeMatrix(at,n); MulMatrix(a,n,n,at,n,n,at2,n,n); MulVector(at,n,n,b,n,b2,n); Writeln('Пребразованная матрица А: '); at:=at2; outputmatrix(at,n); Writeln('Преобразованный вектор B: '); b:=b2; outputvector(b,n); writeln; GetT(t,at,n); Writeln('Пребразованная матрица T: '); outputmatrix(t,n); GetY(t,b,y,n); writeln('Вектор Y'); outputvector(y,n); GetX(t,y,x,n); writeln('Вектор X'); outputvector(x,n) end.
Пребразованная матрица А:Преобразованный вектор B: 4.97540 1.82880 1.26010 -0.14480 4.23870 -4.67000 1.82880 3.64830 -1.77800 1.26010 -1.77800 3.78260
Пребразованная матрицаT:Вектор Y 2.23056 0.00000 0.00000 -0.06492 2.48788 -1.05155 0.81988 1.72514 0.00000 Вектор X 0.56493 -1.29913 1.33256 -0.14090 0.84788 -0.78912
ЛАБОРАТОРНАЯ РАБОТА №6 «Методы решения систем линейных уравнений ». Студента группы ПВ-22 Малютина Максима.
Задание. Решить систему линейных уравнений методом Гаусса с выбором максимального элемента по столбцу с точностью до 0,001.
В ариант 8. ариант 8.
При решении системы уравнений методом Гаусса используются следующие формулы: Шаг № I: (i:=1, n-1) Среди элементов i столбца (начиная с i-ой строки до n-ой) выбираем max по модулю элемент. Если их несколько, выбираем первый. Меняем местами i-ое уравнение и отмеченное. Далее проводим i-ый шаг метода Гаусса: j:=i+1,n mj = aji / aii; Вычисляем mj Далее исключаем xi: Вычитаем из строк i+1..n i-ую строку, помноженную на m: k:=i+1,n j:=1,n akj = akj - aij * mk bk = bk – bi * mk
Д

алее осуществляется обратный ход метода Гаусса:
program gauss_max; const size=10; type vector=array[1..size] of real; matrix=array[1..size] of vector;
Procedure InputVector(var a:vector;n:byte); var i:byte; begin for i:=1 to n do begin writeln('Введите ',i,'-ый элемент '); readln(a[i]); end; end;
Procedure InputMatrix(var a:matrix;n:byte); var i:byte; begin for i:=1 to n do begin writeln('Введите ',i,'-ую строку матрицы '); InputVector(a[i],n) end; end;
Procedure OutputVector(var a:vector;n:byte); var i:byte; begin for i:=1 to n do write(a[i]:10:5); writeln end;
Procedure OutputMatrix(var a:matrix;n:byte); var i:byte; begin for i:=1 to n do outputvector(a[i],n) end;
Procedure MulVector(a:matrix;ma,na:byte;b:vector;nb:byte;var c:vector;var nc:byte); var i,j:byte; s:real; begin if na=nb then begin nc:=nb; for i:=1 to nc do begin s:=0; for j:=1 to nc do s:=s+a[i,j]*b[j]; c[i]:=s end; end else begin writeln('Неверные размеры матриц !!! '); halt end; end;
Procedure SwapVector(var a,b:vector); var n:vector; begin n:=a; a:=b; b:=n end;
Procedure Swap(var a,b:real); var n:real; begin n:=a; a:=b; b:=n end;
Procedure GetMaxEl(a:matrix;n,i:byte;var l:byte); var k:byte; max:real; begin max:=abs(a[i,i]);l:=i; for k:=i to n do if abs(a[k,i])>max then begin max:=abs(a[k,i]); l:=k end; end;
Procedure GetAm(var a:matrix;var b:vector;n:byte); var i,j,k,l:byte; m:vector; begin for i:=1 to n-1 do begin GetMaxEl(a,n,i,l); SwapVector(a[i],a[l]); Swap(b[i],b[l]); for j:=i+1 to n do m[j]:=a[j,i]/a[i,i]; for k:=i+1 to n do begin for j:=1 to n do a[k,j]:=a[k,j]-a[i,j]*m[k]; b[k]:=b[k]-b[i]*m[k] end; end; end;
Procedure GetX(a:matrix;b:vector;n:byte;var x:vector); var k,l:byte; s:real; begin x[n]:=b[n]/a[n,n]; for k:=n-1 downto 1 do begin s:=0; for l:=k+1 to n do s:=s+a[k,l]*x[l]; x[k]:=(b[k]-s)/a[k,k] end; end;
var a,am:matrix; b,x,x2:vector; n:byte; begin writeln('Введите размерность матрицы коэффициентов ');readln(n); writeln('Введите элементы матрицы коэффициентов '); InputMatrix(a,n); writeln('Введите вектор свободных членов '); InputVector(b,n); am:=a; GetAm(am,b,n); writeln('Матрица Am '); outputmatrix(am,n); GetX(am,b,n,x); writeln('Вектор X '); outputvector(x,n); MulVector(a,n,n,x,n,x2,n); writeln('Проверка: Вектор X2 - умножение матрицы Am на X '); outputvector(x2,n) end.
Матрица А:Вектор B: 10.00000 6.00000 2.00000 0.00000 25.00000 8.00000 2.50000 1.50000 0.00000 6.00000 -2.00000 2.00000 0.00000 3.20000 0.40000 -1.00000 0.00000 -2.00000 -3.00000 4.00000
Матрица Am 10.00000 6.00000 2.00000 0.00000 0.00000 6.00000 -2.00000 2.00000 0.00000 0.00000 -3.66667 4.66667 0.00000 -0.00000 -0.00000 -0.20000
Вектор X 2.00000 1.00000 -0.50000 0.50000
Проверка: Вектор X2 - умножение матрицы Am на X 25.00000 8.00000 2.50000 1.50000
ЛАБОРАТОРНАЯ РАБОТА №7 «Методы решения систем линейных уравнений ». Студента группы ПВ-22 Малютина Максима.
Задание. Составить программу, отладить ее на тестовом примере, рассмотренном на лекции.
С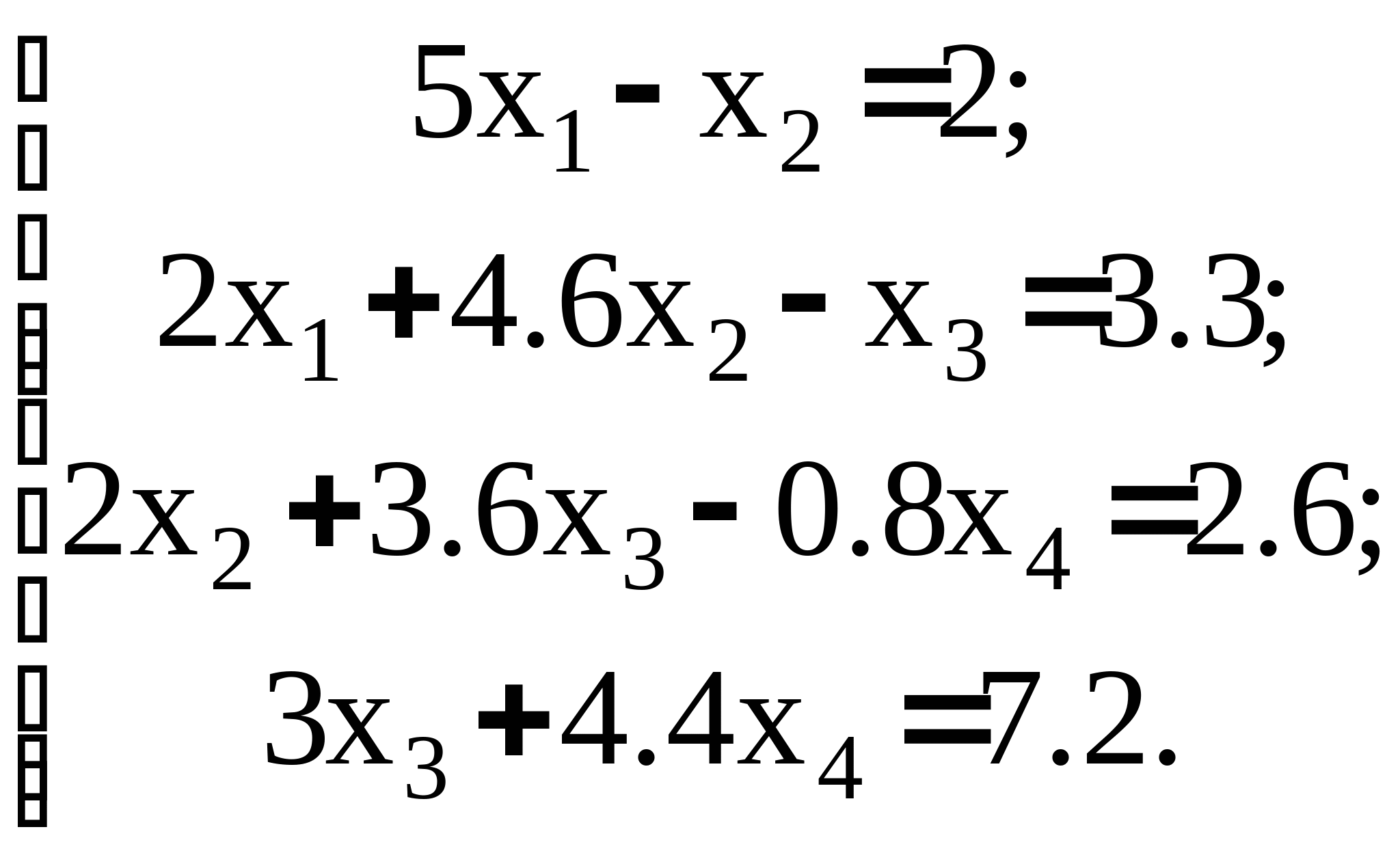 истема : истема :
При решении примера на лекции: x1 = 0.526; x2 =0.628; x3 = 0.64; x4 = 1.2.
Векторы a, b, c, d. a = {0; 2; 2; 3} b = {5; 4.6; 3.6; 4.4} c = {-1; -1; -0.8; 0} d = {2; 3.3; 2.6; 7.2}
Прямой ход прогонки заключается в нахождении прогоночных коэффициентов: 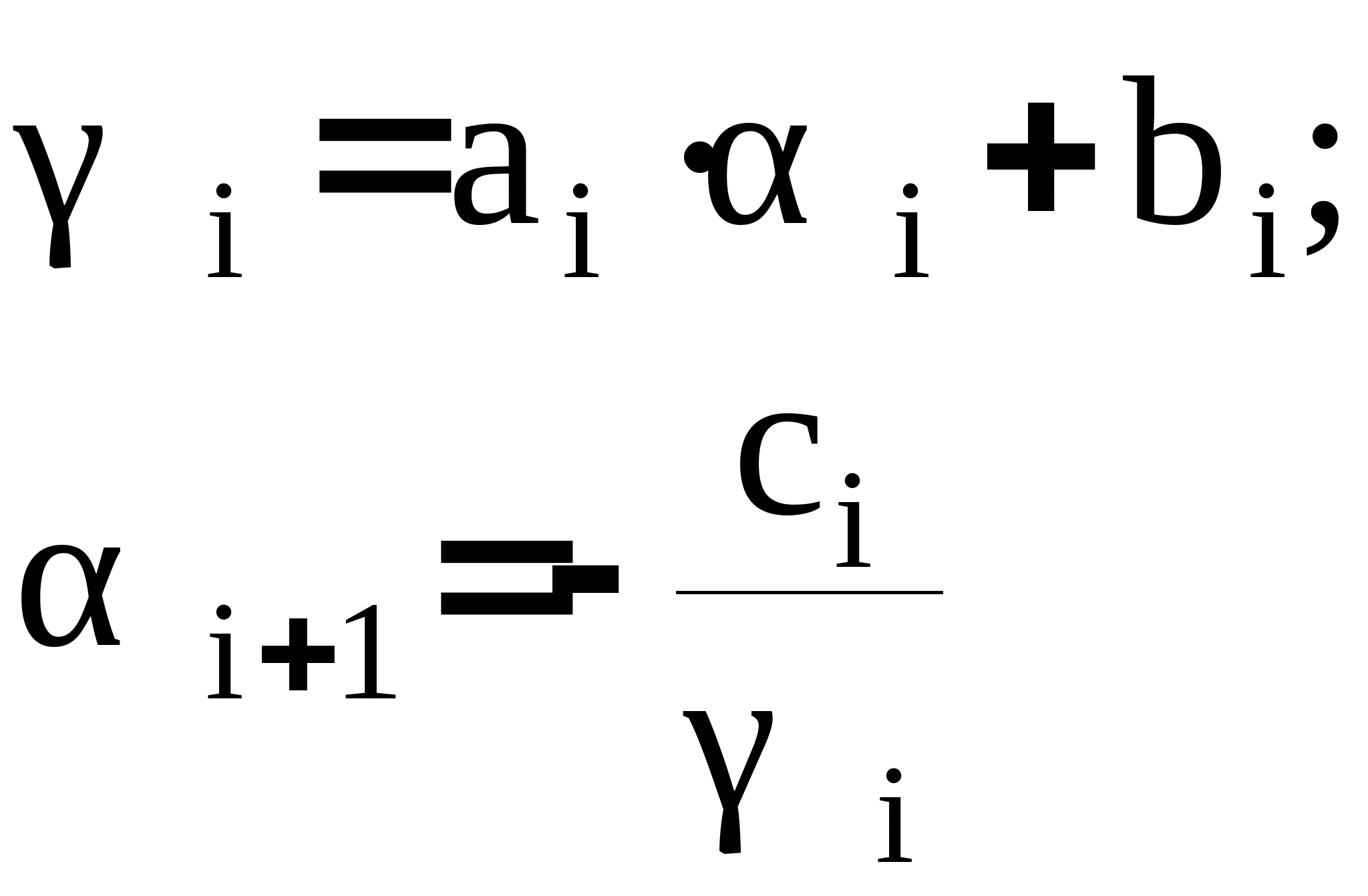

Обратный ход метода прогонки заключается в нахождении неизвестных xn, xn-1, ... x1. Он начинается с равенства: xn=bn+1; 
const max=10; type matrix=array[1..max] of real; matrix_2=array[0..max] of real;
procedure input_matr(var a:matrix;n:byte;c:char); var i:byte; begin for i:=1 to n do begin writeln('Введите ',i ,'-ый элемент массива ',c); readln(a[i]) end end;
procedure process(a,b,c,d:matrix;var x:matrix;n:byte); var alfa,betta:matrix_2; gamma,fi:matrix; i:byte; begin betta[0]:=0; alfa[0]:=0; for i:=1 to n do begin gamma[i]:=b[i]+a[i]*alfa[i-1]; fi[i]:=d[i]-a[i]*betta[i-1]; alfa[i]:=-c[i]/gamma[i]; betta[i]:=fi[i]/gamma[i] end; x[n]:=betta[n]; for i:=n-1 downto 1 do x[i]:=alfa[i]*x[i+1]+betta[i] end;
procedure out_matr_x(a:matrix;n:byte); var i:byte; begin for i:=1 to n do writeln(i ,' корень уравнения равен ',a[i]:5:3) end;
var i:byte; a,b,c,d,x,gamma,fi:matrix; alfa,betta:matrix_2; n:byte; begin writeln('Введите размерность системы '); readln(n); if (n>=2) and (n<=10) then begin input_matr(a,n,'a'); input_matr(b,n,'b'); input_matr(c,n,'c'); input_matr(d,n,'d'); process(a,b,c,d,x,n); out_matr_x(x,n) end else writeln('1< Размерность <=10 !!! ') end.
Результат работы программы:
1 корень уравнения равен 0.526 2 корень уравнения равен 0.628 3 корень уравнения равен 0.640 4 корень уравнения равен 1.200
ЛАБОРАТОРНАЯ РАБОТА №9 «Методы решения систем линейных уравнений ». Студента группы ПВ-22 Малютина Максима.
Задание. Методом Зейделя решить систему линейных уравнений с точностью до 0,001.
С истема : истема :
Для решения системы уравнений методом Зейделя необходимо выполнения условия диагонального преобладания, после приведения к данному виду система имеет вид: 
В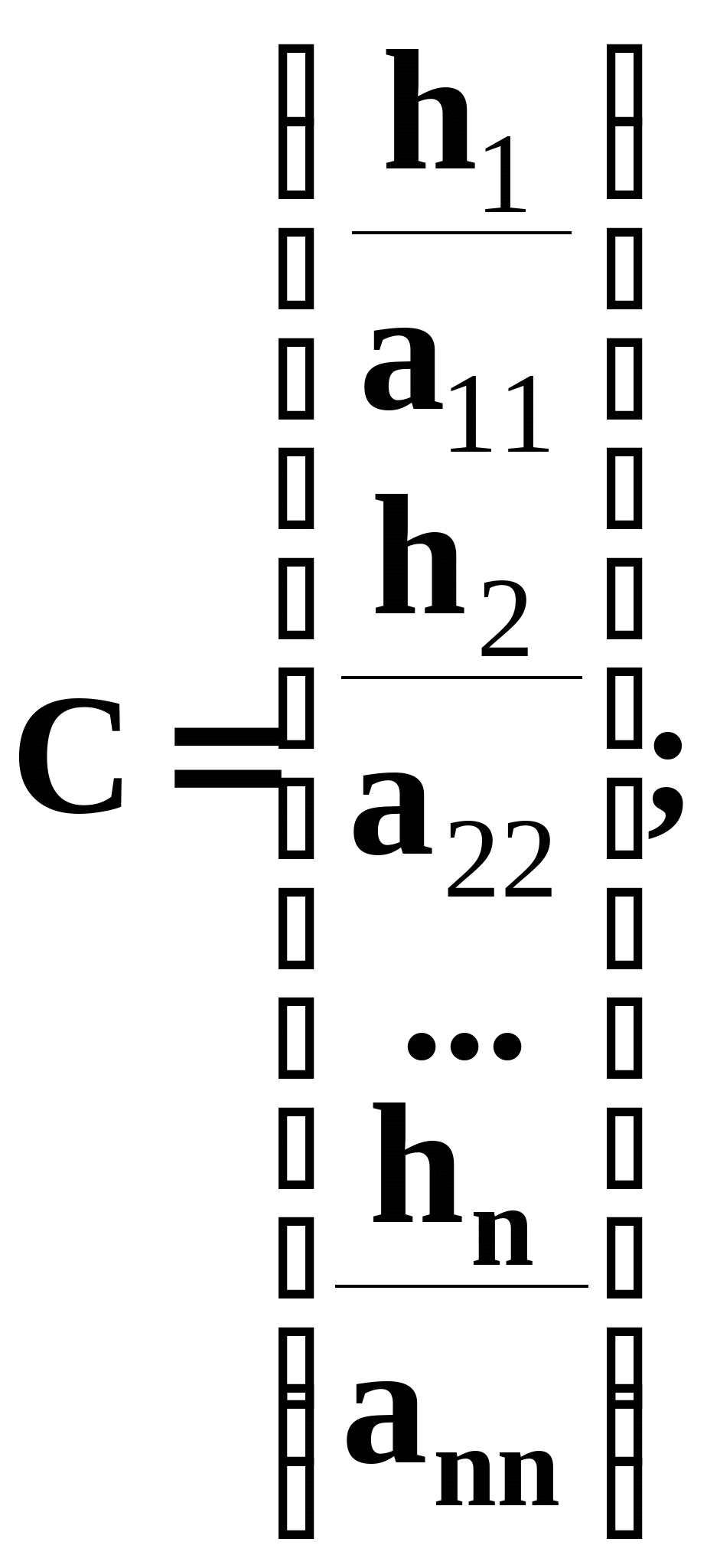
оспользуемся разложением матрицы А на В и С вида: 
  Далее найдем решение приближенное решение уравнения следующим способом: Правило остановки: Далее найдем решение приближенное решение уравнения следующим способом: Правило остановки:
Из норм матрицы В выбирается меньшая, нормы вектора и матрицы согласованны между собой. При вычислении приближения следующей координаты используются более точные значения предыдущих координат текущего приближения. const size=10; type vector=array[1..size] of real; matrix=array[1..size] of vector; norma=function(a:matrix;n:byte):real; norma_v=function(a:vector;n:byte):real;
Procedure InputVector(var a:vector;n:byte); var i:byte; begin for i:=1 to n do begin writeln('Введите ',i,'-ый элемент '); readln(a[i]); end; end;
Procedure InputMatrix(var a:matrix;n:byte); var i:byte; begin for i:=1 to n do begin writeln('Введите ',i,'-ую строку матрицы '); InputVector(a[i],n) end; end;
Procedure OutputVector(var a:vector;n:byte); var i:byte; begin for i:=1 to n do write(a[i]:10:5); writeln end;
Procedure OutputMatrix(var a:matrix;n:byte); var i:byte; begin for i:=1 to n do outputvector(a[i],n) end;
Procedure GetB(var b:matrix;a:matrix;n:byte); var i,j:byte; s:real; begin for i:=1 to n do for j:=1 to n do if i<>j then b[i,j]:=-a[i,j]/a[i,i] else b[i,j]:=0; end;
Procedure GetC(var c:vector;h:vector;n:byte;a:matrix); var i:byte; begin for i:=1 to n do c[i]:=h[i]/a[i,i] end;
Function Norma_1v(a:vector;n:byte):real; var i:byte; s:real; begin s:=a[1]; for i:=2 to n do if abs(a[i])>s then s:=abs(a[i]); norma_1v:=s end;
Function Norma_8v(a:vector;n:byte):real; var i:byte; s:real; begin s:=0; for i:=1 to n do s:=s+abs(a[i]); norma_8v:=s end;
Function Norma_1(a:matrix;n:byte):real; var s,norma:real; i,j:byte; begin norma:=0; for j:=1 to n do begin s:=0; for i:=1 to n do s:=s+abs(a[i,j]); if s>norma then norma:=s end; norma_1:=norma end;
Function Norma_8(a:matrix;n:byte):real; var s,norma:real; i,j:byte; begin norma:=0; for i:=1 to n do begin s:=0; for j:=1 to n do s:=s+abs(a[i,j]); if s>norma then norma:=s end; norma_8:=norma end;
procedure MulMatrix(a:matrix;ma,na:byte;b:matrix;mb,nb:byte;var c:matrix;var mc,nc:byte); var i,j,k:byte; s:real; begin if na=nb then begin mc:=ma; nc:=nb; for k:=1 to mc do for j:=1 to nc do begin s:=0; for i:=1 to nc do s:=s+a[k,i]*b[i,j]; c[k,j]:=s end; end else begin writeln('Неверные размеры матриц !!! '); halt end; end;
Procedure SubMatr(a:matrix;var b:matrix;n:byte); var i,j:byte; begin for i:=1 to n do for j:=1 to n do b[i,j]:=a[i,j]-b[i,j] end;
procedure MulVector(a:matrix;ma,na:byte;b:vector;nb:byte;var c:vector;var nc:byte); var i,j:byte; s:real; begin if na=nb then begin nc:=nb; for i:=1 to nc do begin s:=0; for j:=1 to nc do s:=s+a[i,j]*b[j]; c[i]:=s; end; end else begin writeln('Неверные размеры !!! '); halt end; end;
procedure MulVectorZ(a:matrix;n:byte;var b:vector); var i,j:byte; s:real; begin for i:=1 to n do begin s:=0; for j:=1 to n do s:=s+a[i,j]*b[j]; b[i]:=s; end; end;
Procedure SubVect(a,b:vector;var c:vector;n:byte); var i:byte; begin for i:=1 to n do c[i]:=b[i]-a[i] end;
Procedure AddVect(a:vector;var b:vector;n:byte); var i:byte; begin for i:=1 to n do b[i]:=b[i]+a[i] end;
var a,b,bn:matrix; h,c,xr,x,xn:vector; i,n:byte; eps:real; nor:norma; norv:norma_v;
begin writeln('Введите размерность матрицы коэффициентов ');readln(n); writeln('Введите элементы матрицы коэффициентов '); InputMatrix(a,n); writeln('Введите вектор свободных членов H '); InputVector(h,n); writeln('Введите заданныю точность '); readln(eps); GetB(b,a,n); GetC(c,h,n,a); writeln('Матрица B: '); OutputMatrix(b,n); writeln('Вектор C: '); OutputVector(c,n); readln; if (norma_1(b,n)<=norma_8(b,n)) and (norma_1(b,n)<>0) then begin nor:=norma_1; norv:=norma_1v end else begin nor:=norma_8; norv:=norma_8v end; eps:=eps*(1-nor(b,n))/nor(b,n); for i:=1 to n do x[i]:=1; MulVectorZ(b,n,x); AddVect(c,x,n); xn:=x; MulVectorZ(b,n,xn); AddVect(c,xn,n); subvect(x,xn,xr,n); while norv(xr,n)>eps do begin x:=xn; MulVectorZ(b,n,xn); AddVect(c,xn,n); subvect(x,xn,xr,n) end; writeln('Значения X '); OutputVector(x,n); MulVector(a,n,n,x,n,c,n); writeln('Проверка '); OutputVector(c,n); end.
Результат работы программы:
Матрица B: 0.00000 0.06250 -0.11458 -0.34375 0.00000 -0.26563 -0.45946 -0.32432 0.00000
Вектор C: -0.08333 1.26563 0.25676
Значения X 0.01836 1.30590 -0.17513
Проверка -0.79990 8.10045 1.90065 |