Курсовая работа: Малошумящие однозеркальные параболические антенны

РЕСПУБЛИКА КАЗАХСТАН

АЛМАТИТНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

ФАКУЛЬТЕТ РАДИОТЕХНИКИ И СВЯЗИ

Кафедра Радиотехники

Курсовая работа

на тему: “Малошумящие однозеркальные параболические антенны”

Алматы 2008

ТЕХНИЧЕСКОЕ ЗАДАНИЕ

Рабочая частота f, ГГц

Ширина ДН на уровне половины мощности 2Q_0,5 ^Н , мрад

Ширина ДН на уровне половины мощности 2Q_0,5 ^Е , мрад …

Уровень боковых лепестков, дБ

Средняя яркостная температура неба Т_НСР , ^° К

Температура шумов приёмника Т_пр , ^° К

Длина фидерной линии l_ф , м

Тип облучателя

Открытый конец прямоугольного волновода

СОДЕРЖАНИЕ

Техническое задание

Содержание

Введение

1. Расчет геометрических и электродинамических параметров облучателя и параболоида:

a) выбор фидера. Определение шумовой температуры фидерного тракта;

b) определение диаметра раскрыва;

c) аппроксимация аналитического вида ДН облучателя функцией вида

cos^{n /2} Y;

d) определение угла раскрыва и фокусного расстояния зеркальной антенны.

2. Расчет геометрических и электродинамических характеристик поля:

a) диаграммы направленности облучателя;

b) распределение поля в апертуре зеркала.

3. Расчет пространственной диаграммы направленности и определение параметров параболической антенны.

4. Конструктивный расчет антенны:

a) расчет профиля зеркала;

b) выбор конструкции зеркала;

c) определение допусков на точность изготовления

Выводы

Список литературы

Приложение А

ВВЕДЕНИЕ

Параболические антенны в последнее время находят все более широкое применение в космических и радиорелейных линиях связи. В 1888 году известный немецкий физик Г. Герц в своих опытах по СВЧ оптике впервые применил в качестве фокусирующего устройства параболический цилиндр. Интерес к зеркальным антеннам не ослабевает и в наши дни в связи со стремительным развитием космических радиотехнических систем и комплексов. Достаточная простота и легкость конструкции, возможность формирования самых разнообразных диаграмм направленности, высокий КПД, малая шумовая температура – вот основные достоинства, зеркальных антенн, обуславливающих их широкое применение в современных радиосистемах. Целью данной курсовой является освоение методики проектирования зеркальных параболических антенн: определение их основных электродинамических параметров и конструктивный расчет. В курсовой работе определение поля излучения параболической антенны производится апертурным методом, который широко применяем при проектировании зеркальных антенн.

1. Расчет геометрических и электродинамических параметров облучателя и параболоида

a) выбор фидера. Определение шумовой температуры фидерного тракта

В качестве фидера будем использовать прямоугольный волновод для частоты f = 5 ГГц ([1], приложение А):

a x b = 4.0 x 2.0 (см);

a = 0.0431 (дБ/м).

Шумовая температура фидерного тракта Т_афу определяется по формуле:

,

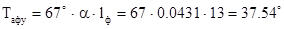где α – коэффициент затухания линии передачи [дБ/м],

l_ф – длина фидерной линии [м].

КПД определяется по формуле:

b) определение диаметра раскрыва

Зеркальная антенна – направленная антенна, содержащая первичный излучатель и отражатель антенны в виде металлической поверхности. Параболическая зеркальная антенна представлена на рисунке 1.

Рисунок 1 – Зеркальная параболическая антенна

В случае равномерно возбуждённого раскрыва параболического зеркала ширина ДН приближённо определяется:

,

где

2Q_0.5 – ширина диаграммы направленности на уровне половинной мощности, рад.;

l - длина волны излучаемого (принимаемого) антенной радиосигнала;

R₀ – радиус раскрыва зеркала (рисунок 1).

Длина волны определяется по формуле:

Неравномерное возбуждение раскрыва зеркала приводит к некоторому расширению главного лепестка ДН, так как уменьшается эффективная площадь раскрыва. Чаще всего диаграммы направленности зеркальных антенн не обладают осевой симметрией, т.е. ширина главного лепестка в плоскостях Е и Н различна. В большинстве практических случаев это влечёт за собой следующее изменени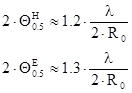е:

, где

2Q^Е _0.5 , 2Q^Н _0.5 ширина ДН соответственно в плоскостях Е и Н.

Для Е и Н плоскостей соответственно найдем радиус раскрыва:

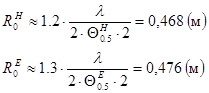
Т. к. в курсовой имеются данные о ширине диаграммы направленности в обеих плоскостях, можно определить диаметр раскрыва d_p = 2 × R₀ , причем из полученных двух значений диаметра следует выбрать наибольшее. Следовательно, R₀ = 0,476(м).

d_p = 2 × R₀ = 2 × 0,476 = 0,952 (м)

c) аппроксимация аналитического вида ДН облучателя функцией вида cos^{n /2} Y

В зависимости от размещения облучателя относительно зеркала можно получить то или иное значение КНД. При определенном оптимальном отношении R_o /f_o КНД наибольший. Это объясняется тем, что количество теряемой энергии зависит от формы диаграммы направленности облучателя и от отношения R_o /f_o . При уменьшении отношения R_o /f_o от оптимального КНД уменьшается, так как увеличивается часть энергии, проходящей мимо зеркала. С другой стороны, увеличение этого отношения также приводит к уменьшению КНД в связи с более сильным отклонением закона распределения возбуждения от равномерного; оптимальное значение R_o /f_o определяется по аппроксимированной нормированной ДН облучателя (аппроксимация функцией вида F(q)=cos^{n / 2} (q), где n определяет степень вытянутости ДН облучателя). Для облучателя в виде пирамидального рупора n = 6 ([1], таблица 4.1).

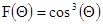
d) определение угла раскрыва и фокусного расстояния зеркальной антенны

С точки зрения оптимизации геометрии антенны по максимальному отношению сигнал/шум необходимо произвести следующий расчет.

Чувствительность g определяется по формуле:

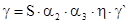
Где первые четыре коэффициента не зависят от y_о , а g^' вычисляется:

, где

Т₁ = Т_пр + Т₀ × (1 - η) + η × Т_нср = 1500 × 290 × (1 – 0.871) + 0.871 × 5 = 1542 К

Т_о = 290 К;

u = (0.02 – 0.03) – коэффициент, учитывающий «переливание» части мощности облучателя через края зеркала;

u = 0.025;

S = π × R² = 3.14 × 0,476 = 0,712 м² , площадь апертуры зеркала;

n = 6 – определяется типом облучателя;

a₁ = 1 - cos^{n +1} Y₀ ;

σ_а /2R = 0.4 × 10^-4 – точность профиля зеркала.

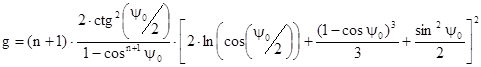
Построим график функции γ`(Y₀ ), по максимуму которого определим угол раскрыва зеркала.

График 1 – График функции γ`(Y₀ )

Y₀ = 0.82 (рад) = 46,983° Þ a₁ = 0,931, g = 0,877, g` = 5,216×10 ^–4 .

Фокусное расстояние f может быть найдено из следующего соотношения:

В зависимости от размещения облучателя относительно зеркала можно получить то или иное значение КНД. При определенном оптимальном отношении R₀ /f₀ КНД наибольший. Заданный интервал отношения R₀ /f₀ = (0.8÷1.0). Расчетное отношение R₀ /f₀ = 0.89, что удовлетворяет условию.

Определим шумовую температуру антенной системы:

2. Расчет геометрических и электродинамических характеристик поля

a) диаграммы направленности облучателя

Расчет сводиться к определению геометрических размеров облучателя, при которых уменьшение амплитуды поля на краю раскрыва зеркала происходит до одной трети амплитуды поля в центре раскрыва, и диаграммы направленности облучателя.

Рисунок 3 – открытый конец прямоугольного волновода

ДН рупорной антенны рассчитываются по формулам:

в Е плоскости

в Н плоскости , где

β₀ = 2×π/λ – волновое число

-аппроксимация аналитического вида ДН облучателя

Т.к. Ro-радиус раскрыва зеркала, был вычислен по приблизительной формуле он не удовлетворяет вычислениям, вследствие чего я выбрал Ro=0,407 (м) удовлетворяющий дальнейшим вычислениям.

d_p = 2 × R₀ = 2 × 0,407= 814 (м);

S = π × R² = 3.14 × 0,407 = 1,52 м² , площадь апертуры зеркала;

График 2– ДН облучателя (открытый конец прямоугольного волновода)

b) распределение поля в апертуре зеркала

Расчет распределения поля в апертуре зеркала осуществляется по следующим формулам:

, где

F₀ (Y) – диаграмма направленности облучателя, Y₀ – угол раскрыва, Y - текущий угол.

, где

f₀ – фокусное расстояние.

График 3 – Распределение поля в апертуре зеркала

В данном случае Y₀ – текущий угол, а Y - сдвиг фаз между токами.

3. Расчет пространственной диаграммы направленности и определение параметров параболической антенны

Инженерный расчёт пространственной диаграммы направленности ДН параболической антенны часто сводится к определению ДН идеальной круглой синфазной площадки с неравномерным распределением напряжённости возбуждающего поля. В данном случае распределение напряжённости возбуждающего поля в основном определяется ДН облучателя в соответствующей плоскости. Выражение для нормированной ДН зеркальной параболической антенны при этом имеет вид:

,

где J₁ , J₂ – цилиндрические функции Бесселя первого и второго порядка.

,

где

Е_кр , Е_мах – амплитуды поля на краю и в центре раскрыва.

Коэффициент, показывающий во сколько раз амплитуда возбуждающего поля, на краю раскрыва меньше амплитуды в центре раскрыва в соответствующей плоскости с учётом различий расстояний от облучателя до центра зеркала и до края зеркала;

Построим ДН зеркальной параболической антенны:

a) для плоскости Н

График 4 – Пространственная ДН в плоскости Н

b) для плоскости Е

График 5 – Пространственная ДН в плоскости Е

Уровень боковых лепестков.

Для плоскости Е

Для плоскости Н

Приближенно коэффициент направленного действия зеркальной антенны определяется выражением:

,

где

S – площадь раскрыва;

υ_рез – результирующий коэффициент использования поверхности

Коэффициент использования поверхности:

Эффективная площадь антенны:

Коэффициент направленного действия:

Коэффициент усиления антенны:

4. Конструктивный расчет антенны

a) Расчет профиля зеркала

Зеркальные антенны имеют наибольший КНД при синфазном возбуждении раскрыва (плоский фазовый фронт волны). Параболический профиль зеркала обеспечивает одинаковые длины электрических путей от облучателя, установленного в фокусе параболоида вращения, до каждой точки плоскости раскрыва (свойство параболы). В полярной системе координат парабола описывается уравнением

,

где

r, Y - полярные координаты;

f - фокусное расстояние;

Y изменяется от 0 до Y₀ .

График 6– Плоский фазовый фронт волны

b) Выбор конструкции зеркала

С целью уменьшения веса и ветровых нагрузок поверхность зеркала часто выполняется перфорированной, или сетчатой

Рисунок 3 – Конструкция зеркала

При такой конструкции зеркала часть энергии просачивается сквозь него, образую нежелательное излучение. Допустимым является значение коэффициента прохождения в обратном направлении.

,

где

Р_пад , Р_обр – мощность излучения падающего на зеркало и в обратном направлении, соответственно.

Двухлинейная сетка работает удовлетворительно при расстоянии между проводниками меньше 0.1l и диаметре проводов не менее 0.01l.

d_п = 0.1 × 0.06 = 0.006 (м);

d = 0.01 × 0.06 = 0.0006 (м).

c) Определение допусков на точность изготовления

Неточность изготовления зеркала вызывает несинфазность поля в раскрыве. Допустимыми являются фазовые искажения поля в раскрыве зеркала не более ± p/4. При этом уменьшение коэффициента усиления антенны не превышает нескольких процентов.

Пусть поверхность параболоида имеет некоторые неровности (выступы и углубления). Наибольшее отклонение от идеальной поверхности в направлении r обозначим через Δr.

Рисунок 4 – Допуски на точность изготовления зеркала

Путь луча, отраженного от неровности в месте наибольшего отклонения от r изменяется при этом на величину Dr + Dr × cosY, а соответствующий сдвиг фаз составит величину Dj = b×Dr×(1+cosY), и он не должен превышать величину p/4, отсюда получаем

Анализ полученного выражения для Dr показывает, что вблизи центра параболоида (Y = 0) необходимая точность изготовления зеркала наивысшая. Здесь наибольшее отклонение от идеальной поверхности не должно превосходить величины l/16 (т.е. 0.013) у кромки параболоида требования к точности получаются наименьшими. Точность установки облучателя также определяется нормами на наибольшие допустимые фазовые искажения поля в раскрыве. Пусть фазовый облучатель смещен на Dх. Тогда длины путей лучей от фазового центра до раскрыва увеличиваются. Наибольшее удлинение пути происходит у лучей, падающих на вершину зеркала. Это удлинение путей при малых смещениях можно приблизительно определить как Dх×cosY. Тогда изменение фазы составит величину

,

где

Dj₀ , Dj_а – фазовые искажения_, возникающие из-за неточности установки облучателя, в центре и на краю раскрыва, соответственно. Эта величина не должна превышать p/4, отсюда получаем:

Таким образом, с увеличением угла раскрыва точность и установка облучателя в фокусе повышается.

Выводы

В результате проведенной работы сравним полученные данные с исходными:

Исходные данные:

2Q^Н _0.5 = 77 мрад - ширина ДН на уровне половинной мощности в плоскости Н

2Q^Е _0.5 = 82 мрад - ширина ДН на уровне половинной мощности в плоскости Е

УБЛ = -29 дБ – уровень боковых лепестков

Рассчитанные данные:

- уровень боковых лепестков в плоскости Н

- отклонение боковых лепестков в

плоскости Н от заданного значения

- уровень боковых лепестков в плоскости Е

- отклонение боковых лепестков в

плоскости Е от заданного значения

Полученная ширина ДН:

2Q^Н _0.5 = 81,4 мрад

2Q^Е _0.5 = 81 мрад

- отклонение в плоскости Н

- отклонение в плоскости Е

Отклонений в плоскости Н и Е незначительное.

Снижение уровня дальнего бокового излучения антенны обеспечивается прежде всего спадом амплитуды возбуждающего поля к краям раскрыва. Интенсивность дифракционного поля может быть оценена методом геометрической теории дифракции (ГТД).

Другой путь снижения поля в заднем полупространстве состоит в использовании специальных экранов, ослабляющих рассеянное поле. Этот способ можно проиллюстрировать на примере рупорной антенны. На рисунке 17 показана обычная рупорная антенна со специальными экранами. Экраны выполнены в виде части поверхности параболического цилиндра, фокальные линии которых совмещены с кромками рупора. В такой схеме заметно снижается уровень излучения в заднем полупространстве, но конструкция является слишком сложной. В зеркальных антеннах могут быть использованы более простые плоские экраны, как показано на рисунке 18,а и б. Использование одного экрана позволяет уменьшить уровень поля в заднем полупространстве на 8...14 дБ. Два последовательно расположенных экрана обеспечивают уменьшение уровня поля на 20... 25 дБ. Эти экраны могут выполняться из листового металла или густой проволочной сетки, причем жестких требований к точности выполнения и установки экранов не предъявляется.

Рисунок 17. Рупорная антенна.

Рисунок 18. Зеркальные антенны. Рисунок 19. Типы расфазирующих кромок

Третий путь снижения интенсивности дифракционных полей основан на деформации контура раскрыва антенны. Так, если контур раскрыва представляет окружность с центром, лежащим на фокальной оси параболоида, все токи контура возбуждаются синфазно, что обусловливает высокий уровень дифракционного поля в направлении 2=180°. Для уменьшения уровня этого поля необходимо придать кромке параболоида такую форму, при которой парциальные дифракционные поля, возбуждаемые отдельными участками кромок, были бы расфазированы в направлениях, близких к 2=180°. На рисунке 19 приведены различные типы расфазирующих кромок (спиральная, треугольная, лепестковая). Они уменьшают излучение в направлениях, близких к 2=180°, на 5... 6 дБ.

Четвертый путь снижения дальнего бокового излучения антенны связан с выполнением периферийной части поверхности раскрыва антенны из радиопо-глощающего или частично радиопрозрачного материала. Наиболее просто такой материал выполнить в виде металлического листа, поверхность которого перфорирована отверстиями. Изменяя размеры отверстий и их плотность расположения, можно добиться уменьшения интенсивности рассеянного поля.

В заключение отметим, что еще одним существенным фактором, определяющим дальнее боковое излучение антенн (впрочем, как и ближнее), является наличие статистических распределенных ошибок амплитудно-фазового распределения, обусловленных, например, технологическими погрешностями выполнения профиля зеркала.

Список литературы

1. Гончаров В.Л. Татлах А.Л. «Малошумящие однозеркальные параболические антенны и распространение радио волн», 1998;

2. Вознесенский Д.И. «Антенны. Современное состояние и проблемы», М: Советское радио, 1979;

3. Марков Г.Т. Сазанов Д. М. «Антенны», М: Энергия, 1975;

4. Кочержевский Г.М. «Антенно-фидерные устройства», М: Радио и связь, 1981;

5. Айзенберг Г.З. «Антенны ультракоротких волн», М: Связьиздат, 1957;

6. Хмель В.Ф. «Антенны и Устройства СВЧ», Киев 1976.