| Задача 1 (16.88)
Минимизировать функцию f(x) на всей числовой оси методом Ньютона. Критерием достижения требуемой точности считать выполнение неравенства 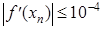 . .
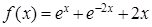
Решение:
Найдем первую и вторую производные исходной функции:
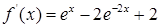
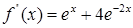
Выберем начальное приближение 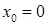 . И осуществим вычисления по формуле . И осуществим вычисления по формуле

Результаты запишем в таблице
| n
|
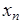
|
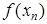
|
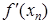
|
| 0
|
0
|
2
|
1
|
| 1
|
-0,2
|
1,91
|
-0,1649
|
| 2
|
-0,175697
|
1,908525
|
-0,0032
|
| 3
|
-0,17520305
|
1,908524
|
-0,0000013
|
n=1

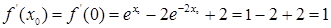
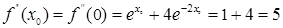
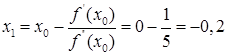
n=2
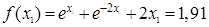
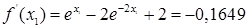
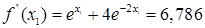

n=3
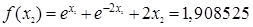
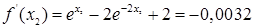
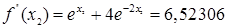

n=4
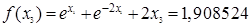
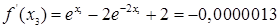
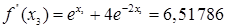

Далее мы заканчиваем вычисления, потому что данная точность 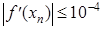 достигнута. В результате мы получаем: достигнута. В результате мы получаем: 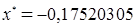 и и 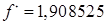 . .
Осуществим проверку при помощи встроенной функции Minimize:
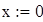
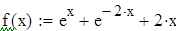 , ,
Ответ:
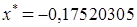 и и 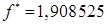
Задача 2 (16.115)
Выписать матрицу Q квадратичной функции f(x), найти ее градиент 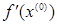 в точке в точке 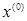 и убедиться в выпуклости f(x) в и убедиться в выпуклости f(x) в  . .
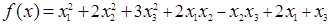 , , 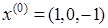
Решение:
Запишем исходную функцию в следующем виде:
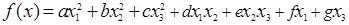 , ,
где 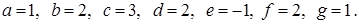
Тогда матрица Q примет вид:
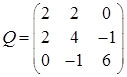
Найдем градиент 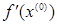 в точке в точке 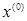 по формуле по формуле 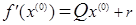 , где r – вектор-столбец и равен , где r – вектор-столбец и равен 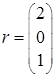 : :

Подставляя в полученную матрицу 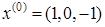 , мы получаем следующее значение градиента в данной точке: , мы получаем следующее значение градиента в данной точке:

Теперь убедимся в выпуклости f(x) в 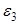 . Для того, чтобы исходная функция была выпуклой в . Для того, чтобы исходная функция была выпуклой в 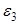 , достаточно, чтобы матрица Q была положительно определена. Для этого найдем угловые миноры , достаточно, чтобы матрица Q была положительно определена. Для этого найдем угловые миноры 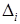 матрицы Q и если они будут больше нуля, то функция f(x) будет выпуклой в матрицы Q и если они будут больше нуля, то функция f(x) будет выпуклой в 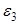 . .
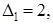 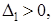
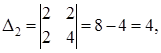 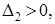
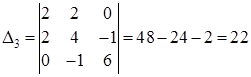 , , 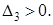
Так как 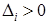 , , 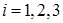 ,то функция f(x) выпукла в ,то функция f(x) выпукла в  . .
Проверка в
Mathcad
:


Проверка на выпуклость и нахождение градиента в точке x0
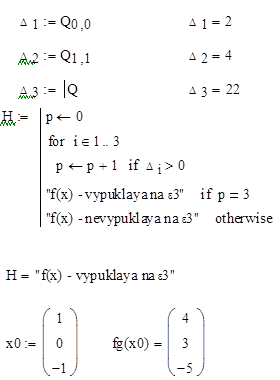
Ответ: градиент равен 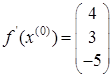 и функция f(x) будет выпуклой в и функция f(x) будет выпуклой в 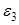 . .
Задача 3 (16.136)
Минимизировать квадратичную функцию методом наискорейшего спуска, заканчивая вычисления при 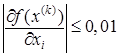 , , 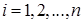 . .
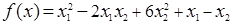
Решение:
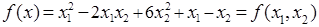
Тогда производные исходной функции будут иметь вид:

Выберем начальное приближение 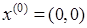 . Тогда . Тогда
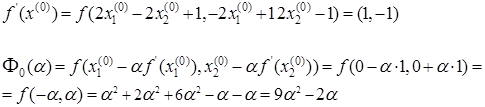
Для нахождения точки минимума функции 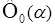 найдем нули ее производной: найдем нули ее производной:

Зная 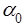 , мы определим , мы определим 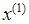 следующим образом: следующим образом:
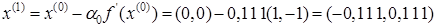
И так далее по выше описанной цепочке.
Реализуем решение данной задачи в математическом пакете Mathcad.
Функция имеет вид:
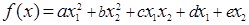
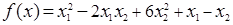
Тогда коэффициенты будут равны
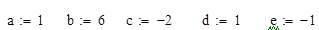
Возьмем следующие начальное приближение  и и  : :
Далее пишем программу
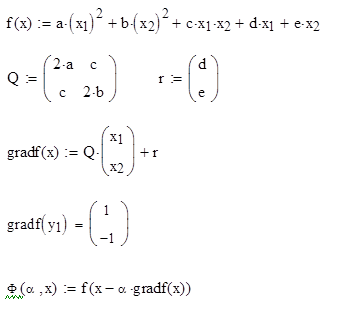
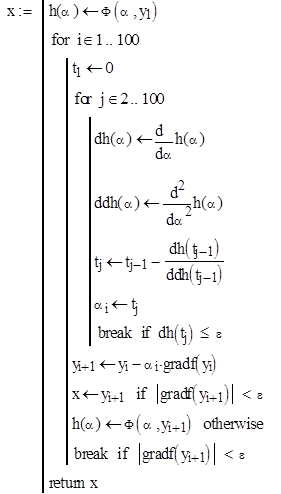
В результате получаем искомое решение 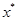 и функцию и функцию 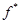 : :
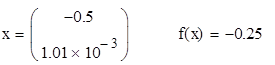
Ответ:
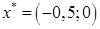 и и 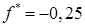
Задача 4 (16.155)
Минимизировать функцию f(x) методом сопряженных направлений, заканчивая вычисления при 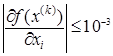 , , 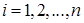 . .
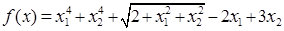
Решение:
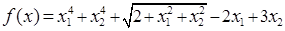
Тогда частные производные исходной функции будут иметь вид:
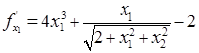
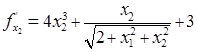
Решение будем искать по следующему алгоритму:

Шаг 1.
Выбрав начальное приближение
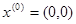 , , 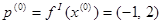
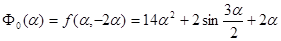
Для нахождения точки минимума функции 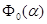 используем метод перебора: используем метод перебора:

=>> 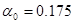 , откуда , откуда 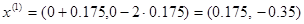
Шаг 2.
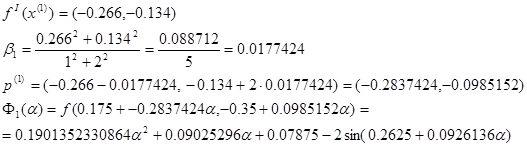
Для нахождения точки минимума функции  используем метод перебора: используем метод перебора:
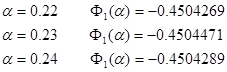
=>> 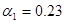 , ,
откуда
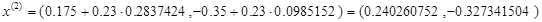
Шаг 3.
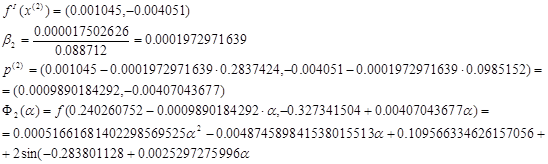
Для нахождения точки минимума функции 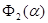 используем метод перебора: используем метод перебора:
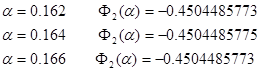
=>> 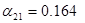 , откуда , откуда

Шаг 4.
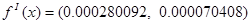
следовательно требуемая точность достигнута и
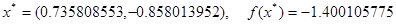
Ответ:
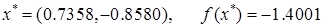
Задача 5 (16.193)
Решить задачу линейного программирования графическим методом.
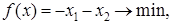
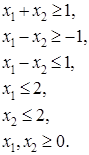
Решение:
Изобразим на плоскости 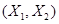 наш многоугольник ABCDE (красного цвета) и одну из линий уровня наш многоугольник ABCDE (красного цвета) и одну из линий уровня 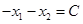 (розового цвета). (розового цвета).
Линии AB соответствует уравнение 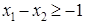 , BC соответствует , BC соответствует 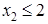 , CD соответствует , CD соответствует 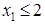 , DE соответствует , DE соответствует 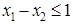 и EA соответствует и EA соответствует 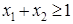
Направление убывания функции 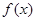 указывает вектор указывает вектор 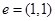 . Совершая параллельный перенос линии уровня вдоль направления . Совершая параллельный перенос линии уровня вдоль направления 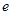 , находим ее крайнее положение. В этом положении прямая , находим ее крайнее положение. В этом положении прямая 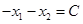 проходит через вершину проходит через вершину 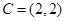 многоугольника ABCDE. Поэтому целевая функция многоугольника ABCDE. Поэтому целевая функция 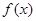 принимает минимальное значение принимает минимальное значение 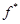 в точке в точке 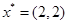 , причем , причем 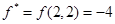
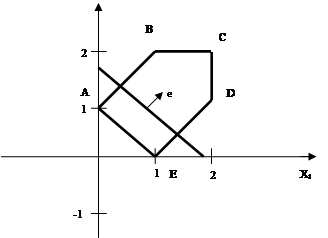 Ответ: 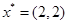 и и 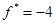
Задача 6 (16.205)
Решить задачу линейного программирования в каноническом виде графическим методом.
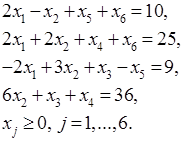
Решение:
Матрица системы будет иметь следующий вид:
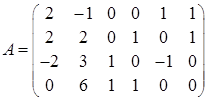
Ранг этой матрицы равен 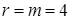 . Тогда число свободных переменных равно . Тогда число свободных переменных равно 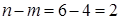 , поэтому для решения задачи можно использовать графический метод. Решив систему ограничений – равенств относительно базисных переменных , поэтому для решения задачи можно использовать графический метод. Решив систему ограничений – равенств относительно базисных переменных 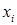 , , 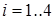 , получим: , получим:
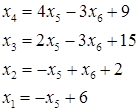
Исключая с помощью полученной системы переменные 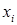 , , 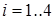 из выражения для целевой функции, получаем: из выражения для целевой функции, получаем:
С учетом условия неотрицательности  , ,  , и последних равенств получаем следующую задачу: , и последних равенств получаем следующую задачу:
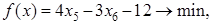
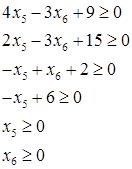 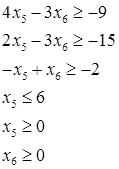
Изобразим на плоскости  наш многоугольник ABCDEJ (красного цвета) и одну из линий уровня наш многоугольник ABCDEJ (красного цвета) и одну из линий уровня 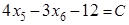 (розового цвета). (розового цвета).
Линии AB соответствует уравнение 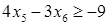 , BC соответствует , BC соответствует 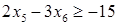 , CD соответствует , CD соответствует 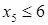 , DE соответствует , DE соответствует 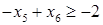 , EJ соответствует , EJ соответствует 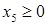 и JA соответствует и JA соответствует 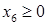 . .
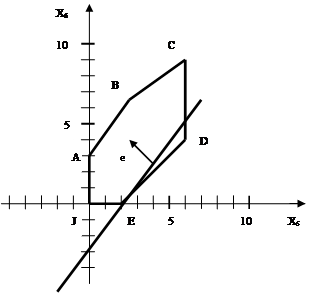
Направление убывания функции 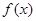 указывает вектор указывает вектор 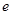 . Совершая параллельный перенос линии уровня вдоль направления . Совершая параллельный перенос линии уровня вдоль направления 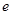 , мы видим, что целевая функция содержит сторону AB многоугольника ABCDEJ. Таким образом, все точки отрезка AB являются точками минимума функции , мы видим, что целевая функция содержит сторону AB многоугольника ABCDEJ. Таким образом, все точки отрезка AB являются точками минимума функции 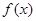 . Так как концы A и B имеют координаты . Так как концы A и B имеют координаты 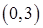 и и 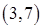 соответственно, то найдем отсюда координаты соответственно, то найдем отсюда координаты 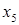 и и 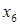 : :
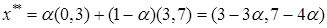
Тогда любая точка минимума  представима в виде представима в виде
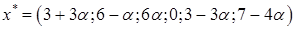
где 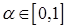 . Минимальное значение целевой функции . Минимальное значение целевой функции
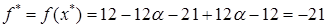
Ответ: бесконечное множество решений
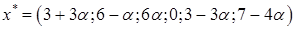 , где , где 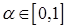 и и 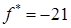 . .
Задача 7 (16.216)
Решить задачу линейного программирования симплекс - методом, находя начальную угловую точку методом искусственного базиса.
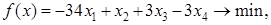
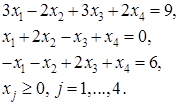
Решение:
Матрица системы имеет вид
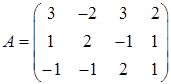 . .
Ее ранг равен 3. Введем дополнительные переменные 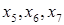 и запишем условие вспомогательной задачи линейного программирования для рассматриваемого случая: и запишем условие вспомогательной задачи линейного программирования для рассматриваемого случая:
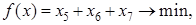
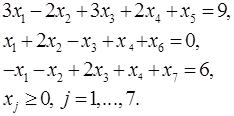
Считая дополнительные переменные 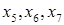 базисными, запишем симплекс таблицу этой задачи, соответствующую угловой точке базисными, запишем симплекс таблицу этой задачи, соответствующую угловой точке 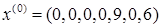 : :
| 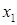
|
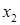
|
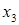
|
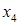
|
| 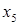
|
3
|
-2
|
3
|
2
|
9
|
| 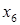
|
1
|
2
|
-1
|
1
|
0
|
| 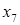
|
-1
|
-1
|
2
|
1
|
6
|
| -3
|
1
|
-4
|
-4
|
-15
|
Произведем преобразования исходной симплекс-таблицы симплекс-методом следующим образом:
1) смотрим на нижнюю строку – выбираем тот столбец, в котором нижний элемент отрицательный, если таких столбцов несколько, то выбираем любой (в нашем случае выбираем первый столбец 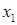 ); );
2) далее смотрим на последний и выбранный столбцы – сравниваем отношения элементов последнего и выбранного столбцов (в выбранном столбце берем только положительные числа), и выбираем тот элемент выбранного столбца, где отношение элементов будет наименьшим (в нашем случае 9/3 и 0/1, так как второе отношение наименьшее, следовательно, опорным элементом будет 1);
3) меняем местами переменные 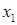 и и 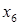 , остальные переменные оставляем на своих местах; , остальные переменные оставляем на своих местах;
4) на место опорного элемента ставим отношение 1/(опорный элемент);
5) на остальных местах разрешающей строки записываем соответствующие элементы исходной таблицы, деленные на опорный элемент;
6) на свободные места разрешающего столбца ставим со знаком минус соответствующие элементы исходной таблицы, деленные на опорный элемент;
7) оставшиеся свободные места в новой симплекс-таблице заполняем построчно следующим образом: из строки элементов исходной таблицы вычитаем произведение ее элемента из разрешающего столбца на уже заполненную разрешающую строку новой таблицы.
Производя преобразования симплекс-метода, получим такую последовательность симплекс-таблиц:
| 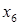
|
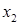
|
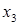
|
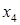
|
| 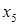
|
-3
|
-8
|
6
|
-1
|
9
|
| 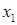
|
1
|
2
|
-1
|
1
|
0
|
| 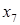
|
1
|
1
|
1
|
2
|
6
|
| 3
|
7
|
-7
|
-1
|
-15
|
| 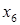
|
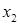
|
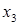
|
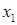
|
| 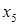
|
-2
|
-6
|
5
|
1
|
9
|
| 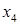
|
1
|
2
|
-1
|
1
|
0
|
| 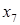
|
-1
|
-3
|
3
|
-2
|
6
|
| 4
|
9
|
-8
|
1
|
-15
|
| 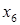
|
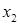
|
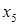
|
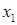
|
| 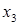
|
-2/5
|
-6/5
|
1/5
|
1/5
|
9/5
|
| 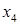
|
3/5
|
4/5
|
1/5
|
6/5
|
9/5
|
| 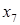
|
1/5
|
3/5
|
-3/5
|
-13/5
|
3/5
|
| 4/5
|
-3/5
|
8/5
|
13/5
|
-3/5
|
| 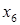
|
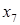
|
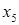
|
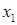
|
| 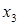
|
0
|
2
|
-1
|
-5
|
3
|
| 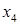
|
1/3
|
-4/3
|
1
|
14/3
|
1
|
| 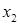
|
1/3
|
5/3
|
-1
|
-13/3
|
1
|
| 1
|
1
|
1
|
0
|
0
|
В нижней строке последней симплекс-таблицы нет отрицательных элементов, следовательно, минимум вспомогательной целевой функции достигнут и 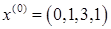 есть угловая точка допустимого множества исходной задачи линейного программирования, тогда есть угловая точка допустимого множества исходной задачи линейного программирования, тогда
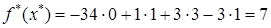
Ответ: 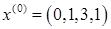 и и 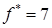 . .
Задача 8 (16.237)
Решить полностью целочисленную задачу линейного программирования методом Гомори.
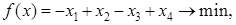
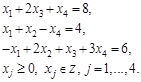
Решение:
Введем дополнительные переменные 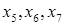 и запишем условие вспомогательной задачи линейного программирования для рассматриваемого случая: и запишем условие вспомогательной задачи линейного программирования для рассматриваемого случая:
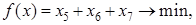
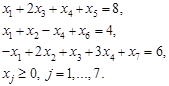
Считая дополнительные переменные 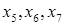 базисными, запишем симплекс таблицу этой задачи, соответствующую угловой точке базисными, запишем симплекс таблицу этой задачи, соответствующую угловой точке 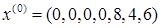 : :
| 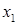
|
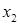
|
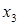
|
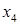
|
| 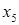
|
1
|
0
|
2
|
1
|
8
|
| 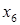
|
1
|
1
|
0
|
-1
|
4
|
| 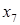
|
-1
|
2
|
1
|
3
|
6
|
| -1
|
-3
|
-3
|
-3
|
-18
|
Произведем преобразования исходной симплекс-таблицы симплекс-методом следующим образом: смотрим на нижнюю строку – выбираем тот столбец, в котором нижний элемент отрицательный, если таких столбцов несколько, то выбираем любой (в нашем случае выбираем первый столбец 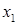 ); далее смотрим на последний и выбранный столбцы – сравниваем отношения элементов последнего и выбранного столбцов (в выбранном столбце берем только положительные числа), и выбираем тот элемент выбранного столбца, где отношение элементов будет наименьшим (в нашем случае 9/3 и 0/1, так как второе отношение наименьшее, следовательно, опорным элементом будет 1); меняем местами переменные ); далее смотрим на последний и выбранный столбцы – сравниваем отношения элементов последнего и выбранного столбцов (в выбранном столбце берем только положительные числа), и выбираем тот элемент выбранного столбца, где отношение элементов будет наименьшим (в нашем случае 9/3 и 0/1, так как второе отношение наименьшее, следовательно, опорным элементом будет 1); меняем местами переменные 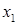 и и 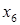 , остальные переменные оставляем на своих местах; на место опорного элемента ставим отношение 1/(опорный элемент); а остальных местах разрешающей строки записываем соответствующие элементы исходной таблицы, деленные на опорный элемент; на свободные места разрешающего столбца ставим со знаком минус соответствующие элементы исходной таблицы, деленные на опорный элемент; оставшиеся свободные места в новой симплекс-таблице заполняем построчно следующим образом: из строки элементов исходной таблицы вычитаем произведение ее элемента из разрешающего столбца на уже заполненную разрешающую строку новой таблицы. Производя преобразования симплекс-метода, получим такую последовательность симплекс-таблиц: , остальные переменные оставляем на своих местах; на место опорного элемента ставим отношение 1/(опорный элемент); а остальных местах разрешающей строки записываем соответствующие элементы исходной таблицы, деленные на опорный элемент; на свободные места разрешающего столбца ставим со знаком минус соответствующие элементы исходной таблицы, деленные на опорный элемент; оставшиеся свободные места в новой симплекс-таблице заполняем построчно следующим образом: из строки элементов исходной таблицы вычитаем произведение ее элемента из разрешающего столбца на уже заполненную разрешающую строку новой таблицы. Производя преобразования симплекс-метода, получим такую последовательность симплекс-таблиц:
| 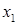
|
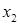
|
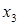
|
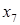
|
| 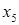
|
4/3
|
-2/3
|
5/3
|
-1/3
|
6
|
| 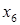
|
2/3
|
5/3
|
1/3
|
1/3
|
6
|
| 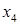
|
-1/3
|
2/3
|
1/3
|
1/3
|
2
|
| -2
|
-1
|
-2
|
1
|
-12
|
| 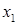
|
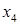
|
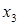
|
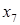
|
| 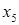
|
1
|
1
|
2
|
0
|
8
|
| 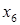
|
3/2
|
-5/2
|
-1/2
|
-1/2
|
1
|
| 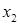
|
-1/2
|
3/2
|
1/2
|
1/2
|
3
|
| -5/2
|
3/2
|
-3/2
|
3/2
|
-9
|
| 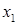
|
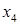
|
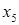
|
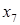
|
| 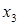
|
1/2
|
1/2
|
1/2
|
0
|
4
|
| 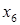
|
7/4
|
-9/4
|
1/4
|
-1/2
|
3
|
| 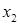
|
-3/4
|
5/4
|
-1/4
|
1/2
|
1
|
| -7/4
|
9/4
|
3/4
|
3/2
|
-3
|
| 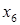
|
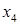
|
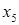
|
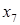
|
| 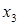
|
-2/7
|
8/7
|
3/7
|
1/7
|
22/7
|
| 
|
4/7
|
-9/7
|
1/7
|
-2/7
|
12/7
|
| 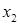
|
3/7
|
2/7
|
-1/7
|
2/7
|
16/7
|
| 1
|
0
|
1
|
1
|
0
|
Как видим, в последней строке таблицы все элементы положительны, то есть получаем решение  и и  . Но это решение не удовлетворяет условию целочисленности, поэтому дополняем последнюю симплекс-таблицу строкой, используя следующие правила: среди нецелых элементов . Но это решение не удовлетворяет условию целочисленности, поэтому дополняем последнюю симплекс-таблицу строкой, используя следующие правила: среди нецелых элементов  выбирается произвольный элемент выбирается произвольный элемент  , по r
-ой строке симплекс-таблицы составляется дополнительное ограничение вида , по r
-ой строке симплекс-таблицы составляется дополнительное ограничение вида  (здесь мы полагаем, что свободные переменные (здесь мы полагаем, что свободные переменные  имеют номера m
+1,…,
n
). С помощью вспомогательной переменной имеют номера m
+1,…,
n
). С помощью вспомогательной переменной  это ограничение представляется в виде равенства это ограничение представляется в виде равенства  и вводится в симплекс-таблицу дополнительной строкой и вводится в симплекс-таблицу дополнительной строкой

Где
 , ,
где фигурные скобки означают дробную часть.
Таким образом, мы получаем следующую таблицу:
| 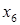
|
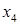
|
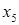
|
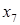
|
| 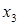
|
-2/7
|
8/7
|
3/7
|
1/7
|
22/7
|
| 
|
4/7
|
-9/7
|
1/7
|
-2/7
|
12/7
|
| 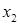
|
3/7
|
2/7
|
-1/7
|
2/7
|
16/7
|
| 
|
2/7
|
-1/7
|
-3/7
|
-1/7
|
-1/7
|
| 1
|
0
|
1
|
1
|
0
|
Так как  , то после дополнения строкой симплекс-таблица перестает соответствовать допустимому базисному решению задачи линейного программирования, которую она описывает. , то после дополнения строкой симплекс-таблица перестает соответствовать допустимому базисному решению задачи линейного программирования, которую она описывает.
Для перехода к допустимому базисному решению производятся следующие операции:
а) строка с отрицательным свободным членом  считается разрешающей; считается разрешающей;
б) если все коэффициенты  , то задача не имеет решения, в противном случае номер l
разрешающего столбца находится из условия: , то задача не имеет решения, в противном случае номер l
разрешающего столбца находится из условия:

в) совершается преобразование симплекс-таблицы с опорным элементом 
Если в новой таблице по-прежнему есть хотя бы один отрицательный свободный член, то описанная процедура повторяется, начиная с операции а), необходимое число раз.
Применяя данные правила к нашей симплекс-таблице, мы получаем следующие преобразования:
| 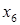
|
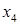
|
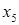
|
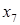
|
| 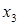
|
-2/7
|
8/7
|
3/7
|
1/7
|
22/7
|
| 
|
4/7
|
-9/7
|
1/7
|
-2/7
|
12/7
|
| 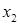
|
3/7
|
2/7
|
-1/7
|
2/7
|
16/7
|
| 
|
2/7
|
-1/7
|
-3/7
|
-1/7
|
-1/7
|
| 1
|
0
|
1
|
1
|
0
|
| 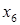
|

|
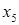
|
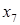
|
| 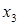
|
2
|
8
|
-3
|
-1
|
2
|
| 
|
-2
|
-9
|
4
|
1
|
3
|
| 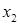
|
1
|
2
|
-1
|
0
|
2
|
| 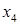
|
-2
|
-7
|
3
|
1
|
1
|
| 1
|
0
|
1
|
1
|
0
|
Полученная симплекс-таблица не только соответствует допустимому базисному решению, но и дает решение рассматриваемой задачи:
 и и 
Ответ:  и и 
Задача 9 (16.258)
Решить задачу дробно - линейного программирования.


Знаменатель  целевой функции положителен при всех x
из допустимого множества U, так как целевой функции положителен при всех x
из допустимого множества U, так как  . .
Вводим новые переменные
 , ,  , , 
и получаем следующую задачу линейного программирования:

 
Неизвестные параметры мы можем уже из этих выражений найти:
 
   , ,
Ответ:  , , 
Задача 10 (16.268)
Решить задачу квадратичного программирования.
 , ,

Решение:
Матрица  нашей квадратичной функции положительно определена. Наша исходная задача имеет вид: нашей квадратичной функции положительно определена. Наша исходная задача имеет вид:
 (1) (1)
 , ,  , (2) , (2)
 , ,  . (3) . (3)
На основании теоремы Куна-Таккера точка минимума  целевой функции целевой функции  из (1) на допустимом множестве (2) и (3) может быть найдена как решение следующей системы уравнений с дополнительными переменными из (1) на допустимом множестве (2) и (3) может быть найдена как решение следующей системы уравнений с дополнительными переменными  ; ;  : :
 , ,  , ,
 , ,  , ,
 , ,  , ,
 , ,  , ,
удовлетворяющее условию неотрицательности:
 , ,  , ,  , ,
 , ,  . .
Применяя выше описанные условия, мы преобразуем исходную задачу в следующий вид:

Будем искать угловую точку множества, определяемого этой системой, методом искусственного базиса. Введем дополнительные переменные  и и  в 3-е и 4-ое уравнения выше написанной системы, считая базисными переменными начальной угловой точки в 3-е и 4-ое уравнения выше написанной системы, считая базисными переменными начальной угловой точки  , ,  , , 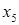 и и  . .
Вспомогательную целевую функцию  выразим через свободные переменные выразим через свободные переменные  , , 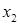 , ,  , ,  , ,  и и  с помощью двух первых уравнений выше написанной системы. с помощью двух первых уравнений выше написанной системы.
Последовательность симплекс-таблиц, приводящих к решению задачи, приведена ниже. Рамками обведены опорные элементы, а те свободные переменные, которые на данном шаге нельзя переносить в базисные из-за условий  , обведены кружками. , обведены кружками.


Как видим, в последней строчке нет отрицательных чисел, следовательно, мы нашли решение и оно имеет вид  и и  . .
Ответ:  и и 
|