Бабаев Х.
Об одном аналоге задачи Бицадзе-Самарского
для смешанно-составного уравнения.
РЕФЕРАТ
В данной работе для смешанно-составного уравнения ставится и исследуется одна нелокальная краевая задача, которая является некоторым аналогом задачи Бицадзе-Самарского. Единственность решения изучаемой задачи доказывается принципом максимума, а существование решения доказывается сведением изучаемой задачи к эквивалентному ей интегральному уравнению.
Библиография 4 названия
Об одном аналоге задачи Бицадзе-Самарского
для смешанно-составного уравнения
В первые в работе [1] была поставлена и иcследована нелокальная краевая задача для элиптического уравнения, которая является обобщением задачи Дириxле. В данной работе иcследуется один из аналогов этой задачи для уравнения.
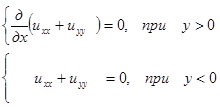
Пусть: Д область ограниченная отрезками OB, BE, AE, OC, AC, прямыxx=0, y=1, x=1, x+y=0, x-y=1, где А, B, O, C, E точки с координатами (1;0), (0;1), (0;0), (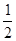 ; ;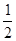 ), (1;1) соответственно. ), (1;1) соответственно.
Задача.
Найти регулярное в области Д/OА решение уравнения (1) довлетворяющее краевым
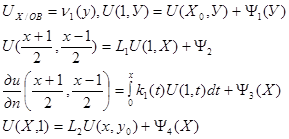 (2) (2)
(3)
(4)
(5)
условиям и условиям склеивания
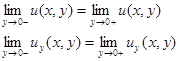 (6) (6)
Где 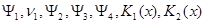 -задание функции, причем -задание функции, причем 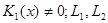 -известные постоянные; постоянная β удовлетворяет неравенству -известные постоянные; постоянная β удовлетворяет неравенству 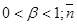 -внутренняя нормаль. -внутренняя нормаль.
Любое регулярное решение уравнения (1) в области
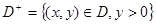 представлено в виде представлено в виде
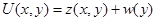 (7) (7)
где z(X,У)-регулярное решение уравнения
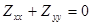 (8) (8)
W (y)-дважды непрерывно дифференцируемая функция.
Без ограничения общности можно предположить, что W (0)=0б W (1)=0, сперва приводим доказательство единственности решения изучаемой задачи.
Теорема
. Если 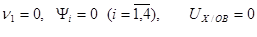 то функция U (Х,У)=0 в области Д. то функция U (Х,У)=0 в области Д.
Доказательство.
На основании (2), (7) задача редуцируется к определению регулярного решения уравнения (8) при У>0 удовлетворяющего краевым условиям
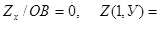 φ(У)-W(У), Z( φ(У)-W(У), Z(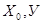 )=φ(У)-W(У) )=φ(У)-W(У)
где U(1,У)= φ(У), U(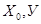 )=φ(У) (9) )=φ(У) (9)
Из (6) следует
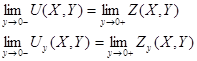
Учитывая (3) и условие (9) получим:
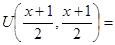 L L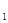 φ(x) φ(x)
общее решение уравнения (1) в области Д ={(x,y)Є D, y<0}даётся известной формулой Даламбера ={(x,y)Є D, y<0}даётся известной формулой Даламбера
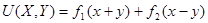
реализуя условие (10) из (11) имеем
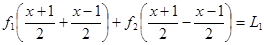 φ(x) φ(x)
или 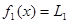 φ(x)- φ(x)-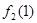
отсюда 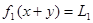 φ(x+y)- φ(x+y)-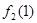
тогда из (11) получим U(X,Y)=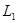 φ(X+Y)- φ(X+Y)-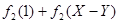 (12) (12)
Используя (4) (ψ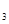 (X)≡0) из (12) найдем (X)≡0) из (12) найдем
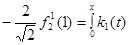 φ φ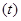 d d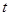 + +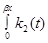 φ φ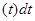 (13) (13)
дифференцируя выражение (13) имеем
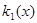 φ φ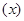 + +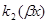 φ φ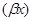 =0 =0
разделяя на 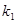 (x)≠0 получим (x)≠0 получим
φ(x)+ φ φ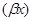 =0 (14) =0 (14)
предпологая
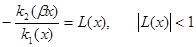
имеем:φ(x)-L(x) φ(βx)=0 (15)
функциональное уравнение (15) не имеет нетривиальных решений.
Действительно применяя метод итерации находим
φ(х)=L(х)φ(βx)
φ(βx)=L(βx)·φ(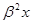 ) )
φ(β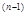 x)=L(β x)=L(β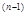 x) φ(β x) φ(β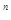 x) x)
из этих равенств имеем
φ(х)=L(x)L(βx)…L(β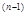 x)φ(β x)φ(β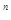 x) (16) x) (16)
(0≤x≤1)
из (16) следует, что при n→∞ функция φ(х)≡0
Следовательно из (12) получим
U(X,Y)= -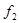 (1)+ (1)+ 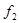 (X-Y) (X-Y)
Отсюда 
Или 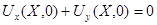
Обозначим U(X,1)=ψ(X). тогда условие (5) примет вид
U(x,y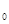 )= )=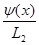
Следовательно из (7)
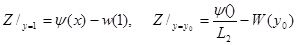
теперь нетрудно убедиться, что функция Z(X,Y) не достигает максимума на линии У=1. Из условий
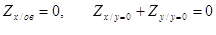
следует, что Z(X,Y) не достигает максимума (минимума) и на отрезках OB и OA.
Функция Z(Х,Y) не достигает максимума (минимум) и на отрезке АЕ. Действительно, если Z(X,Y) достигает максимума (минимума) на АЕ, то из условия Z(X ,Y)=φ(Y)-W(Y) ,Y)=φ(Y)-W(Y)
Следует, что этот максимум (минимум) должен реализоваться и внутри области, что противоречит известным свойствам решений элиптических уравнений.
Итак Z(X,Y) ≡ 0 в области Д , W(Y) ≡ 0 при 0≤Y≤1. U ≡ 0 и в области Д , W(Y) ≡ 0 при 0≤Y≤1. U ≡ 0 и в области Д (Задача Коши). (Задача Коши).
Таким образом U(X,Y)≡0 в области Д.
Теперь переходим к доказательству существования решения изучаемой задачи.
Реализуя условие (3) имеем:
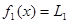 φ(x)+ψ φ(x)+ψ (x)- (x)-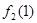
тогда из (11) получим
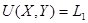 φ(Х+У)+ψ φ(Х+У)+ψ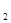 (Х+Y)- (Х+Y)-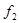 (1)+ (1)+ 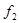 (X-Y) (18) (X-Y) (18)
используя условие (4) после простых преобразований приходим к функциональному уравнению.
Φ(х)-L(x)φ(βx)=δx (19)
Где δ(x)=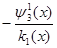
Единственное решение функционального уравнения (19) можно найти применением метода итерации.
Таким образом неизвестная функция φ(х) определена единственным образом. Из (18) найдём
U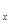 (X,0)+U (X,0)+U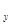 (X,0)= (X,0)=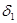 (X) (20) (X) (20)
Где известная функция
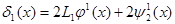
регулярное в области Д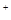 решение уравнения (8) удовлетворяющее краевым решение уравнения (8) удовлетворяющее краевым
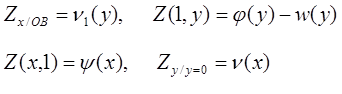 условиям условиям
задается формулой [2]:
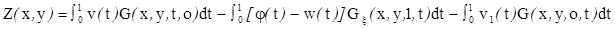
Отсюда находим 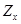 (X,0): (X,0):
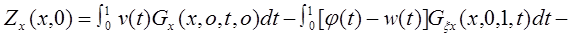
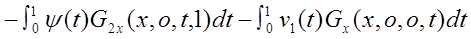 22) 22)
исключая 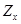 (х,о) из формул (20), (22) для определения V(х) получаем интегральное уравнение Фредгольма второго рода, разрешимость которого следует из единственности решения изучаемой задачи. (х,о) из формул (20), (22) для определения V(х) получаем интегральное уравнение Фредгольма второго рода, разрешимость которого следует из единственности решения изучаемой задачи.
Заметим что V(x) содержит неизвестные функции ψ(Х), W(У). Подставляя значение V(Х) в формулу (21) и реализуя краевые условия
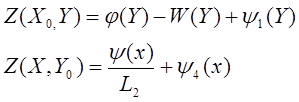
.Для определения неизвестных функций ψ(Х), W(У) имеем систему интегральных уравнений Фредгольма второго рода, которая однозначно разрешима.
Литература.
1. Бицадзе А. И., Самарский А. А. о некоторых простейших обобщениях простейших линейных элиптических краевых задач. –Докл. АН СССР, 1969 Т 189, N4, -c.739-740.
2. Базаров Д. О некоторых нелокальных краевых задачах для модельных уравнений уравнений второго порядка. –изв. вузов. Математика, 1990, N3.
3. Джураев Т. Д. Краевые задачи для уравнений смешанного и смешанно-составного типов. Ташкент: ФАН, 1979-238с
4. Салахидинов М. С., Толипов А. Некоторые краевые задачи для уравнений смешанного типа с одной и двумя линиями вырождения. //Дифференциальные уравнения, 1972 г. Т. 8, №1 c 134-142
|