Задание
Таблица 1
| Пенсия, тыс. руб., у |
131 |
110 |
170 |
141 |
150 |
160 |
200 |
230 |
240 |
260 |
270 |
300 |
| Прожиточный минимум тыс. руб., х |
100 |
90 |
150 |
31 |
60 |
39 |
40 |
70 |
80 |
150 |
120 |
130 |
Построить линейное регрессионное уравнение.
1. Построить поле корреляции и линию регрессии на одном графике.
Вычислить:
2. коэффициент детерминации;
3. среднюю ошибку аппроксимации;
4. t-статистики;
5. доверительные интервалы.
6. Сделать выводы
Построить показательную зависимость и повторить пункты 1–6.
Сравнить построенные модели.
Решение:
Построим поле корреляции:
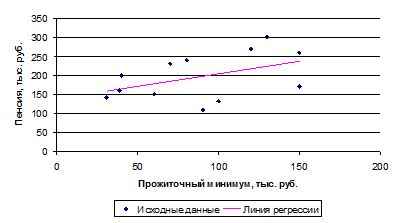
Рис. 1. Поле корреляции пенсии от прожиточного минимума
По полю корреляции слабо прослеживается зависимость пенсии от прожиточного минимума.
Рассчитаем параметры уравнения линейной парной регрессии.
Для расчета параметров a и b уравнения линейной регрессии у = а + bx решим систему нормальных уравнений относительно а и b:
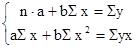
По исходным данным рассчитываем Sх, Sу, Sух, Sх2
, Sу2
.
Таблица 2
| № п/п |
y |
x |
yx |
x2
|
y2
|
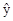 |
у –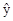 |
(у –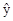 )2 )2
|
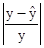 |
| 1 |
131 |
100 |
13100 |
10000 |
17161 |
204,61 |
-73,61 |
5418,432 |
0,562 |
| 2 |
110 |
90 |
9900 |
8100 |
12100 |
197,94 |
-87,94 |
7733,444 |
0,799 |
| 3 |
170 |
150 |
25500 |
22500 |
28900 |
237,96 |
-67,96 |
4618,562 |
0,400 |
| 4 |
141 |
31 |
4371 |
961 |
19881 |
158,587 |
-17,587 |
309,303 |
0,125 |
| 5 |
150 |
60 |
9000 |
3600 |
22500 |
177,93 |
-27,93 |
780,085 |
0,186 |
| 6 |
160 |
39 |
6240 |
1521 |
25600 |
163,923 |
-3,923 |
15,390 |
0,025 |
| 7 |
200 |
40 |
8000 |
1600 |
40000 |
164,59 |
35,41 |
1253,868 |
0,177 |
| 8 |
230 |
70 |
16100 |
4900 |
52900 |
184,6 |
45,4 |
2061,160 |
0,197 |
| 9 |
240 |
80 |
19200 |
6400 |
57600 |
191,27 |
48,73 |
2374,613 |
0,203 |
| 10 |
260 |
150 |
39000 |
22500 |
67600 |
237,96 |
22,04 |
485,762 |
0,085 |
| 11 |
270 |
120 |
32400 |
14400 |
72900 |
217,95 |
52,05 |
2709,203 |
0,193 |
| 12 |
300 |
130 |
39000 |
16900 |
90000 |
224,62 |
75,38 |
5682,144 |
0,251 |
| Итого |
2362 |
1060 |
221811 |
113382 |
507142 |
2361,94 |
0,1 |
33441,964 |
3,203 |
| Среднее |
196,83 |
88,33 |
18484,25 |
9448,5 |
42261,83 |
| Обозначение среднего |
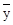 |
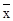 |
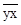 |
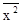 |
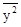 |
Найдем дисперсию переменных:
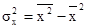 = 9448,5 – 88,332
= 1646,31 (тыс. руб.)2 = 9448,5 – 88,332
= 1646,31 (тыс. руб.)2
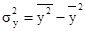 = 42261,83 – 196,832
= 3519,78 (тыс. руб.)2 = 42261,83 – 196,832
= 3519,78 (тыс. руб.)2
Найдем параметры a и b уравнения линейной регрессии:
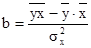 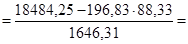 0,667 0,667
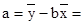 196,83 – 0,667 · 88,33 = 137,91 тыс. руб. 196,83 – 0,667 · 88,33 = 137,91 тыс. руб.
Уравнение регрессии:
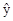 = 137,91 + 0,667 · х = 137,91 + 0,667 · х
Построим линию регрессии на рис. 1.
С увеличением прожиточного минимума на 1 тыс. руб. пенсия увеличивается на 0,667 тыс. руб.
Рассчитаем линейный коэффициент парной корреляции:
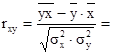 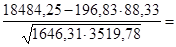 0,456 0,456
Т.к. коэффициент в интервале от 0,3 до 0,7 связь средняя, прямая.
Определим коэффициент детерминации:
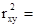 (0,456)2
= 0,208 (0,456)2
= 0,208
Т.е. вариация пенсий на 20,8% объясняется вариацией прожиточного минимума.
Найдем среднюю ошибку аппроксимации:
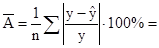 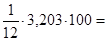 26,7% 26,7%
Средняя ошибка аппроксимации имеет значение меньше 30% – это говорит о среднем уровне надежности уравнения регрессии.
Рассчитаем F-критерий:
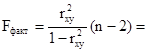 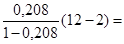 2,628 2,628
Критическое значение распределения Фишера определяют либо по таблицам распределения Фишера, либо расчетным путем с использованием функции FРАСПОБР() табличного процессора Excel. Для уровня доверия 0,95, одного фактора и 12 значений:
Fкр
= F(0,05; 1; 10) = 4,964
Т.к. Fкр
> Fфакт
, то необходимо отклонить гипотезу о статистической значимости параметров уравнения. Т.е. использовать данную функцию для аппроксимации нельзя.
Найдем стандартную ошибку остаточной компоненты по формуле:
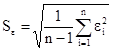 = = 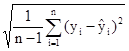 = = 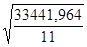 = 55,14 = 55,14
Найдем средние квадратичные (стандартные) ошибки оценивания коэффициента b и свободного члена а уравнения регрессии:
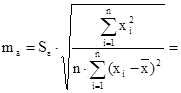 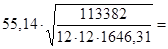 39,99 39,99
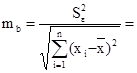 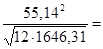 0,411 0,411
Найдем t – критерий Стьюдента для обоих параметров:
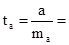 137,91 / 39,99 = 3,448 137,91 / 39,99 = 3,448
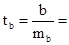 0,667 / 0,411 = 1,623 0,667 / 0,411 = 1,623
Сравнивая значения t-статистики для каждого из коэффициентов линейной регрессии с табличным значением (α = 0,05; k = 12) tтабл
= 2,228, можно сказать, что с вероятностью 95% коэффициент а надёжен, коэффициент b ненадёжен при данном уровне значимости.
Для расчета доверительного интервала определяем предельную ошибку Δ:
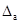 = tтабл
· = tтабл
· 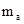 = 2,228 * 39,99 » 89,1 = 2,228 * 39,99 » 89,1
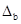 = tтабл
· = tтабл
· 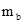 = 2,228 * 0,411 » 0,916 = 2,228 * 0,411 » 0,916
Доверительные интервалы для коэффициентов регрессии:
a – Δa
< a < a + Δa
48,81 < a < 227,01
b – Δb
< b < b + Δb
– 0,249 < b < 1,583
Таким образом, полученные оценки коэффициента регрессии b не являются эффективными и состоятельными, а само уравнение 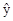 = 137,91 + 0,667·х не может использоваться для моделирования и прогнозирования динамики. = 137,91 + 0,667·х не может использоваться для моделирования и прогнозирования динамики.
Это обусловлено большой ошибкой уравнения регрессии.
Для построения уравнения показательной кривой у = а · еb
х
линеризуем переменные логарифмированием обеих частей уравнения:
ln у = ln а + b·x
Y = A + b·x
ГдеY = ln y, A = ln a.
Для расчетов будем использовать данные таблицы 4.
Таблица 4
| № |
y |
Y |
x |
Yx |
x2
|
Y2
|
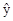 |
у –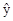 |
(у – 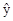 )2 )2
|
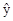 – – 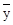 |
(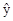 - -
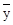 )2 )2
|
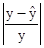 |
| 1 |
131 |
4,875 |
100 |
487,52 |
10000 |
23,7675 |
194,81 |
-63,81 |
4071,1 |
-2,025 |
4,1 |
0,487 |
| 2 |
110 |
4,700 |
90 |
423,043 |
8100 |
22,0945 |
188,78 |
-78,78 |
6206,8 |
-8,047 |
64,7 |
0,716 |
| 3 |
170 |
5,136 |
150 |
770,37 |
22500 |
26,3764 |
227,92 |
-57,92 |
3354,9 |
31,091 |
966,7 |
0,341 |
| 4 |
141 |
4,949 |
31 |
153,412 |
961 |
24,4902 |
156,86 |
-15,86 |
251,5 |
-39,972 |
1597,8 |
0,112 |
| 5 |
150 |
5,011 |
60 |
300,638 |
3600 |
25,1065 |
171,81 |
-21,81 |
475,8 |
-25,018 |
625,9 |
0,145 |
| 6 |
160 |
5,075 |
39 |
197,932 |
1521 |
25,7574 |
160,85 |
-0,85 |
0,7 |
-35,982 |
1294,7 |
0,005 |
| 7 |
200 |
5,298 |
40 |
211,933 |
1600 |
28,0722 |
161,35 |
38,65 |
1493,5 |
-35,476 |
1258,6 |
0,193 |
| 8 |
230 |
5,438 |
70 |
380,666 |
4900 |
29,5727 |
177,29 |
52,71 |
2778,1 |
-19,538 |
381,7 |
0,229 |
| 9 |
240 |
5,481 |
80 |
438,451 |
6400 |
30,0374 |
182,95 |
57,05 |
3255,0 |
-13,882 |
192,7 |
0,238 |
| 10 |
260 |
5,561 |
150 |
834,102 |
22500 |
30,9212 |
227,92 |
32,08 |
1029,0 |
31,091 |
966,7 |
0,123 |
| 11 |
270 |
5,598 |
120 |
671,811 |
14400 |
31,3423 |
207,43 |
62,57 |
3914,8 |
10,601 |
112,4 |
0,232 |
| 12 |
300 |
5,704 |
130 |
741,492 |
16900 |
32,5331 |
214,05 |
85,95 |
7387,8 |
17,218 |
296,5 |
0,287 |
| Итого |
2362 |
62,83 |
1060 |
5611,37 |
113382 |
330,0715 |
2272,02 |
90,0 |
34219,0 |
-89,938 |
7762,4 |
3,109 |
| Среднее |
196,83 |
5,235 |
88,33 |
467,614 |
9448,5 |
27,506 |
| Обозначение среднего |
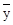 |
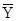 |
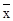 |
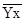 |
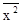 |
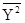 |
Найдем дисперсию переменных:
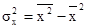 = 9448,5 – 88,332
= 1646,31 = 9448,5 – 88,332
= 1646,31
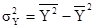 = 27,506 – 5,2352
= 0,0955 = 27,506 – 5,2352
= 0,0955
Найдем параметров А и В регрессии составили:
b =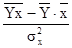 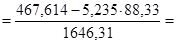 0,00314 0,00314
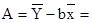 5,325 – 0,00314 · 88,33 = 4,958 5,325 – 0,00314 · 88,33 = 4,958
Получено линейное уравнение:
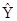 = 4,958 + 0,00314 · х = 4,958 + 0,00314 · х
Произведем потенцирование полученного уравнения и запишем его в обычной форме:
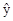 = e4,958
· e0,00314 · х
= 142,31 · e0,00314 х = e4,958
· e0,00314 · х
= 142,31 · e0,00314 х
Тесноту связи оценим через индекс корреляции рху
:
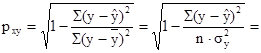 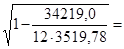 0,436 0,436
Связь средняя.
Определим коэффициент детерминации:
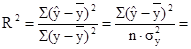 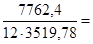 0,1838 0,1838
Т.е. вариация результативного признака на 18,38% объясняется вариацией факторного признака.
Найдем среднюю ошибку аппроксимации:
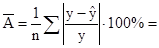 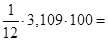 25,9% 25,9%
Средняя ошибка аппроксимации имеет значение меньше 30%, т.е. надежность уравнения средняя.
Рассчитаем F-критерий: (m – число параметров при переменной x)
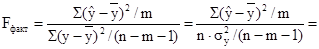 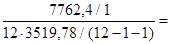 1,8378 1,8378
Fкр
= 4,964
Т.к. Fкр
> Fфакт
, т.е. необходимо отклонить гипотезу о статистической значимости параметров уравнения.
Найдем стандартную ошибку остаточной компоненты по формуле:
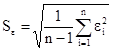 = = 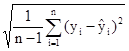 = = 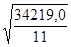 = 55,77 = 55,77
Найдем средние квадратичные (стандартные) ошибки оценивания коэффициента b и свободного члена а уравнения регрессии:
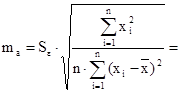 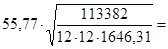 40,45 40,45
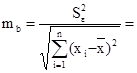 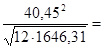 0,416 0,416
Найдем t – критерий Стьюдента для обоих параметров:
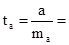 142,31 / 40,45 = 3,518 142,31 / 40,45 = 3,518
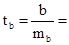 0,00314 / 0,411 = 0,0076 0,00314 / 0,411 = 0,0076
Сравнивая значения t-статистики для каждого из коэффициентов линейной регрессии с табличным значением (α = 0,05; k = 12) tтабл
= 2,228, можно сказать, что с вероятностью 95% коэффициент а надёжен, коэффициент b ненадёжен при данном уровне значимости.
Для расчета доверительного интервала определяем предельную ошибку Δ:
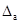 = tтабл
· = tтабл
· 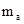 = 2,228 * 40,45 » 90,12 = 2,228 * 40,45 » 90,12
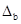 = tтабл
· = tтабл
· 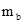 = 2,228 * 0,0076 » 0,0169 = 2,228 * 0,0076 » 0,0169
Доверительные интервалы для коэффициентов регрессии:
a – Δa
< a < a + Δa
52,19 < a < 232,43
b – Δb
< b < b + Δb
– 0,01376 < b < 0,02004
Построим линию показательной зависимости на поле корреляции:
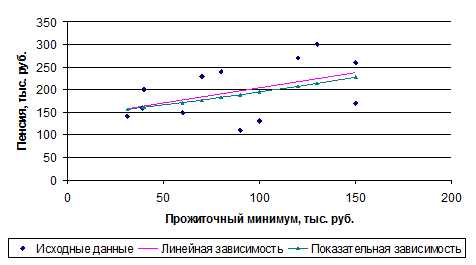
Рис. 2. Рассчитанные линии регрессий
У линейной зависимости меньше стандартная ошибка и больше значение F-критерия. Поэтому из двух уравнений регрессий линейное более достоверно. Но низкая надежность коэффициента регрессии b, говорит, что результаты аппроксимации будут иметь достаточно низкую надежность (80%).
|