КОНТРОЛЬНАЯ РАБОТА ПО ЭЛЕКТРОДИНАМИКЕ:
«Электромагнитные волны между параллельными идеально проводящими плоскостями»
Введение
На больших расстояниях от антенны электромагнитное поле имеет характер сферической волны. При движении такой волны в точку, где находится потребитель энергии (приемное устройство), естественно, попадает лишь незначительная часть общей энергии, излучаемой антенной. Иными словами, коэффициент полезного действия передачи электромагнитной энергии, т.е. отношение мощности, извлекаемой из пространства приемным устройством, к мощности, излученной передающей антенной, получается очень низким.
Устройства, в которых распространяются направляемые волны, получили название направляющих устройств или направляющих систем. В большинстве случаев они образованы поверхностями проводников; однако при некоторых условиях направляющими свойствами обладают также поверхности Диэлектриков. Следовательно, электромагнитные волны в направляющих системах движутся вдоль граничных поверхностей, выполняющих функции своеобразных «электромагнитных рельсов».
Направляющие устройства имеют самые разнообразные применения в современной радиотехнике. Наиболее широко они используются в качестве линий передачи или фидеров, предназначенных для передачи электромагнитной энергии из одной точки пространства в другую (например, от передатчика к антенне или от антенны к приемнику и т.п.) с высоким к. п.д.
1. Электромагнитные волны между параллельными идеально проводящими плоскостями
Для того чтобы найти поля, которые могут существовать в пространстве между проводящими плоскостями, необходимо решить уравнения Максвелла в заданной области при соответствующих граничных условиях.
Руководствуясь приведенными выше соображениями, мы будем полагать, что направляющие плоскости обладают бесконечно большой проводимостью. Тогда касательная составляющая вектора 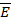 на этих плоскостях должна обращаться в нуль на этих плоскостях должна обращаться в нуль
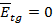 (1.1) (1.1)
Для решения уравнений Максвелла введем прямоугольную систему координат (рис. 1). В этой системе уравнения направляющих поверхностей запишутся самым простым образом: х = 0 и х = а.

Рис. 1 - Направляющая система, образованная двумя параллельными проводящими плоскостями
Предположим, что источники поля находятся вне пределов интересующей нас области и что волны распространяются по оси z. Будем также считать, что векторы 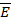 и и 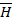 искомого поля не зависят от координаты искомого поля не зависят от координаты 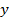 (двумерная задача). (двумерная задача).
Рассмотрим уравнения Максвелла:
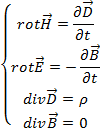
где: 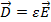 , , 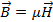 , , 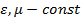 . .
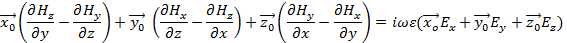
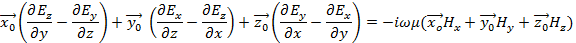

В рассматриваемой задаче волны распространяются вдоль оси OZ поэтому 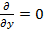 , отсюда: , отсюда:
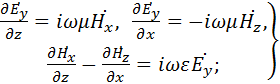 (1.2) (1.2)
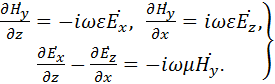 (1.3) (1.3)
Здесь 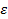 и и 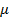 - параметры среды в пространстве между плоскостями (проводимость среды g равна нулю). - параметры среды в пространстве между плоскостями (проводимость среды g равна нулю).
Полученные уравнения распадаются на две системы абсолютно независимые друг от друга, ибо в уравнения (1.2) входят неизвестные 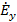 , , 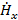 , ,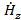 , а в уравнения (1.3) - неизвестные , а в уравнения (1.3) - неизвестные 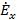 , , 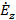 , , 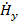 . Так как по условию задачи электромагнитные волны распространяются вдоль оси z, то система (1.2) определяет поля поперечно-электрические (H-волны), а система (1.3) - поля поперечно-магнитные (E-волны). Действительно, в поле (1.2) проекция вектора . Так как по условию задачи электромагнитные волны распространяются вдоль оси z, то система (1.2) определяет поля поперечно-электрические (H-волны), а система (1.3) - поля поперечно-магнитные (E-волны). Действительно, в поле (1.2) проекция вектора 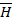 на направление распространения не равна нулю (проекция на направление распространения не равна нулю (проекция 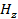 ), а вектор ), а вектор 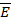 лежит в плоскости, перпендикулярной оси z. Аналогично в поле (1.3) проекция вектора лежит в плоскости, перпендикулярной оси z. Аналогично в поле (1.3) проекция вектора 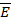 на направление распространения не равна нулю, а в плоскости, перпендикулярной оси z, лежит вектор на направление распространения не равна нулю, а в плоскости, перпендикулярной оси z, лежит вектор 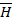 . .
Рассмотрим эти типы полей по отдельности.
2. Поперечно-магнитные поля
Выразим величины 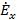 и и 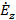 из первого и второго уравнения системы (1.3) через из первого и второго уравнения системы (1.3) через 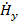 : :
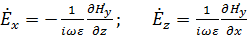 (1.4) (1.4)
Подставив их значения в последнее уравнение системы, получим дифференциальное уравнение для составляющей 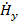 : :
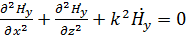 (1.5) (1.5)
Где 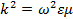 . .
Следовательно, расчет поперечно-магнитного поля в направляющей системе сводится к решению уравнения (1.5) при граничных условиях (1.1). Последние в рассматриваемом случае принимают вид
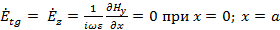 (1.6) (1.6)
или просто 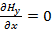 при при 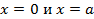 . .
Решение уравнения (1.5) будем искать методом разделения переменных, полагая, что
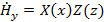 (1.7) (1.7)
Тогда уравнение (1.5) нетрудно привести к виду
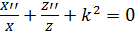 (1.8) (1.8)
Последнее уравнение эквивалентно двум уравнениям:
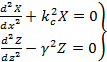 (1.9) (1.9)
где 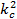 - неизвестная постоянная разделения, а - неизвестная постоянная разделения, а
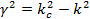 (1.10) (1.10)
Решение первого уравнения (1.9) целесообразно записать таким образом:
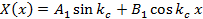 . .
Для второго уравнения (1.9) решение удобно представить в виде линейной комбинации показательных функций:
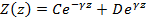 . .
Следовательно,
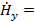 ( (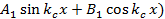 ( (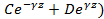 . (1.11) . (1.11)
Чтобы найти входящие в (1.11) неизвестные коэффициенты и постоянную разделения 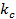 , используем граничные условия (1.6) . Поставив туда значение , используем граничные условия (1.6) . Поставив туда значение 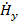 будем иметь будем иметь
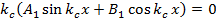 (1.12) (1.12)
при 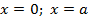
Условия (1.12), очевидно, могут быть удовлетворены, если положить 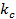 = 0. В этом случае проекция = 0. В этом случае проекция 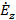 , как видно из (1.4), обращается в нуль не только на проводящих плоскостях, но и во всех точках пространства между ними. Тогда из (1.10) следует, что , как видно из (1.4), обращается в нуль не только на проводящих плоскостях, но и во всех точках пространства между ними. Тогда из (1.10) следует, что 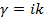 (величина (величина 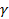 , как известно, носит название постоянной распространения). , как известно, носит название постоянной распространения).
Подставляя найденные значения 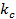 и и 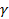 в выражения (1.11) и (1.4), получим: в выражения (1.11) и (1.4), получим:
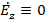
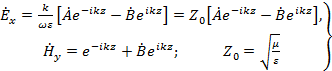 (1.13) (1.13)
Здесь мы положили, что 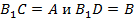 . .
Таким образом, решение системы уравнений (1.3) при 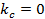 определяет электромагнитное поле в виде суммы двух бегущих волн, распространяющихся по оси z в противоположных направлениях. определяет электромагнитное поле в виде суммы двух бегущих волн, распространяющихся по оси z в противоположных направлениях.
Если полагать, что источник электромагнитной энергии находится где-то в точках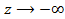 , то в линии, естественно, будет существовать только одна волна, распространяющаяся в направлении от , то в линии, естественно, будет существовать только одна волна, распространяющаяся в направлении от 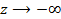 к к 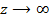 . В этом случае выражения для компонент электромагнитного поля принимают вид: . В этом случае выражения для компонент электромагнитного поля принимают вид:
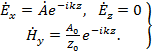 (1.14) (1.14)
Из равенств (1.14) вытекает, что векторы электромагнитного поля полученной волны не имеют составляющих на направление распространения. Следовательно, электромагнитное поле, определяемое уравнениями (1.4), (1.5), при 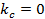 вырождается в волну поперечно-электромагнитного типа. вырождается в волну поперечно-электромагнитного типа.
Фазовая скорость волны (1.14) совпадает со скоростью распространения плоской волны в свободном пространстве с параметрами среды 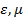 : :
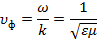
Для характеристики направляющей системы целесообразно ввести величину, называемую характеристическим сопротивлением
. Последнее определяется как отношение поперечной проекции вектора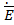 к перпендикулярной ей поперечной проекции вектора к перпендикулярной ей поперечной проекции вектора 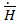 . .
В нашем случае характеристическое сопротивление 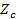 будет равно будет равно
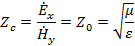
т.е. оно совпадает с волновым сопротивлением среды для плоской волны. Такое совпадение нельзя считать случайным, ибо волна ТЕМ в рассматриваемой системе аналогична по своей структуре плоской волне в неограниченном пространстве. Действительно, если в поле плоской волны, распространяющейся в неограниченном пространстве, внести две бесконечно-тонкие проводящие плоскости, перпендикулярные вектору 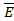 , то граничные условия (1.1) автоматически оказываются выполненными. , то граничные условия (1.1) автоматически оказываются выполненными.
Электромагнитное поле (1.14) в пространстве между проводящими плоскостями имеет волновой характер при любом значении частоты колебаний. Иными словами, поперечная волна в направляющей системе может существовать при любой частоте колебаний поля, причем распространение этой волны происходит со скоростью, зависящей лишь от параметров среды.
Полученное выше решение уравнений (1.3) оказывается не единственно возможным. В самом деле, условиям (1.6), (1.12) можно также удовлетворить если 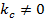 , но , но
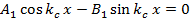 при при 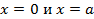
Легко убедиться, что левая часть последнего равенства будет обращаться в нуль при 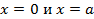 , если , если
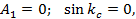
откуда вытекает, что
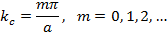
Постоянная распространения 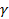 , которую в дальнейшем целесообразно обозначить , которую в дальнейшем целесообразно обозначить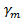 , согласно (1.10) будет равна , согласно (1.10) будет равна
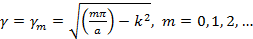 (1.15) (1.15)
Подставив найденное значение 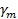 в выражение (1.12) и учитывая, что в выражение (1.12) и учитывая, что 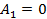 , получим , получим
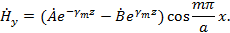
Аналогично ранее исследованному случаю поперечной волны мы можем положить 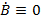 . Тогда, в соответствии с (1.5), выражения для проекций векторов поля будут иметь вид: . Тогда, в соответствии с (1.5), выражения для проекций векторов поля будут иметь вид:
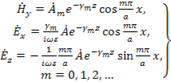 (1.16) (1.16)
Здесь коэффициент 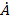 мы заменили на мы заменили на 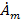 . .
Так как 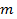 по определению - любое целое число, то в пространстве между параллельными проводящими плоскостями, помимо ранее найденной волны ТЕМ, может существовать бесчисленное множество полей поперечно-магнитного типа, характеризуемых различными значениями по определению - любое целое число, то в пространстве между параллельными проводящими плоскостями, помимо ранее найденной волны ТЕМ, может существовать бесчисленное множество полей поперечно-магнитного типа, характеризуемых различными значениями 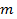 (поля (поля 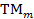 ). ).

Рис. 2 - Зависимость составляющей 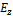 от координаты x в пространстве между проводящими плоскостями при различных значениях от координаты x в пространстве между проводящими плоскостями при различных значениях 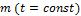
Из выражений (1.16) следует, что распределение поля вдоль оси х имеет форму стоячей волны. Характер изменения поля на интервале 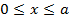 определяется числом (индексом) определяется числом (индексом) 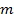 . Согласно (1.16) при различных . Согласно (1.16) при различных 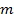 на промежутке между плоскостями будет укладываться различное число «полуволн» поля, причем это число как раз и равно на промежутке между плоскостями будет укладываться различное число «полуволн» поля, причем это число как раз и равно 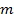 . На рис. 1.2 изображены кривые изменения . На рис. 1.2 изображены кривые изменения 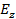 вдоль оси х, соответствующие разным вдоль оси х, соответствующие разным 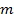 . (Максимальные значения . (Максимальные значения 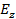 для различных «гармоник» здесь выбраны произвольно. Начальные фазы взяты или одинаковыми или отличающимися одна от другой на для различных «гармоник» здесь выбраны произвольно. Начальные фазы взяты или одинаковыми или отличающимися одна от другой на 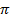 ) )
Нетрудно убедиться, что компоненты электромагнитного поля (1.16) при 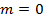 совпадают с компонентами поля (1.14), ибо совпадают с компонентами поля (1.14), ибо 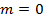 соответствует соответствует 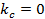 . Следовательно, поперечно-электромагнитную волну в пространстве между параллельными проводящими плоскостями можно рассматривать как вырожденный случай поля поперечно-магнитного типа. . Следовательно, поперечно-электромагнитную волну в пространстве между параллельными проводящими плоскостями можно рассматривать как вырожденный случай поля поперечно-магнитного типа.
Рассмотрим теперь формулу (1.15), определяющую постоянную распространения 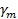 . .
Легко заметить, что при 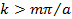 , , 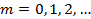 , постоянная распространения становится чисто мнимой величиной: , постоянная распространения становится чисто мнимой величиной:
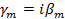 , ,
где
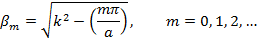
В этом случае поперечно-магнитное поле (1.16) будет иметь волновой характер, ибо выражения (1.16) при 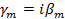 , представляют волны, распространяющиеся с определенной скоростью вдоль оси z. , представляют волны, распространяющиеся с определенной скоростью вдоль оси z.
Предположим, что при данных значениях частоты f, расстояния 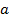 и заданном типе поля, характеризуемом величиной и заданном типе поля, характеризуемом величиной 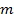 , выполняется соотношение , выполняется соотношение
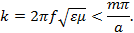
В этом случае электромагнитное поле (1.16) уже не будет иметь волнового характера, так как теперь 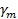 является величиной вещественной, и множитель является величиной вещественной, и множитель 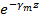 определяет лишь экспоненциальный характер убывания амплитуды колебаний поля в различных точках оси z. Электромагнитные поля такого типа обычно называют затухающими полями
(не смешивать с бегущими волнами, амплитуды которых экспоненциально затухают вдоль направления распространения). определяет лишь экспоненциальный характер убывания амплитуды колебаний поля в различных точках оси z. Электромагнитные поля такого типа обычно называют затухающими полями
(не смешивать с бегущими волнами, амплитуды которых экспоненциально затухают вдоль направления распространения).
Для любого значения 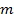 и и 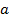 можно, очевидно, найти такую частоту колебаний, при которой постоянная распространения обращается в нуль. Из выражения (1.15) следует, что можно, очевидно, найти такую частоту колебаний, при которой постоянная распространения обращается в нуль. Из выражения (1.15) следует, что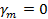 , если , если
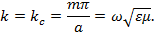
Частота колебаний электромагнитного поля, определенная из последнего равенства, имеет название критической частоты
и обозначается 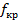 . Нетрудно видеть, что . Нетрудно видеть, что
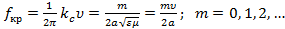 (1.17) (1.17)
Для каждой критической частоты можно рассчитать соответствующую ей критическую длину волны
:
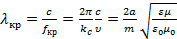 ; ; 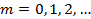 (1.18) (1.18)
Если 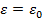 и и 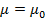 , то , то 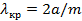 . .
Используя выражения (1.15), (1.17) и (1.18), получим
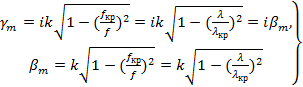 (1.19) (1.19)
Следовательно, при данных 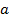 , , 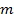 и и 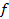 поперечно-магнитное поле поперечно-магнитное поле 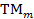 будет иметь форму бегущей волны в том случае, когда частота колебаний поля больше критической частоты (1.17), т. е. когда длина волны будет иметь форму бегущей волны в том случае, когда частота колебаний поля больше критической частоты (1.17), т. е. когда длина волны 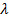 короче критической длины волны короче критической длины волны 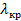 . Например ,поле . Например ,поле 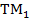 в линии с в линии с 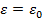 и и 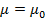 будет иметь волновой характер, если частота будет иметь волновой характер, если частота 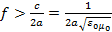 , или соответственно длина волны , или соответственно длина волны 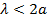 . .
Если же частота колебаний меньше критической частоты, поле становится затухающим.
Анализируя выражения (1.16) можно показать, что перенос электромагнитной энергии вдоль направляющей системы осуществляется только бегущими волнами. В самом деле, среднее значение проекции вектора Пойнтинга на ось z в рассматриваемом случае имеет вид

Если постоянная распределения 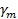 - величина чисто мнимая, то - величина чисто мнимая, то

При вещественном 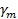 (затухающее поле) (затухающее поле)

Следовательно, мощность, заключенная в затухающем электромагнитном поле, является чисто колебательной. Последний вывод становится очевидным, если учесть, что проекция  в случае вещественной в случае вещественной 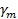 сдвинута по фазе относительно проекции сдвинута по фазе относительно проекции  на угол – на угол –  . .
Найдем фазовую скорость волны 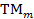 . Так как по определению . Так как по определению  , то, учитывая (1.17) - (1.18), получим , то, учитывая (1.17) - (1.18), получим
 , (1.20) , (1.20)
где  . .
Отсюда вытекает, что фазовая скорость волны 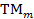 при при  больше скорости v
. При больше скорости v
. При  величина величина  становится бесконечно большой. становится бесконечно большой.
Характеристическое сопротивление
 (1.21) (1.21)
в случае поперечно-магнитных волн оказывается меньше характеристического сопротивления  . .
Таким образом, величины, характеризующие волны TM в рассматриваемой системе, зависят и от частоты колебаний 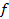 и от расстояния а
между направляющими плоскостями. Что же касается волны ТЕМ, то ее характеристики не зависят ни от и от расстояния а
между направляющими плоскостями. Что же касается волны ТЕМ, то ее характеристики не зависят ни от 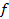 , ни от , ни от 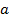 . Получается, что направляющая система как бы не оказывает влияния на распространение этой волны. . Получается, что направляющая система как бы не оказывает влияния на распространение этой волны.

Рис. 3 - Силовые линии векторов  и и  волны ТЕМ в пространстве между проводящими плоскостями волны ТЕМ в пространстве между проводящими плоскостями
Пользуясь выражениями (1.16), можно изобразить силовые линии электромагнитного поля различных типов волн. На рис. 3 показаны силовые линии волны ТЕМ в различных координатных плоскостях (сплошные линии соответствуют электрическому полю, пунктирные - магнитному). На рис. 4 приведены силовые линии волны 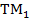 . .

Рис. 4 - Силовые линии векторов  и и  волны волны  в пространстве между проводящими плоскостями в пространстве между проводящими плоскостями
3. Поперечно-электрические поля
Выразим величины 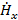 и и  из первого и второго уравнений системы (1.2) через из первого и второго уравнений системы (1.2) через 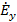 : :

Подставив найденные значения 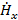 и и  в третье уравнение, получим для проекции в третье уравнение, получим для проекции 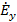 : :
 (1.22) (1.22)
Используя метод разделения переменных, легко показать, что решение уравнения (1.22) имеет вид:
 ( (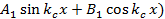 ( (

Аналогично предыдущему случаю будем рассматривать лишь волны, бегущие в положительном направлении оси z. Тогда  и и
 (1.23) (1.23)
где

Чтобы найти неизвестные, входящие в (1.23), воспользуемся граничными условиями:
 при при  и и  (1.24) (1.24)
Эти условия будут удовлетворены, если
 и и 
откуда следует:
 
Стало быть, выражения для проекций векторов поля поперечно-электрического типа будут иметь вид:
 (1.25) (1.25)
Из выражений (1.25) вытекает, что в пространстве между параллельными проводящими плоскостями может существовать бесчисленное множество поперечно-электрических полей, соответствующих различным значениям 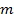 (поля (поля  ). Число ). Число 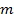 здесь имеет тот же смысл, что и в случае полей поперечно-магнитного типа. Однако в отличие от предыдущего случая поле здесь имеет тот же смысл, что и в случае полей поперечно-магнитного типа. Однако в отличие от предыдущего случая поле  в направляющей системе не существует, ибо при в направляющей системе не существует, ибо при  все составляющие векторов все составляющие векторов 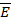 и и 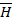 обращаются в нуль. обращаются в нуль.
Электромагнитное поле (1.25) будет иметь волновой характер, если
 (1.26) (1.26)
есть мнимое число. Это выполняется при условии, что величина  . Следовательно, для каждого типа поперечно-электрического поля можно определить критическую частоту . Следовательно, для каждого типа поперечно-электрического поля можно определить критическую частоту  , при которой , при которой

Эта частота равна
 (1.27) (1.27)
Соответственно, критическая длина волны
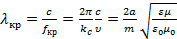 ; (1.28) ; (1.28)
Подставив найденные значения 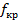 и и  в выражение (1.26), получим в выражение (1.26), получим

Стало быть, поперечно-электрическое поле имеет волновой характер, если  . При . При  поле (1.25) будет затухать вдоль оси z. Затухающее поле ТЕ, так же как и TM, характеризуется реактивной мощностью, т. е. оно в переносе энергии вдоль направления распространения не участвует поле (1.25) будет затухать вдоль оси z. Затухающее поле ТЕ, так же как и TM, характеризуется реактивной мощностью, т. е. оно в переносе энергии вдоль направления распространения не участвует
Фазовая скорость поперечно-электрической волны определяется выражением
 (1.29) (1.29)
откуда следует, что при  она больше скорости она больше скорости  . .
Характеристическое сопротивление волны в направляющей системе равно
 (1.30) (1.30)
Эта величина оказывается больше характеристического сопротивления  среды, заполняющей пространство между проводниками. среды, заполняющей пространство между проводниками.
Таковы свойства поперечно-электрических волн в пространстве между параллельными проводящими плоскостями.
На рис. 5 изображены силовые линии электромагнитного поля волны  . .

Рис. 5 - Силовые линии векторов  и и  волны волны  в пространстве между проводящими плоскостями в пространстве между проводящими плоскостями
4. Скорости распространения электромагнитных волн
Пусть электромагнитная волна распространяется в среде (или направляющей системе) без потерь. В режиме установившихся гармонических колебаний мгновенные комплексные значения любой из проекций вектора  или или  на оси прямоугольной системы координат имеют вид: на оси прямоугольной системы координат имеют вид:
 (1.31) (1.31)
Здесь ось z принята за направление распространения волны.
Из выражения (1.31) следует, что изменение фазы поля вдоль направления распространения определяется величиной  . Отсюда мы находим фазовую скорость волны . Отсюда мы находим фазовую скорость волны
 (1.32) (1.32)
как скорость движения поверхности равных фаз вдоль оси z. Таким образом, фазовая скорость характеризует изменение начальных фаз гармонических колебаний по направлению движения волны.
Рассмотрим теперь более сложный вопрос о распространении колебаний произвольной формы. В дальнейшем такие колебания мы будем условно называть сигналами.
Очевидно, у нас нет оснований утверждать, что скорость распространения сигнала будет совпадать с фазовой скоростью. В самом деле, последняя, как было установлено, характеризует лишь фазовые соотношения между гармоническими колебаниями в различных точках пространства, когда эти колебания уже возникли и установились всюду.
Предположим, что в точке 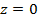 имеется сигнал, меняющийся во времени по закону имеется сигнал, меняющийся во времени по закону 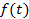 . Выясним, какой вид будет иметь этот сигнал в других точках оси z при t > 0; иными словами, определим функцию . Выясним, какой вид будет иметь этот сигнал в других точках оси z при t > 0; иными словами, определим функцию 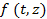 , если известна функция , если известна функция 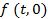 , а также известны характеристики среды, в которой происходит распространение. Используя интеграл Фурье, представим , а также известны характеристики среды, в которой происходит распространение. Используя интеграл Фурье, представим 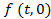 в виде: в виде:
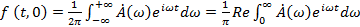 (1.33) (1.33)
где 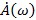 - спектральная плотность функции - спектральная плотность функции 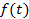 . Согласно выражению (1.33) функция . Согласно выражению (1.33) функция 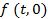 представляет собой сумму множества гармонических колебаний с частотами представляет собой сумму множества гармонических колебаний с частотами 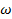 и амплитудами и амплитудами 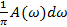 . Совокупность этих колебаний, как известно, образует спектр функции . Совокупность этих колебаний, как известно, образует спектр функции
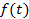 . .
Но каждой составляющей 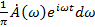 при распространении колебаний вдоль оси z соответствует волна при распространении колебаний вдоль оси z соответствует волна
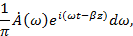
где 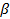 - волновое число. Поэтому функцию - волновое число. Поэтому функцию 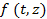 в любой точке оси z можно представить в виде в любой точке оси z можно представить в виде
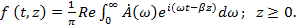 (1.34) (1.34)
Из формулы (1.34) следует, что распространение сигнала в данном направлении обусловлено движением всех его гармонических составляющих.
В общем случае фазовая скорость волны зависит от частоты колебаний (подробнее об этом см. ниже). При наличии такой зависимости различные гармонические составляющие сигнала будут двигаться вдоль оси z с различными фазовыми скоростями. А это, очевидно, может привести к тому, что форма сигнала по мере его распространения будет изменяться.
Так как волновое число 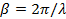 есть функция частоты, т. е. есть функция частоты, т. е. 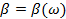 , в (1.34) вместо интегрирования по , в (1.34) вместо интегрирования по 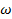 можно перейти к интегрированию по можно перейти к интегрированию по 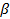 : :
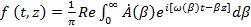 . (1.35) . (1.35)
Пусть действительный спектр сигнала ограничен частотами 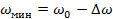 и и 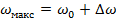 , и, кроме того, , и, кроме того, 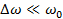 ( (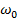 - средняя частота спектра). Тогда интегрирование в (1.34) будет происходить по промежутку - средняя частота спектра). Тогда интегрирование в (1.34) будет происходить по промежутку 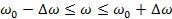 , а в (1.35) - по промежутку , а в (1.35) - по промежутку 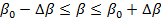 . Здесь . Здесь 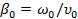 - среднее значение волнового множителя, соответствующее средней частоте - среднее значение волнового множителя, соответствующее средней частоте 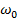 и фазовой скорости на этой частоте, а и фазовой скорости на этой частоте, а 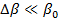 . На основании этого вместо (1.35) будем иметь . На основании этого вместо (1.35) будем иметь
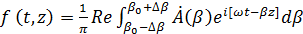 (1.36) (1.36)
Сигнал, определяемый интегралом (1.36), называется волновым пакетом
или группой волн
.
Рассматривая 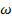 как функцию переменной как функцию переменной 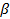 , разложим , разложим 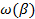 в ряд по степеням в ряд по степеням 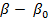 : :
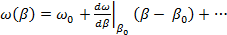 (1.37) (1.37)
и подставим 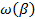 из (1.37) в (1.36). из (1.37) в (1.36).
При малом промежутке интегрирования в разложении (1.37) можно ограничиться двумя первыми членами. В этом случае интеграл (1.36) принимает вид:
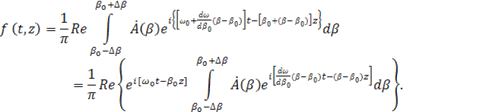
Здесь 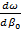 означает производную означает производную 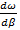 при при 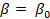 . .
Введя далее новую переменную интегрирования 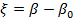 , получим , получим
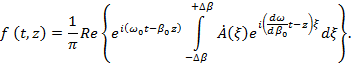
Будем полагать, что 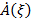 - непрерывная медленно меняющаяся функция. Тогда ее на малом интервале - непрерывная медленно меняющаяся функция. Тогда ее на малом интервале 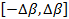 можно считать постоянной, равной можно считать постоянной, равной 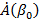 . В этом случае . В этом случае
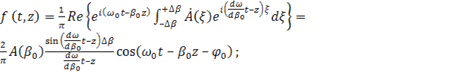 (1.38) (1.38)
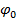 - аргумент комплексной величины - аргумент комплексной величины 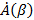 . .
Выражение (1.38), таким образом, определяет рассматриваемый сигнал в любой точке 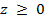 . Функция . Функция
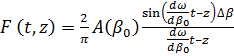 (1.39) (1.39)
вследствие того, что 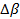 мало, является медленно меняющейся функцией переменных мало, является медленно меняющейся функцией переменных 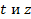 . Поэтому ее можно считать амплитудой волны . Поэтому ее можно считать амплитудой волны 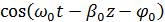 . При . При 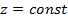 функция функция 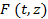 является огибающей сигнала является огибающей сигнала 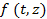 с узким (а точнее, с бесконечно узким) частотным спектром. с узким (а точнее, с бесконечно узким) частотным спектром.
Из формулы (1.39) видно, что с течением времени огибающая перемещается вдоль оси 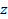 . О ее движении удобно судить по перемещению максимума, находящегося в точке . О ее движении удобно судить по перемещению максимума, находящегося в точке 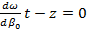 . .
Нетрудно сообразить, что с течением времени этот максимум движется вдоль оси 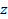 со скоростью со скоростью
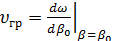 (1.40) (1.40)
Последняя получила наименование групповой скорости
. Она-то и определяет скорость распространения сигнала типа «волновой пакет».
Установим связь между групповой и фазовой скоростями. Дифференцируя выражение (1.32) по частоте, получим
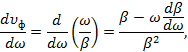
откуда
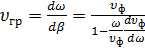 (1.41) (1.41)
Если фазовая скорость не зависит от частоты, т.е. 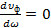 , то и , то и 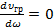 . В этом случае . В этом случае 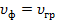 . .
Зависимость фазовой скорости от частоты колебаний в физике принято называть дисперсией
, а среду, в которой это явление наблюдается - дисперсной средой
.
Подобная зависимость характерна, например, для нашей направляющей системы. В самом деле, фазовая скорость волны ТЕ или TM, распространяющейся между проводящими плоскостями, равна
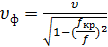 (1.42) (1.42)
а волновое число
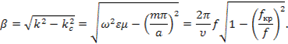
Используя соотношение (1.40) или (1.41), для групповой скорости получим
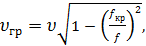 (1.43) (1.43)
и соответственно
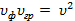 (10.44) (10.44)
На рисунке 6 показаны графики изменения фазовой и групповой скоростей (1.42), (1.44) в зависимости от частоты колебаний.

Рис. 6 - Зависимость фазовой и групповой скоростей волны, распространяющейся между параллельными плоскостями, от частоты колебаний
Заключение
Наиболее простой направляющей системой является совокупность двух параллельных проводящих бесконечных плоскостей, пространство между которыми заполнено диэлектриком. Конечно, направляющая система такого типа представляет лишь теоретический интерес. Тем не менее, анализ электромагнитного поля в ней позволяет выяснить основные особенности распространения электромагнитных волн в реальных направляющих устройствах.
Список использованной литературы
1. Гольдштейн Л.Д., Зернов Н.В. Электромагнитные поля и волны.
2. Семенов Н.А. Техническая электродинамика.
3. Бредов М.М., Румянцев В.В., Топтыгин И.Н. Классическая электродинамика.
|