 МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО РЫБОЛОВСТВУ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
 КафедраТМ КафедраТМ
Курсовая работа
По дисциплине: «Теоретическая механика»
«Исследование движения механической системы с использованием общих теорем и принципов динамики»
А-261(2)
Выполнил Проверил
Студент: Ларионов Д.С. Преподаватель: Каиров Т.В.
Дата: ____________ Дата: _____________
Подпись: _________ Подпись: __________
Оценка: ___________
Мурманск
2008
 Содержание Содержание
1.
Исследование движения механической системы с использованием общего уравнения динамики …………………………………………2
2.
Исследование движения механической системы с использованием общего уравнения динамики в обобщенных координатах (уравнение Лагранжа второго рода)………………………………………………..7
3.
Список использованной литературы…………………………………10
1.
Исследование движения механической системы с использованием общего уравнения динамики
Исходные данные
Д3
т1,
кг
|
т2,
кг
|
т3
,
кг
|
R1
,
м
|
R2
,
м
|
r2
,
м
|
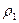 ,
,
м
|
Р,
Н
|
М,
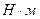
|
Мс
,
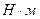
|
| 250
|
150
|
400
|
0,4
|
0,3
|
0,15
|
0,2
|
15000
|
6000
|
500
|
 Применим в ходе анализа движения механизма общее уравнение динамики. Применим в ходе анализа движения механизма общее уравнение динамики.
1.1 Зададим направления ускорений (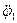 , , 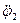 , , 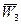 ) звеньев механизма. Предположим, что направления этих ускорений совпадают с положительным направлением координат ) звеньев механизма. Предположим, что направления этих ускорений совпадают с положительным направлением координат 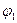 , , 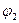 , , определяющих положение этих звеньев. Приложим к телам системы силовые факторы инерции. Силы инерции звеньев 1 и 2, вращающихся вокруг осей , , определяющих положение этих звеньев. Приложим к телам системы силовые факторы инерции. Силы инерции звеньев 1 и 2, вращающихся вокруг осей 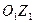 и и 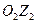 , соответственно приводятся к моментам сил инерции , соответственно приводятся к моментам сил инерции 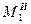 и и 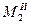 направленным противоположно соответствующим ускорениям направленным противоположно соответствующим ускорениям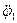 и и 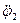 , величины которых равны: , величины которых равны:
 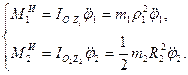
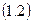 Сила инерции груза 3, движущегося поступательно с ускорением Сила инерции груза 3, движущегося поступательно с ускорением 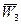 , направлена противоположно ускорению , направлена противоположно ускорению 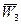 и численно равна и численно равна
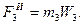
Учитывая, что взаимосвязь между ускорениями :

выражения (1.1) и (1.2) примут вид:
 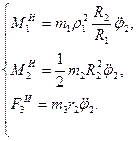
1.2Зададим механической системе возможное перемещение (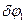 , , 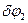 , , 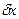 ) в направлении положительного отсчета соответствующих координат и составим общее уравнение динамики для этой системы, приравняв к нулю сумму элементарных работ всех внешних (заданных) сил и сил инерции материальных точек системы наэтом возможном перемещении: ) в направлении положительного отсчета соответствующих координат и составим общее уравнение динамики для этой системы, приравняв к нулю сумму элементарных работ всех внешних (заданных) сил и сил инерции материальных точек системы наэтом возможном перемещении:
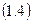 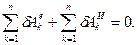
В нашем случае на механическую систему действуют силы тяжести 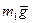 , , 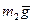 , , 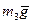 , вращающий момент , вращающий момент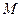 ,
момент сопротивления вращению ,
момент сопротивления вращению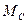 ,
силы реакции в опорах ,
силы реакции в опорах 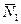 , , 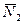 , , 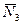 , , 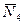 , и силы инерции , и силы инерции 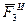 , , 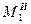 , , 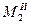 . Поскольку на систему наложены идеальные связи (шарниры без трения . Поскольку на систему наложены идеальные связи (шарниры без трения 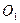 и и  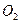 гибкая нерастяжимая нить, а также существует внутренняя связь между звеньями 1 и 2, которую можно представить либо как зубчатое зацепление без трения, либо как фрикционное зацепление без проскальзывания), то по определению элементарная работа сил реакций идеальной связи равна нулю и не входит в (1.4). Заметим сразу же, что равны нулю и не входят в (1.4) элементарные работы сил гибкая нерастяжимая нить, а также существует внутренняя связь между звеньями 1 и 2, которую можно представить либо как зубчатое зацепление без трения, либо как фрикционное зацепление без проскальзывания), то по определению элементарная работа сил реакций идеальной связи равна нулю и не входит в (1.4). Заметим сразу же, что равны нулю и не входят в (1.4) элементарные работы сил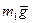 , , 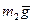 , , 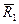 , , 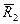 , , 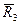 , , 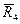 , таккак эти силы приложены к неподвижным точкам. Знак каждой работы устанавливается по общему правилу: если направление силового фактора (силы или момента) совпадает с направлением соответствующего ему перемещения (линейного или углового), то работа считается положительной, в противном случае работа силового фактора отрицательна. , таккак эти силы приложены к неподвижным точкам. Знак каждой работы устанавливается по общему правилу: если направление силового фактора (силы или момента) совпадает с направлением соответствующего ему перемещения (линейного или углового), то работа считается положительной, в противном случае работа силового фактора отрицательна.
Итак, общее уравнение динамики для нашей механической системы имеет вид:
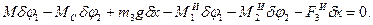
Приведем зависимости между координатами звеньев:
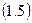 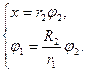
Так как на механическую систему наложены стационарные и голономные связи, то записать зависимости между возможными перемещениями звеньев можно аналогично (1.5):
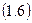 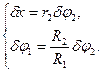
С учетом (1.6) выражение (1.5) примет вид:
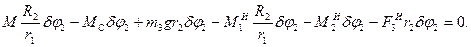
После сокращения на 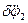 имеем имеем
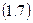 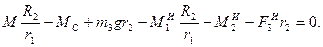
 Подставив в (1.7) вместо Подставив в (1.7) вместо 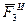 , , 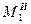 , , 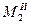 их выражения из (1.3), получим их выражения из (1.3), получим
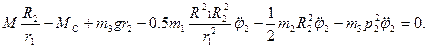
откуда
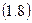 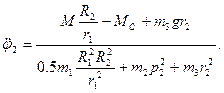
Подставив в (1.8) исходные данные, находим
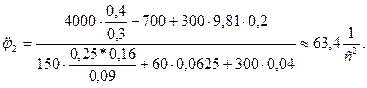
Определив угловое ускорение 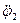 звена 2, найдем закон его движения: звена 2, найдем закон его движения:
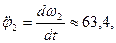
Проинтегрируем это равенство, учитывая, что для начала движения 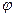 20
= 0 и 20
= 0 и 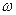 20
= 0: 20
= 0:
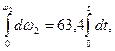
Откуда 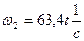 . .
Учитывая, что 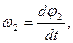 и выполнив аналогичные преобразования, получим и выполнив аналогичные преобразования, получим
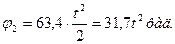
 1.3. Исследовательская часть 1.3. Исследовательская часть
Для определения натяжения нити, на которой подвешен груз 3, и окружного усилия в точке касания звеньев 1 и 2 составим общее уравнение динамики для звена 1 и отдельно для груза 3. При этом искомые усилия становятся внешними силами по отношению к этим телам. Для звена 2 общее уравнение динамики примет вид
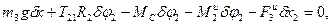
Откуда
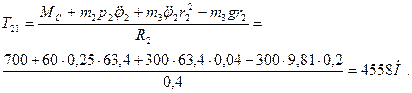
Для груза 3 общее уравнение динамики примет вид
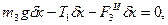
откуда, учитывая, что 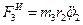 , имеем , имеем
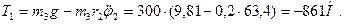
2.
Исследование движения механической системы с использованием общего уравнения динамики в обобщенных координатах (уравнение Лагранжа второго рода)
Исходные данные
Д4
кг
|
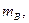
кг
|
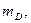
кг
|
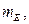
кг
|
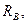
м
|
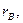
м
|
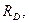
м
|
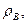
м
|
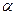
|
f
|
S,
м
|
| 3000 |
2000 |
400 |
300 |
0,5 |
0,3 |
0,4 |
0,2 |
60◦
|
0,11 |
6 |
 Рассмотрим движение неизменяемой системы с идеальными связями, движущимися под воздействием внешних сил: Рассмотрим движение неизменяемой системы с идеальными связями, движущимися под воздействием внешних сил:
· тяжести 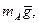 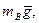 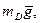 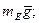
· трения скольжения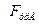
Реакции идеальных связей не учитываем, так как их элементарная работа равна 0.
Применим для анализа движения рассматриваемой механической системы на заданном перемещении S уравнение Лагранжа второго рода:
 (2.1)
(2.1)
Где –Т- кинетическая энергия системы за время движения;
q- обобщенная координата системы (q=x);
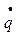 -
обобщенная скорость системы ( -
обобщенная скорость системы (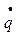 = =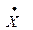 = =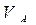 )
; )
;
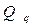 -
обобщенная сила системы, соответствующая обобщенной координате. С учетом принятых обозначений (2.1) примет вид: -
обобщенная сила системы, соответствующая обобщенной координате. С учетом принятых обозначений (2.1) примет вид:
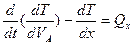 (2.2)
(2.2)
Кинетическая энергия механической системы была найдена в РГЗ №1:
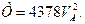 (2.3)
(2.3)
Найдем сумму элементарных работ всех действующих на систему внешних сил бесконечно малом перемещении тела А
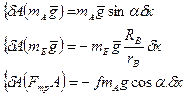
Сумму элементарных работ всех внешних сил найдем по формуле:
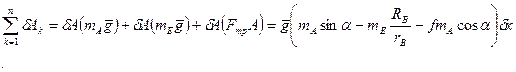 (2.4) (2.4)
По определению, обобщенная сила, соответствующая обобщенной координате х, равна:
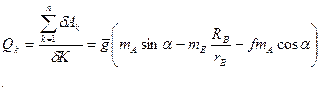 (2.5) (2.5)
Вычислим производные уравнения (2.2):
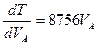 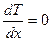 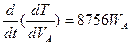 (2.6) (2.6)
Подставляя (2.5) и (2.6) в (2.2) имеем:
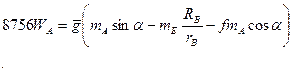
Определим скорость тела А:
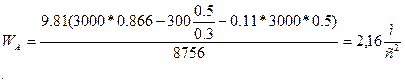
Умножив последнее равенство на 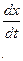 , получим: , получим:
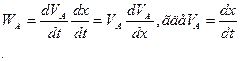
 Выше было указано, что Выше было указано, что
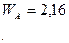 , поэтому: , поэтому:
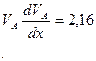
Проинтегрировав данное равенство и учитывая, что x=S, получим:
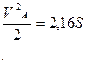
откуда :
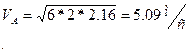
Список использованной литературы:
1. Айзерман Т. Б. и др. Руководство к решению задач по теоретической механике. – М.: Высш. шк., 1985. – 367 с.
2. Бать И. и др. Теоретическая механика в примерах и задачах. – М.: Высш. шк., 1990. – 631 с.
3. Тарг С.М. Краткий курс теоретической механики : Учеб. Для втузов. – 10-е изд., перераб. и доп. – М.: Высш. шк., 1986. – 416 с.
|