Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Контрольная работа
По дисциплине: Физика
Новосибирск, 2009
Вариант 3
703. Светильник в виде цилиндра из молочного стекла имеет размеры: длину 25 см, диаметр 24 мм. На расстоянии 2 м при нормальном падении лучей возникает освещенность 15 лк. Определить силу света; яркость и светимость его, считая, что указанный излучатель косинусный.
Решение: Источники, яркость которых одинакова по всем направлениям, называются ламбертовскими или косинусными. Величина светового потока 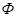 равна равна
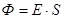
Где 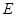 – освещенность на поверхности – освещенность на поверхности
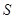 – площадь поверхности, для сферы – площадь поверхности, для сферы 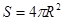
Для изотропного источника сила света 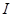 равна равна
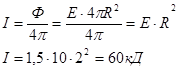
Светимость объекта – отношение светового потока, испускаемого источником к площади поверхности источника освещения. Для упрощения пренебрежением излучением, испускаемых с торца цилиндра.
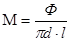
где 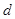 – диаметр светящегося цилиндра – диаметр светящегося цилиндра
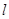 – длина светящегося цилиндра – длина светящегося цилиндра
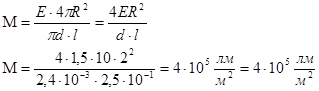
Для косинусного источника света светимость и яркость объекта связаны соотношением:
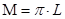 , где , где 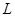 – яркость объекта – яркость объекта
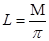
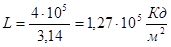
Ответ: Сила света 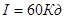
Светимость 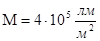
Яркость 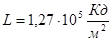
713. Температура абсолютно черного тела Т = 2 кК. Определить длину волны λm
, на которую приходится максимум испускательной способности и спектральную плотность энергетической светимости (rλ,
)max
для этой длины волны.
Решение: По закону Вина
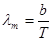 (1) (1)
где 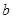 – константа – константа 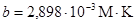
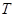 – температура тела, – температура тела, 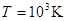
Этот закон связывает длину волны максимума испускательной способности с температурой тела.
Плотность энергетической светимости 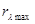 определим из формулы Планка: определим из формулы Планка:
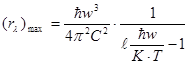 (2) (2)
где 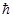 – постоянная Планка, – постоянная Планка, 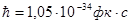
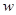 – циклическая частота света, связанная с длиной волны сооношением: – циклическая частота света, связанная с длиной волны сооношением:
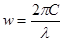 (3) (3)
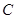 - скорость света, - скорость света, 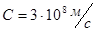
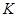 - постоянная Больцмана, - постоянная Больцмана, 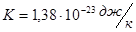
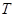 - температура абсолютно черного тела. - температура абсолютно черного тела.
Подставим (3) в (2) получим:
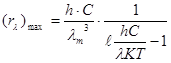
где 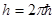 – постоянная Планка, – постоянная Планка, 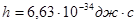
Определим по закону Вина длину волны 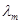
Найдем спектральную плотность энергетической светимости
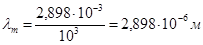 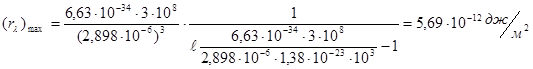
Размерность 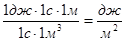
Ответ:
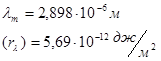
723. Фотон с энергией ε = 10 эВ падает на серебряную пластину и вызывает фотоэффект. Определить импульс р, полученный пластиной, если принять, что направления движения фотона и фотоэлектрона лежат на одной прямой, перпендикулярной поверхности пластин.
Решение: Формула Эйнштейна для фотоэффекта
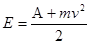 (1) (1)
Где 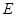 - энергия падающего фотона - энергия падающего фотона
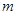 – масса фотоэлектрона, – масса фотоэлектрона, 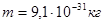
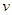 – скорость фотоэлектрона – скорость фотоэлектрона
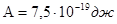
Импульс фотона 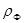 равен: равен:
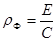 (2) (2)
где 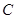 – скорость света, – скорость света, 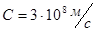
Таким образом, из закона сохранения импульса, импульс 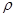 , полученный пластиной, равен: , полученный пластиной, равен:
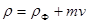
Скорость вылета фотоэлектрона из пластины из уравнения (1) равна
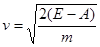
Откуда, импульс пластины 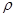 равен: равен:
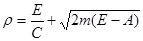
Размерность
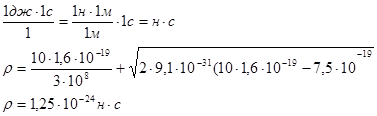
Ответ: импульс пластины 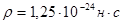
733. Определить постоянную Планке h, если известно, что фотоэлектроны, вырываемые с поверхности металла светом с частотой 2,2ּ 1011
с-1
, полностью задерживаются обратным потенциалом 6,6 В, а вырываемые светом с частотой 4,6ּ 1011
c-1
– потенциалом 16,5 В.
Решение: Формула Эйнштейна для фотоэффекта
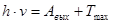 (1) (1)
где 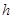 – постоянная Планка (необходимо найти) – постоянная Планка (необходимо найти)
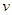 - частота падающего света - частота падающего света
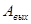 - работа выхода фотоэлектрона - работа выхода фотоэлектрона
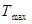 – кинетическая энергия, с которой фотоэлектрон выходит с поверхности. – кинетическая энергия, с которой фотоэлектрон выходит с поверхности.
Под действием приложенного поля кинетическая энергия фотоэлектрона переходит в потенциальную энергию электрона в электрическом поле, тогда
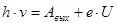 (2) (2)
где 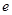 – заряд фотоэлектрона, – заряд фотоэлектрона, 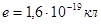
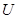 - величина задерживающего потенциала - величина задерживающего потенциала
Тогда из уравнения (2) следует:

Размерность
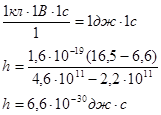
Ответ: постоянная Планка 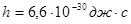
743. Какая доля энергии фотона приходится при эффекте Комптона на электрон отдачи, если рассеяние фотона происходит на угол θ=π/2 рад? Энергия фотона до рассеяния ε = 0,51 МэВ.
Решение: Запишем формулу Комптона:
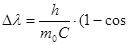  ) (1) ) (1)
где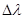 – изменение длины волны фотона – изменение длины волны фотона
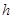 – постоянная Планка, – постоянная Планка, 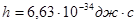
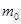 - масса электрона, - масса электрона, 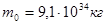
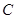 - скорость света, - скорость света, 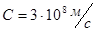
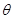 – угол между фотоном и электроном после столкновения – угол между фотоном и электроном после столкновения
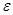 – энергия фотона до столкновения – энергия фотона до столкновения
 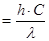 (2) (2)
где 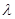 – первоначальная длина волны – первоначальная длина волны
Энергия фотона ε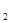 после столкновения: после столкновения:
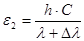 (3) (3)
Из закона сохранения энергии, энергия, переданная электрону, равна:
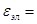  - -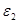 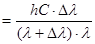 (4) (4)
И доля энергии 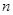 , переданная электрону, равна: , переданная электрону, равна:
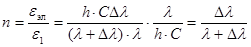 (5) (5)
С учетом выражения (2) получаем:
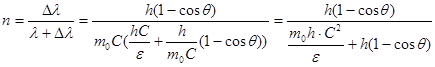
Подставим значение (учитывая, что 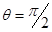 ) )
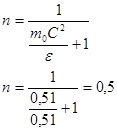
Мы использовали тот факт, что энергия покоя электрона 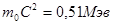
Ответ: доля энергии фотона, затраченная на электрон отдачи 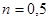
753. Определить коэффициент отражения поверхности, если при энергетической освещенности Ее
= 120 Вт/м2
давление р
света на нее оказалось равным 0,5 мкПа.
Решение: Давление света при нормальном падении на поверхность
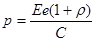
где 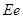 – энергетическая освещенность – энергетическая освещенность
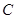 - скорость света, - скорость света, 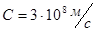
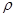 - коэффициент отражения - коэффициент отражения
Откуда получаем:
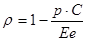
Подставим значения:
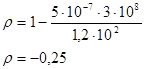
Ответ: коэффициент отражения 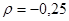
803. Вычислить по теории Бора период Т
вращения электрона в атоме водорода, находящегося в возбужденном состоянии, определяемом главным квантовым числом n = 2.
Решение: Период обращения электрона в модели атома по Бору:
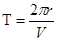 (1) (1)
где 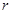 – радиус орбиты – радиус орбиты
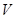 – скорость движения электрона по орбите – скорость движения электрона по орбите
Условие для стационарных орбит:
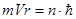
где 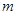 – масса электрона, – масса электрона,
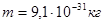 (2) (2)
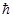 - постоянная Планка, - постоянная Планка, 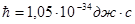
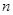 - главное квантовое число - главное квантовое число
Ньютоновское уравнение движения по орбите:
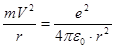 (3) (3)
где 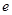 - заряд электрона, - заряд электрона, 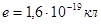
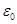 – электрическая постоянная, – электрическая постоянная, 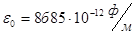
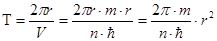
Получим из (2) и (3) выражение для радиуса орбит:
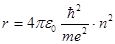
Откуда выражение для периода вращения:
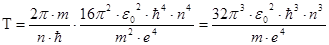
Размерность 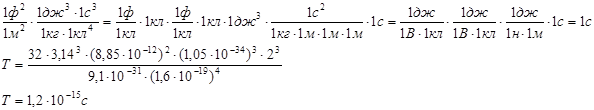
Ответ: период обращения 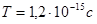
823. Какова должна быть кинетическая энергия Т
протона в моноэнергетическом пучке, используемого для исследования структуры с линейными размерами l
≈10-13
см?
Решение: Соотношение неопределенностей для координат и импульса:
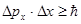 (1) (1)
где 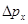 – неопределенность проекции импульса на ось ОХ – неопределенность проекции импульса на ось ОХ
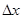 – неопределенность координаты – неопределенность координаты
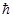 – постоянная Планка, – постоянная Планка, 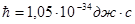
Таким образом, для неопределенности импульса
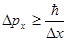 (2) (2)
Импульс частицы связан с кинетической энергией 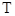
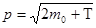 (3) (3)
где 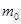 – масса покоя протона, – масса покоя протона, 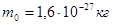
Подставим (3) в (2), получим:
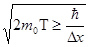
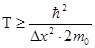
Размерность 
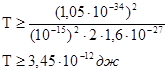
или 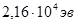
Ответ: кинетическая энергия должна быть больше 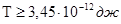
|