Федеральное агентство по образованию Российской Федерации
Государственное образовательное учреждение высшего профессионального образования Южно-Уральский государственный университет.
Факультет Коммерции
Кафедра «Товароведение и экспертиза потребительских товаров»
«Кривые второго порядка: эллипс, окружность, парабола, гипербола»
РЕФЕРАТ
По дисциплине Высшая математика.
Проверила
Пермина Александра Николаевна
Автор работы
студент группы 131
Кравченко Ольга Владимировна
Реферат защищен
с оценкой________________
Челябинск 2009
Кривые второго порядка: эллипс, окружность, парабола, гипербола.
Кривыми второго порядка
на плоскости называются линии пересечения кругового конуса с плоскостями, не проходящими через его вершину.
Если такая плоскость пересекает все образующие одной полости конуса, то в сечении получается эллипс
, при пересечении образующих обеих полостей – гипербола
, а если секущая плоскость параллельна какой-либо образующей, то сечением конуса является парабола
.
Кривая второго порядка
на плоскости в прямоугольной системе координат описывается уравнением: 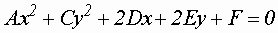
Эллипс.
Множество всех точек на плоскости, для которых сумма расстояний до двух фиксированных точек F 1
и F 2
есть заданная постоянная величина, называется эллипсом
.

Каноническое уравнение эллипса.
Для любого эллипса можно найти декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
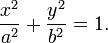 ,где ,где 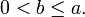
Оно описывает эллипс с центром в начале координат, оси которого совпадают с осями координат. Число a
называют большой полуосью эллипса
, а число b
– его малой полуосью
.
Свойства эллипса:
- Фокальное свойство.
Если F
1
и F
2
— фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой ( F
1
X
) равен углу между этой касательной и прямой ( F
2
X
) .
- Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса. Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
- Эволютой эллипса является астроида.
- Эксцентриситетом
эллипса называется отношение
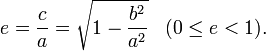 . Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут. . Эксцентриситет характеризует вытянутость эллипса. Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
Эллипс также можно описать как
- фигуру, которую можно получить из окружности, применяя аффинное преобразование
- ортогональную проекцию окружность на плоскость.
- Пересечение плоскости и кругового цилиндра.
Окружность.
 Окружность
— геометрическое место точек плоскости, равноудалённых от заданной точки, называемой её центром, на заданное ненулевое расстояние, называемое её радиусом. Окружность
— геометрическое место точек плоскости, равноудалённых от заданной точки, называемой её центром, на заданное ненулевое расстояние, называемое её радиусом.
Каноническое уравнение окружности.
Общее уравнение окружности записывается как:
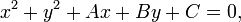
или

Точка 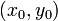 — центр окружности, R
— её радиус. — центр окружности, R
— её радиус.
Уравнение окружности радиуса R
с центром в начале координат:
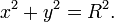
Свойства окружности:
- Прямая может не иметь с окружностью общих точек; иметь с окружностью одну общую точку (касательная); иметь с ней две общие точки (секущая).
- Касательная к окружности всегда перпендикулярна её диаметру, один из концов которого является точкой касания.
- Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
- Точка касания двух окружностей лежит на линии, соединяющей их центры.
- Длину окружности с радиусом R
можно вычислить по формуле C
= 2π R
.
- Вписанный угол либо равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180°.
- Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
- Вписанный угол, опирающийся на дугу длиной в половину окружности равен 90°.
- Угол между двумя секущими, проведенными из точки, лежащей вне окружности равен полуразности мер дуг, лежащих между секущими.
- Угол между пересекающимися хордами равен полусумме мер дуги лежащей в угле и дуги напротив нее.
- Угол между касательной и хордой равен половине дуги, стягиваемой хордой.
- Отрезки касательных к окружности, проведённых из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
- При пересечении двух хорд произведение отрезков, на которые делится одна из них точкой пересечения, равно произведению отрезков другой.
- Произведение длин расстояний от выбранной точки до двух точек пересечения окружности и секущей проходящей через выбранную точку не зависит от выбора секущей и равно абсолютной величине степени точки относительно окружности.
Квадрат длины отрезка касательной равен произведению длин отрезков секущей и равен абсолютной величине степени точки относительно окружности.
- Окружность является простой плоской кривой второго порядка.
- Окружность является коническим сечением и частным случаем эллипса.
Парабола.
Параболой
называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.
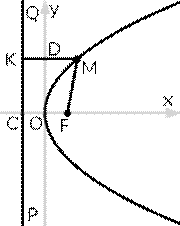 Каноническое уравнение
параболы в прямоугольной системе координат: Каноническое уравнение
параболы в прямоугольной системе координат:
 (или (или 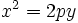 , если поменять местами оси) , если поменять местами оси)
где р
(фокальный параметр) - расстояние от фокуса до директрисы
Свойства параболы:
- Парабола — кривая второго порядка.
- Она имеет ось симметрии, называемой осью параболы
. Ось проходит через фокус и перпендикулярна директрисе.
- Пучок лучей параллельных оси, отражаясь в параболе, собирается в её фокусе. Для параболы с вершиной в начале координат (0; 0) и положительным направлением ветвей фокус находится в точке (0; 0,25).
- Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
- Парабола является антиподерой прямой.
- Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
- При вращении параболы вокруг оси симметрии получается эллиптический параболоид.
· Прямая пересекает параболу не более чем в двух точках.
· Эксцентриситет параболы е
=1.
Гипербола.
Геометрическое место точек плоскости, для которых разность расстояний до двух фиксированных точек есть величина постоянная, называют гиперболой
.
 Для любой гиперболы можно найти декартову систему координат такую, что гипербола будет описываться уравнением
: Для любой гиперболы можно найти декартову систему координат такую, что гипербола будет описываться уравнением
:
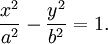
Числа 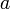 и и 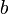 называются соответственно вещественной
и мнимой полуосями
гиперболы. называются соответственно вещественной
и мнимой полуосями
гиперболы.
Свойства гиперболы:
· Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох
для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу
). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.
· Каждая гипербола имеет пару асимптот: 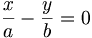 и и 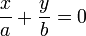 . .
· Расстояние от начала координат до одного из фокусов гиперболы называют фокусным расстоянием
гиперболы  . .
· Эксцентриситетом
гиперболы называется величина е = с / а.
Эксцентриситет гиперболы e
> 1
· Расстояние от вершины гиперболы до асимптоты вдоль направления параллельного оси ординат называется малой
или мнимой полуосью
гиперболы 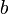 . .
· Расстояние от фокуса до гиперболы вдоль прямой, параллельной оси ординат называется фокальным параметром
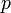 .. ..
Список литературы:
Канатиков А.Н., Крищенко А.П.
Аналитическая геометрия: Учеб. для вузов. 2-е изд. / Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2000 – 388с.(Сер. Математика в техническом университете; Вып. III ).
http ://
www .
Wikipedia .
ru
|