Курсовая работа:
Режим переконденсации с компактным распределением размеров капель.
Описание проблемы и постановка задачи.
Классические работы Дж.Гиббса, М.Фольмера, Ф.Беккера, В.Дёринга, Я.Френкеля, Я.Зельдовича по физике фазовых переходов I рода относятся к ранним стадиям зарождения новой фазы.
В данной же работе нас интересует процесс конденсации, переходящий из флуктуационного режима роста зародышей новой фазы в стадию переконденсации, именуемую также коалесценцией, или Оствальдовским созреванием [
[i]
], когда рост крупных капель происходит за счёт растворения более мелких (при условии, что все капли далеки друг от друга).
Режим переконденсации может проходить в одном случае под управлением поглощающей способности поверхности (теория Вагнера: [ [ii]
]), когда длина свободного пробега 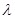 молекулы много больше радиуса капли молекулы много больше радиуса капли 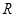 , а в другом случае под управлением диффузии в паре (теория Лифшица-Слёзова: [ [iii]
, [iv]
]), когда , а в другом случае под управлением диффузии в паре (теория Лифшица-Слёзова: [ [iii]
, [iv]
]), когда 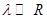 . .
Причиной расхождения эксперимента с теорией Лифшица-Слёзова-Вагнера оказалось допущение неограниченного объёма кластеров новой фазы [ [v]
].
Поэтому все дальнейшие теоретические исследования Оствальдовского созревания предполагают компактное основание распределения капель по размерам [ [vi]
, [vii]
, [viii]
].
Поэтому задачей данной работы является описание уравнений и параметров режима переконденсации в условиях существования максимального размера капли.
Коалесценция имеет большое практическое значение, например, в образовании и стабильности поверхностей [ [ix]
, [x]
, [xi]
].
Описание проблемы и постановка задачи. 1
Оглавление . 2
1). Переписывание уравнений в терминах максимальной капли. 3
2). Соотношения интегральных моментов функции распределения. 5
3). Нахождение автомодельной функции распределения. 6
4). Нормировка функции распределения. 9
5). Предельный случай – распределение Лифшица-Слёзова. 10
6). Графики. 11
7). Литература. 12
8) Ссылки . 12
1). Переписывание уравнений в терминах максимальной капли.
Оригинальные уравнения теории переконденсации записываются в терминах отношения безразмерного радиуса капли к её критическому радиусу в зависимости от безразмерного времени: 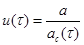 . Наша задача – переписать их в терминах отношения радиуса капли к максимальному радиусу: . Наша задача – переписать их в терминах отношения радиуса капли к максимальному радиусу: 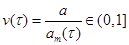 . .
Уравнение роста радиуса капли в режиме коалесценции Лифшица-Слёзова:
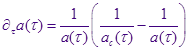
Тогда уравнение непрерывности для функции распределения по размерам капель:
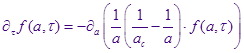
Подставляем сюда асимптотический анзац Лифшица-Слёзова в новых переменных и с явной зависимостью от времени:
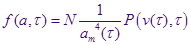
Преобразуем дифференциальное уравнение (обозначая 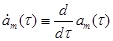 ): ):
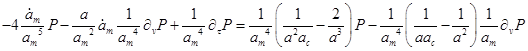
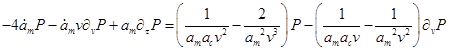
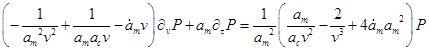
Введём
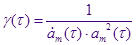
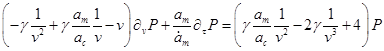
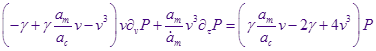
Избавимся от 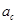 , подставив , подставив 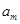 в уравнение роста радиуса капли : в уравнение роста радиуса капли :
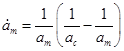 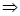 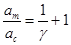
С учётом этого, а также определения 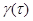 в , докажем, что в , докажем, что 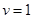 является корнем кубического полинома: является корнем кубического полинома:
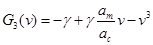
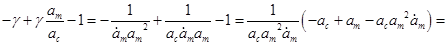
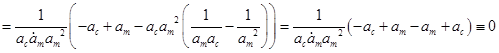
Тогда окончательно запишется следующим уравнением на функцию распределения:
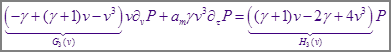
Зная один корень, найдём делением по схеме Горнера квадратичное выражение в 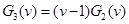
остаток = нулю
Таким образом:
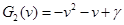
Решим квадратное уравнение, полагая корни существующими:
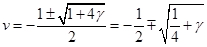
Тем самым мы разложили на множители 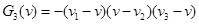 , где , где
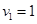 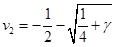 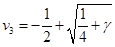 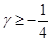
Каждая скобка в таком виде разложения, как мы увидим далее, будет положительна. Заметим также, что 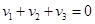 (так что (так что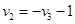 ), что, впрочем, сразу следует из теоремы Виета для ), что, впрочем, сразу следует из теоремы Виета для 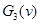 по отсутствию квадратичного члена. по отсутствию квадратичного члена.
Итак, уравнение запишется следующим образом:
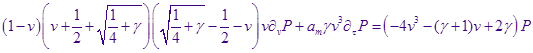
В этой работе мы рассмотрим автомодельную функцию 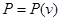 , не зависящую явно от времени, при этом в полученном дифференциальном уравнении опускается член , не зависящую явно от времени, при этом в полученном дифференциальном уравнении опускается член 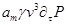 с частной производной по времени от функции распределения. с частной производной по времени от функции распределения.
2). Соотношения интегральных моментов функции распределения.
Соотношения между интегральными моментами функции распределения можно найти, не зная её явного вида. Для этого проинтегрируем от 0 до 1 левую и правую части дифференциального уравнения , опуская член с производной по времени и вводя моменты:
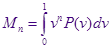
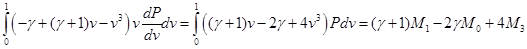
Интегрируем по частям левую часть:
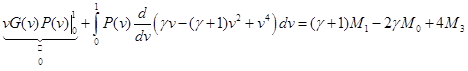
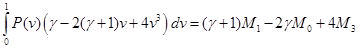
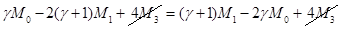
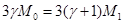
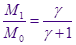
Это выражение, в сущности, означает, что 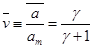 , а если вспомнить отношение между максимальным и критическим радиусами капли, то получим равенство среднего и критического радиусов: , а если вспомнить отношение между максимальным и критическим радиусами капли, то получим равенство среднего и критического радиусов:
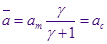
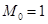 , когда функция распределения нормирована на единицу (см. пункт 4
) , когда функция распределения нормирована на единицу (см. пункт 4
)
3). Нахождение автомодельной функции распределения.
По-прежнему полагая автомодельным 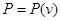 и убирая в член с производной по времени, можно явно решить дифференциальное уравнение интегрированием: и убирая в член с производной по времени, можно явно решить дифференциальное уравнение интегрированием:
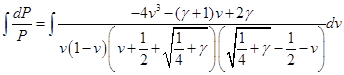
Для этого разложим подынтегральное выражение на простейшие дроби и найдём коэффициенты:
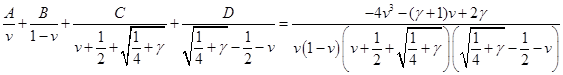
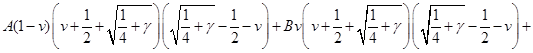
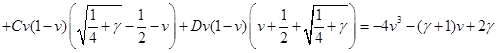
При 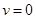 : :
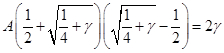 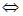 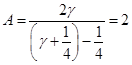
При 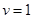 : :
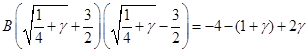 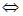 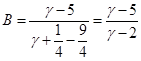
Приравнивание коэффициентов при 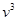 : :
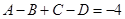 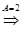 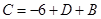
Приравнивание коэффициентов при 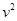 (находим (находим 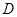 ): ):
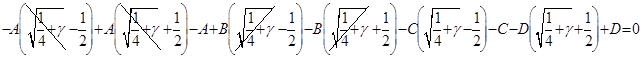
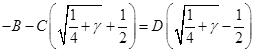
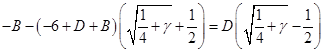
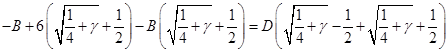
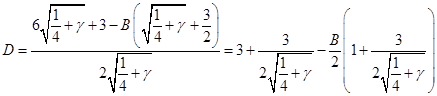
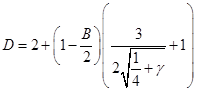
Подставляя полученное выражение для 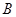 , выразим , выразим 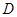 только через только через 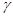 и избавимся от иррациональности в знаменателе: и избавимся от иррациональности в знаменателе:
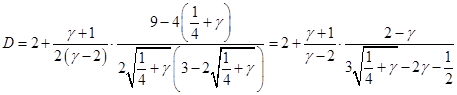
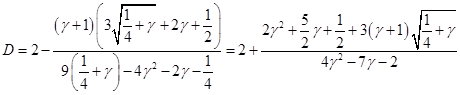
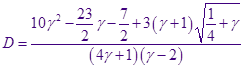
Таким образом, найдены все коэффициенты в разложении на простые дроби подынтегрального выражения в , интегрируя их, получаем, помня об области определения переменных:
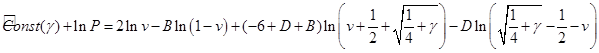
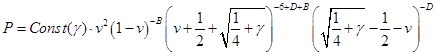
В значениях  (третий корень (третий корень 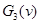 ) из окончательно запишем: ) из окончательно запишем:
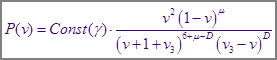
Где в силу физической ограниченности функции распределения на конце интервала, полагаем:
 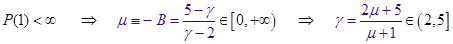
Оценим выражение для 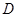 из : из :
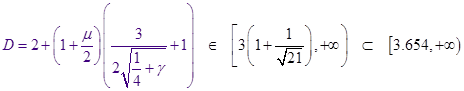
Дифференцированием и грубой оценкой можно увидеть, что 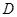 монотонно убывает по монотонно убывает по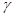 из бесконечности, как и из бесконечности, как и 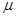 . При этом величина . При этом величина 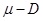 , фигурирующая в , остаётся ограниченной (не имеет особенности при , фигурирующая в , остаётся ограниченной (не имеет особенности при 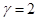 ), более того почти постоянной в заданном интервале ), более того почти постоянной в заданном интервале 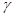 , в чём можно убедиться, вычитая , в чём можно убедиться, вычитая 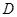 в форме из в форме из 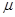 и выражая всё через и выражая всё через 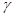 : :
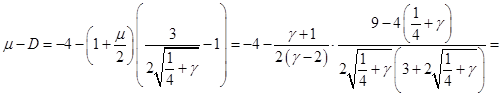
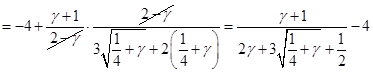
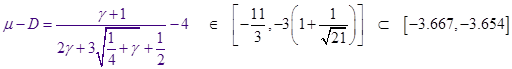
4). Нормировка функции распределения.
Как в пункте 2
проинтегрируем от 0 до 1 левую и правую части (без члена с производной по времени), предварительно разделив их на 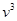 : :
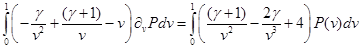
Формально интегрируем по частям левую часть:
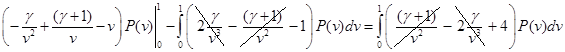
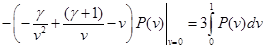
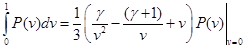
Удовлетворяя условию нормировки, подставим 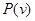 из . При из . При 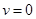 сохранится только первый член: сохранится только первый член:
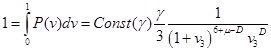
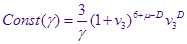
Так что функция распределения в нормированном виде равна:
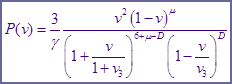
Из самого ( / ) дифференциального уравнения легко выписать производную функции распределения:
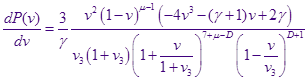
Приравняв её нулю и решая каноническое кубическое уравнение 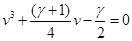 по формуле Кардано, имеем для максимума функции распределения, изменяющего своё положение с изменением по формуле Кардано, имеем для максимума функции распределения, изменяющего своё положение с изменением 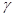 : :
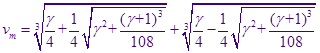
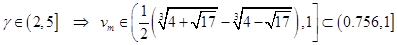
5). Предельный случай – распределение Лифшица-Слёзова.
Рассмотрим предельный случай при  . При этом из . При этом из 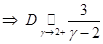 , а из , а из 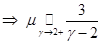 . Тогда как их разность . Тогда как их разность 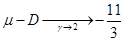 , что было показано в . Нам также пригодится асимптотика: , что было показано в . Нам также пригодится асимптотика: 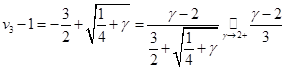
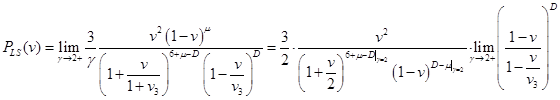
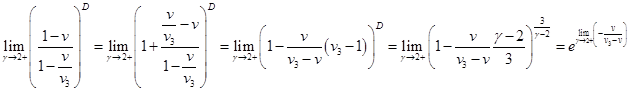
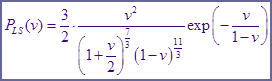
Приведём для сравнения функцию Лифшица-Слёзова, записанную в оригинальных переменных 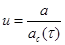 : :
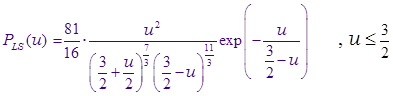

Здесь нарисованы функции распределения 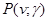 из , охватывающие весь интервал возможных из , охватывающие весь интервал возможных 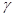 вплоть до функции Лифшица-Слёзова . вплоть до функции Лифшица-Слёзова .
Литература.
1. А.Н.Васильев, А.К.Казанский, Л.Ц.Аджемян: « Переконденсация пересыщенного пара: аналитические теории и численный эксперимент
».
2. П.Губанов, Ю.Желтов, И.Максимов, В.Морозов: « Кинетический кроссовер режимов коалесценции в пересыщенном однородном растворе
».
3. В.Бойко, Х.Могель, В.Сысоев, А.Чалый « Особенности метастабильных состояний при фазовых переходах жидкость-пар
»
4. В.Ф.Разумов: « Курс лекций по синергетике
».
5. Е.М.Лифшиц, Л.П.Питаевский: « Физическая кинетика
».
6. B.Giron, B.Meerson, P.V.Sasorov: « Weak selection and stability of localized distributions in Ostwald ripening
».
7. V.M.Burlakov: « Ostwald Ripening on nanoscale
».
8. B.Niethammer, R.L.Pego: « Non-self-similar behavior in the LSW theory of Ostwald ripening
».
Перечисленные и многие другие материалы по теме временами доступны по ftp здесь: ftp :// rodion . homeftp . net Work Work =Учёба= =Учёба=  Кафедра статфизики Кафедра статфизики  =Курсовая= =Курсовая=  Литература Литература
Ссылки
[i]
W.Z.Ostwald // Phys. Chem.
37
, 385 (1901)
[ii]
C.Z.Wagner // Electrochem.
65
, 581 (1961)
[iii]
М . Лифшиц , В . Слёзов // ЖЭТФ
35
, 479 (1958)
[iv]
M.Lifshitz, V.Slyozov // J.Phys.Chem.Solids
19
, 35 (1961)
[v]
J. Alkemper, V.Snyder, N.Akaiwa, P.Voorhees // Phys.Rev.Lett.
82
, 2725 (1999)
[vi]
N.Akaiwa, P.Voorhees // Phys.Rev.B
49
, 3860 (1994)
[vii]
D.Fan, S.Chen, L.Chen, P.Voorhees // ActaMaterialia
50
, 1895 (2002)
[viii]
K.Wang, M.Gliksman, K.Rajan // Comput.Mat.Sci.
34
, 235 (2005)
[ix]
S.Kukushkin, A.Osipov // Progress in Surf. Sci.
51
, 1 (1996)
[x]
M.Zinke-Allmang, L.Feldman, M.Grabow // Surf. Sci.Rep.
16
, 377 (1992)
[xi]
W. Bartelt, C.Theis, M.Tromp // Phys.Rev. B
54
, 11741 (1996)
|