| Московский Авиационный Институт
(Государственный Технический Университет)
Курсовая работа по дисциплине
“Теория вероятностей и математическая статистика”
Тема: «Исследование случайных явлений вероятностно-статистическими методами»
Учебная группа №М11
Выполнил студент:
Ульянов С.А.
Руководитель КР:
профессор Виноградов С.А.
Серпухов,2008
Оглавление
1. Введение
2. Решения заданий
a) Задача №1
b) Задача №2
c) Задача №3
d) Задача №4
e) Задача №5
f) Задача №6
g) Задача №7
h) Задача №8
i) Задача №9
j) Задача №10
3. Вывод
4. Список использованной литературы
Введение
Теория вероятностей и математическая статистика имеет огромное значение в современном мире.
Изучение действительности в её сложности и многообразии требует рассмотрения наиболее существенных связей. Окружающее нас пространство состоит из массовых явлений и процессов. Многие отдельные факты и события зависят от законов случая, но массы их подчиняются особым закономерностям, в частности, статистическим и вероятностным. Факты в силу своей же индивидуальности с одной стороны, отличаются друг от друга, а с другой стороны имеют нечто общее.
Целями данной курсовой работы являются:
а) закрепление и углубление теоретических и практических знаний, полученных на лекциях и других видах занятий; формирование вероятностно – статистического; аналитического мышления, необходимого для исследования сложных систем различной природы со стохастическими переменными.
б) формирование умений самостоятельно решать задачи по определению вероятностных и числовых характеристик случайных явлений с обоснованием применяемых при этом теоретических положений и анализом полученных результатов.
Данная курсовая работа имеет большое практическое значение. В ней приведены задачи, с которыми сталкивается менеджер каждый день. В результате анализа проявления экономических законов устанавливается конкретное состояние и развитие фирмы, предприятия, отрасли в целом на определённый момент или за определённый отрезок времени.
Таким образом, теория вероятностей и математическая статистика выступает важнейшим инструментом познания и использования экономических (и других общественных) законов. В ходе выполнения курсовой работы я так же применял и знания, полученные при изучении дисциплины математический анализ. Это связано с необходимостью использовать аналитико-математический аппарат.
Решение задач
Задание № 1
Для оплаты купленных товаров в супермаркете N
=6
покупателей случайным образом распределяются по m
кассам без ограничений на число покупателей в каждой кассе. Оплата каждым из N
покупателей в любой из m
=3
касс равновозможна и не зависит от длины возможной очереди (наличия свободных касс). Определить вероятность того, что:
а) во всех кассах окажется одинаковое число покупателей;
б) две кассы будут не заняты, а в остальных число покупателей будет одинаковым;
в) все покупатели будут оплачивать товары только в одной кассе;
г) хотя бы одна касса будет свободна от покупателей.
Дано: Решение
N=6 А – событие, во всех кассах одинаковое число покупателей, т.е. в каждой из m=3 трёх касс по два покупателя.
Р(А)-? В – событие, две кассы будут не заняты. а в остальных число покупателей
P(B)-? будет одинаковым, т.е. в одной кассе будут шесть покупателей
P(C)-? С – событие, все покупатели будут оплачивать товар в одной кассе, это
P(D)-? событие аналогично событию В, т.к. в одной кассе будут оплачивать товар все шесть покупателей.
D – событие, хотя бы одна касса будет свободна от покупателей.
В числителе применяем формулу гипергеометрического распределения, знаменатель вычисляется по формуле числа размещений nm
без повторений.
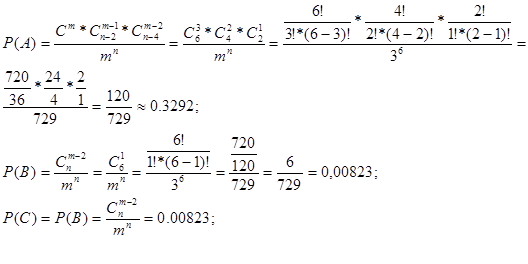
P
(
D
)=
P
1
+
P
2
,
где
Р1
–
одна касса свободна;
Р2
–
две кассы свободны;

Ответ: P(A)=0.3292; P(B)=0.00823; P(C)=0.00823; P(D)=0.2551.
Задание 2
На плоскости проведены параллельные прямые, отстоящие друг от друга на расстоянии 2
h
.
На плоскость случайным образом (на удачу) бросается тонкий стержень (игла) длиной 2
l
(l
<h
).Появление центра на отрезке 2
h
в любой его точке равновозможно, как и появление любого значения угла φ
между стержнем и прямой на интервале (0
,π
).
Попадание центра стержня на отрезок 2
h
и угловая ориентация φ
стержня – события независимые. Требуется при заданных исходных данных 2
h
и 2l
:
1.Определить вероятность того, что стержень пересечёт какую-либо прямую.
2.Методом статистических испытаний определить эмпирическое значение числа π
при заданных h
,l
и числе испытаний n
≥100, при этом представить таблицу результатов статистических испытаний с описанием условий проведения опыта.
Дано: Решение
2h=35 Для решения задачи необходимо провести опыт. заключающийся в
2l=28 подбрасывании с вращением стержня и определения количества пересече-
P-? ний его с линиями на плоскости.
π -? Вероятность пересечения стержнем какой-либо прямой на плоскости
вычисляется классическим способом по формуле P=m/n, где
m – количество пересечений, n – количество всех бросков.
Число π рассчитывается как  . Исход опыта ( положение иглы на плоскости) описывается 2-мя координатами: х – абсцисса центра иглы относительно ближайшей прямой слева и . Исход опыта ( положение иглы на плоскости) описывается 2-мя координатами: х – абсцисса центра иглы относительно ближайшей прямой слева и  - угол. который составляет игла с прямыми. Очевидно, что все значения х и - угол. который составляет игла с прямыми. Очевидно, что все значения х и  равновозможны. Очевидно, можно ограничить возможные пересечения только с одной (ближайшей левой) прямой. Прямоугольник на плоскости х0 равновозможны. Очевидно, можно ограничить возможные пересечения только с одной (ближайшей левой) прямой. Прямоугольник на плоскости х0 со сторонами L/2 и π/2 представляет пространство элементарных событий Ω; со сторонами L/2 и π/2 представляет пространство элементарных событий Ω;  . Если абсцисса х центра иглы будет меньше, чем . Если абсцисса х центра иглы будет меньше, чем  , то игла пересечёт прямую, интересующее нас событие , то игла пересечёт прямую, интересующее нас событие 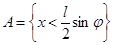 (см. Заштрихованную область на рис.) Площадь этой области равна (см. Заштрихованную область на рис.) Площадь этой области равна 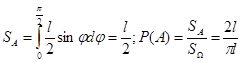 . .

Данный опыт был впервые проведён французским естествоиспытателем Ж.Л.Л. Бюффоном (1707-1788). Данный опыт я проводил в нормальных условиях при соблюдении всех размеров отрезков и длины стержня.
Таблица результатов статистических испытаний. + пересекло - не пересекло
| 1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
| +
|
+
|
+
|
-
|
+
|
-
|
+
|
+
|
-
|
+
|
-
|
-
|
-
|
+
|
+
|
| 16
|
17
|
18
|
19
|
20
|
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
| +
|
-
|
+
|
-
|
+
|
+
|
+
|
+
|
-
|
+
|
-
|
+
|
+
|
-
|
-
|
| 31
|
32
|
33
|
34
|
35
|
36
|
37
|
38
|
39
|
40
|
41
|
42
|
43
|
44
|
45
|
| -
|
+
|
+
|
+
|
+
|
+
|
-
|
+
|
-
|
+
|
-
|
-
|
+
|
-
|
+
|
| 46
|
47
|
48
|
49
|
50
|
51
|
52
|
53
|
54
|
55
|
56
|
57
|
58
|
59
|
60
|
| +
|
+
|
-
|
-
|
+
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
+
|
-
|
-
|
| 61
|
62
|
63
|
64
|
65
|
66
|
67
|
68
|
69
|
70
|
71
|
72
|
73
|
74
|
75
|
| -
|
+
|
-
|
+
|
+
|
+
|
-
|
-
|
+
|
+
|
+
|
-
|
-
|
+
|
+
|
| 76
|
77
|
78
|
79
|
80
|
81
|
82
|
83
|
84
|
85
|
86
|
87
|
88
|
89
|
90
|
| +
|
+
|
+
|
-
|
+
|
+
|
+
|
-
|
-
|
+
|
-
|
-
|
-
|
+
|
-
|
| 91
|
92
|
93
|
94
|
95
|
96
|
97
|
98
|
99
|
100
|
101
|
102
|
103
|
104
|
105
|
| -
|
-
|
+
|
-
|
-
|
+
|
-
|
-
|
+
|
-
|
-
|
+
|
-
|
+
|
-
|
| 106
|
107
|
108
|
109
|
110
|
111
|
112
|
113
|
114
|
115
|
116
|
117
|
118
|
119
|
120
|
| -
|
+
|
+
|
+
|
-
|
+
|
-
|
+
|
-
|
+
|
+
|
+
|
-
|
+
|
+
|
| 121
|
122
|
123
|
124
|
125
|
126
|
127
|
128
|
129
|
130
|
131
|
132
|
133
|
134
|
135
|
| -
|
+
|
-
|
+
|
+
|
-
|
+
|
+
|
-
|
-
|
-
|
+
|
-
|
-
|
+
|
| 136
|
137
|
138
|
139
|
140
|
141
|
142
|
143
|
144
|
145
|
146
|
147
|
148
|
149
|
150
|
| -
|
+
|
-
|
+
|
-
|
+
|
-
|
+
|
-
|
+
|
-
|
-
|
+
|
+
|
+
|
| 151
|
152
|
153
|
154
|
155
|
156
|
157
|
158
|
159
|
160
|
161
|
162
|
163
|
164
|
165
|
| +
|
+
|
-
|
+
|
-
|
-
|
-
|
+
|
+
|
-
|
+
|
-
|
+
|
+
|
+
|
| 166
|
167
|
168
|
169
|
170
|
171
|
172
|
173
|
174
|
175
|
176
|
177
|
178
|
179
|
180
|
| +
|
-
|
+
|
+
|
-
|
-
|
+
|
-
|
+
|
-
|
-
|
+
|
-
|
-
|
-
|
| 181
|
182
|
183
|
184
|
185
|
186
|
187
|
188
|
189
|
190
|
191
|
192
|
193
|
194
|
195
|
| -
|
-
|
-
|
+
|
-
|
-
|
+
|
-
|
-
|
-
|
+
|
-
|
-
|
+
|
-
|
| 196
|
197
|
198
|
199
|
200
|
201
|
202
|
203
|
204
|
205
|
206
|
207
|
208
|
209
|
210
|
| -
|
-
|
-
|
-
|
+
|
+
|
-
|
-
|
-
|
+
|
-
|
+
|
-
|
+
|
+
|
Всего бросков произвёл 210, из них не пересекло 107 раз, пересекло 103 раза.
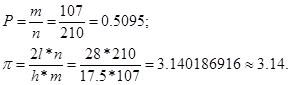
Как видно из результатов, полученное число π верно до сотого знака после запятой, что говорит об удачном исходе опыта.
Ответ: 1) р=0,5095;
2) π≈3,14.
Задание №3
Структурная схема системы доведения информации об экономических угрозах до руководства некоторой фирмы имеет вид:
      
 
 Отказы структурных элементов системы - события независимые. Известны вероятности передачи информации i-м элементом системы, Pi (i=1,…,6).Оценить надежность системы доведения информации по показателю “вероятность безотказной работы системы”.

Решение
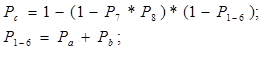


Ответ: вероятность того, что информация об угрозе дойдёт до топ-менеджера составляет 0,8781, т.е. в 8781 из 10000 случаев информация окажется у топ-менеджера.
Задание №4
В группе N
студентов, из них n
студентов являются отличниками, m
-учатся на хорошо и k
-на удовлетворительно. Предполагается, что на экзамене отличники могут получить только отличные оценки, хорошисты с равной вероятностью - оценки “хорошо” и ”отлично”, успевающие на удовлетворительно могут получить с равной вероятностью оценки“4”,“3”, “2”. На экзамен на удачу вызвали три студента. Найти вероятность того, что они получат оценки ”отлично”, «хорошо”, «удовлетворительно”.

Решение
A – событие вызванные трое студентов получат оценки 5,4,3, возможно при следующих гипотезах:
Н1
– вызваны один троечник, один хорошист, 1 отличник;
Н2
– вызваны 1 троечник, 2 хорошиста;
Н3
- вызваны 2 троечника и 1 хорошист;
Н4
– вызваны 2 троечника и 1 отличник.
Задачу можно решить 2 – мя способами.
1) Способ 1 – классический с использованием формулы сочетания, в данном случае неудобен в связи с большими вычислениями, из-за чего эти вычисления я производил в программной среде MS Excel.
 
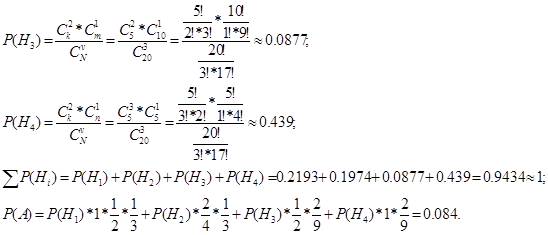
Как видно выше, сумма всех гипотез не равна в точности 1. Это связано с ошибками округления чисел вероятностей гипотез.
1/2 - вероятность хорошиста получить или оценку «хорошо», или оценку «отлично»;
1/3 – вероятность троечника получить или оценку «хорошо», или оценку «отлично», или оценку «неудовлетворительно».
1 – вероятность отличника получить оценку «отлично».
2) Способ 2 – вероятность события вычисляется классическим способом.
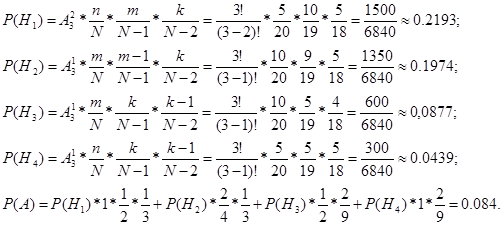
1/2 - вероятность хорошиста получить или оценку «хорошо», или оценку «отлично»;
1/3 – вероятность троечника получить или оценку «хорошо», или оценку «отлично», или оценку «неудовлетворительно».
1 – вероятность отличника получить оценку «отлично».
Ответ: Р(А)=0,084.
Задание № 5
Случайная величина  – годовой доход наугад взятого налогоплательщика. Плотность распределения вероятностей случайной величины – годовой доход наугад взятого налогоплательщика. Плотность распределения вероятностей случайной величины 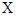 задана в виде: задана в виде:

где a – неизвестный параметр распределения, а величины b и c являются константами, значения которых заданы в таблице вариантов задания.
Требуется :
1) Определить значения параметра «а» и построить график функции f(х).
2) Найти функцию распределения F(х) и построить её график.
3) Определить математическое ожидание Mx
, дисперсию Дx
и среднее квадратическое отклонение 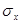 годового дохода годового дохода  . .
4) Вычислить значения третьего М3
и четвертого М4
центральных моментов, и определить коэффициенты ассиметрии и эксцесса.
5) Определить размер годового дохода Х1
в тыс. HE,., не ниже которого с вероятностью Р окажется годовой доход случайного выбранного налогоплательщика.


Решение
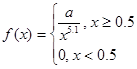
1) 
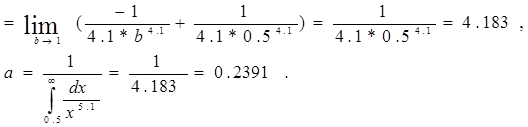

2)


3) Математическое ожидание находим по формуле:

Дисперсию проще всего искать по формуле 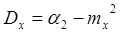 , где , где  - второй начальный момент, а само - второй начальный момент, а само
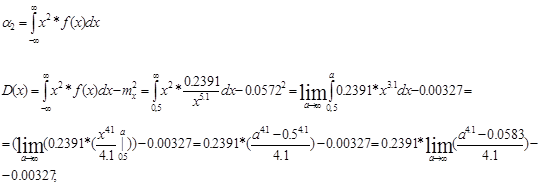
С.К.О. есть положительный квадрат от дисперсии, след.
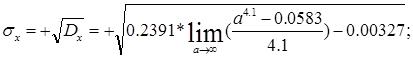
4) Находим третий и четвёртый центральные моменты по формуле через начальные моменты:
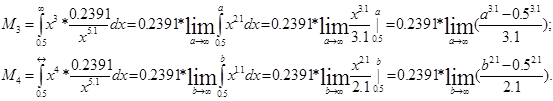
Коэффициенты ассиметрии As
, эксцесса Ex
находим по следующим формулам:
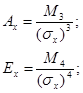
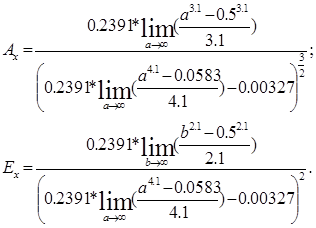
5) Для нахождения вероятности воспользуемся формулой для описания вероятност попадания СВ Х на интервал 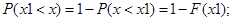
Подставляем известные значения, получаем:
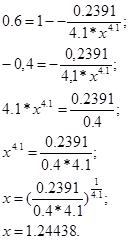
Ответ: 1) а=0,2391;
2) 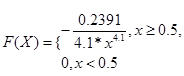 ; ;
3) 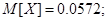
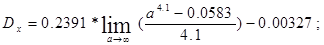

4)  ; ;
5) 
Задание № 6
Производится «n
» независимых испытаний, в каждом из которых события А
может появиться с вероятностью Р
.
Требуется
: 1)Определить вероятность того, что событие А
появится при n
– испытаниях равно k
- раз.
2)Определить вероятность того, что событие А
появится при n
– испытаниях более m
- раз.
3)Определить вероятность того, что событие А
появится при n
– испытаниях не менее k
1
- раз, но не более k
2
- раз.
4)Вычислить среднее число появления события А
при n
– испытаниях и среднее квадратическое отклонение числа появлений события А
.
5)Определить с какой вероятностью должно появляться события А
в каждом из «n
» - опытов при условии, что вероятность не появления события А
ни в одном из «n
» - опытов равна Р0
.
(Указание.
При поиске ответа только на пятый вопрос принять условие, что число появлений события А
при n
– независимых опытах распределено по закону Пуассона).

Решение
1) Применяем формулу Пуассона, т.к. n – велико, р – не мало.
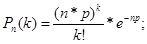
Подставляем, получаем:
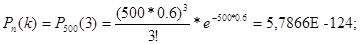
2) 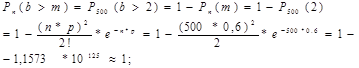
3) Использую интегральную формулу Муавра-Лапласа, потому что  . .

4) Находим МОЖ по следующей формуле 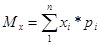 . Ввиду больших вычислений расчёт значений произвёл в программном продукте MS Excel. . Ввиду больших вычислений расчёт значений произвёл в программном продукте MS Excel.

Среднее квадратическое отклонение находим через дисперсию по формуле:

5) Так как число появлений события А
при n
– независимых опытах распределено по закону Пуассона, то:

Ответ: 1) 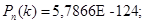
2) 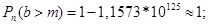
3) 
4) 
5) 
Задание № 7
Дискретная двумерная случайная величина (X
,
Y
) описывается законом распределения вероятностей, заданного рядом распределения вероятностей, представленным в таблице:
X
Y
|
X1
|
X2
|
| Y1
|
P11
|
P12
|
| Y2
|
P21
|
P22
|
| Y3
|
P31
|
P32
|
Требуется:
1. Определить законы распределения компонент случайного вектора X
и Y
соответственно.
2. Определить условный закон распределения случайной величины X
при условии, что Y
приняла значение yj
.
3. Определить условный закон распределения случайной величины Y
при условии, что X
приняла значение xi
.
4. Определить математические ожидания и дисперсии компонент случайного вектора X
и Y
.

Решение
| X
Y
|
X1
|
X2
|
Px
|
| Y1
|
P11=0,11
|
P12=0,14
|
0.25
|
| Y2
|
P21=0,16
|
P22=0,24
|
0.4
|
| Y3
|
P31=0,19
|
P32=0,16
|
0.35
|
| Py
|
0.46
|
0.54
|
1
|
1) Законы распределения компонент случайного вектора X
и Y
вычисляются с помощью складывания вероятностей, находящихся на одной строке – для х, на одном столбце –
для у.
Как видно из таблицы, сумма вероятностей, как и по х, так и по у равна 1.
2) Условный закон распределения случайной величины X
при условии, что Y
приняла значение y
1
определяется как:
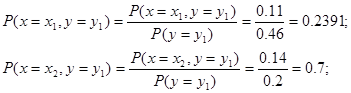
3) Условный закон распределения случайной величины Y
при условии, что X
приняла значение x
1
определяется как:

4) Математическое ожидание компонент случайного вектора X
и Y
вычисляем по формуле:

Подставляем значения, получаем:

Дисперсия компонент случайного вектора X
и Y
находиться по формуле, и равна:


Ответ: 1) Законы распределения компонент случайного вектора X
см. в таблице в левом столбце;
законы распределения компонент случайного вектора Y
см. в таблице в нижней строке.
2) 
3) 
4) 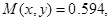 
Задание № 8
Случайная величина Y
связана со случайными величинами xi
(i= 1,…,3) функциональной зависимостью вида  . .
Известны математические ожидания случайных величин  и средние квадратические отклонения, и средние квадратические отклонения, 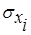 Задана также нормированная корреляционная матрица: Задана также нормированная корреляционная матрица:

Требуется:
1. Вычислить математическое ожидание случайной величины Y
.
2. Вычислить среднее квадратическое отклонение случайной величины Y
.
3. В предположении нормального закона распределения случайных величин xi
записать выражение для плотности распределения случайной величины Y
.
Дано:



mx
1
=2.0, mx2=1.9, mx
3
=1.6;
 =0.8, =0.8, 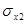 =2.1, =2.1, 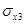 =3.2; =3.2;
Найти:
1)M[Y]-?;
2)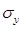 -?; -?;
3)f(Y)-?.
Решение
1) В данной задаче применяется 3-й тип постановки задачи. т.к. по известным числовым характеристикам случайных аргументов необходимо найти численные характеристики функций случайных аргументов. Учитывая, что задана линейная функция 3-х случайных аргументов, то для решения задачи применил теорему о математическом ожидании дисперсии линейной функции.
 
2) Находим корреляционный момент через коэффициент корреляции. Он необходим для расчёта дисперсии, из которой можно будет получить среднее квадратическое отклонение.

3) В предположении нормального закона распределения случайных величин xi
выражение для плотности распределения случайной величины Y
имеет вид:
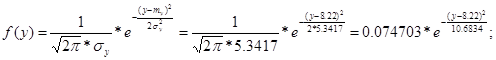
Ответ: 1) 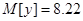 ; ;
2) 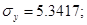
3) 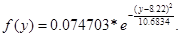
Задание №9
Пусть Х – время задержки момента начала матчей на данном стадионе. Известно среднее значение времени задержки, которое составляет «а» минут.
Требуется:
Оценить вероятность того, что начало матча будет задержано не менее, чем на t минут. Найти минимальное значение времени задержки начала матча t0
, при котором вероятность задержки на время не менее t0
не превышает требуемого значения Ртр
, если дополнительно известно, что среднее квадратичное отклонение времени задержки начала матчей Найти минимальное значение времени задержки начала матча t0
, при котором вероятность задержки на время не менее t0
не превышает требуемого значения Ртр
, если дополнительно известно, что среднее квадратичное отклонение времени задержки начала матчей  секунд. секунд.
Решение
1) Для нахождения вероятности того, что начало матча будет задержано не менее, чем на 2,5 минуты необходимо применить 1-е неравенство П.Л.Чебышева ( А.А. Маркова).
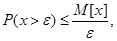 т.е. т.е. 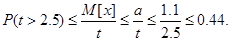
2) Минимальное значение времени задержки начала матча t0
, при котором вероятность задержки на время не менее t0
не превышает требуемого значения Ртр
, если дополнительно известно, что среднее квадратичное отклонение времени задержки начала матчей 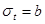 секунд вычисляется по второй теореме П.Л. Чебышева, т.к. она позволяет находить вероятность попадания случайной величины за пределы интервала от секунд вычисляется по второй теореме П.Л. Чебышева, т.к. она позволяет находить вероятность попадания случайной величины за пределы интервала от 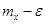 . .
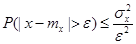 , т.е. , т.е.

Ответ: 1) Вероятность того, что мат начало матча будет задержано не менее, чем на t минут составляет не более 44%, т.е. в 1 случае из 100 начало матча будет задержано не более чем на 2,5 минуты.
2) Минимальное значение времени задержки начала матча t0
, при котором вероятность задержки на время не менее t0
не превышает требуемого значения Ртр
=0,4, составляет 2,4703 минуты.
Задание № 10
По заданному в таблице Приложения 4 временному ряду U=¦(T) требуется:
-построить диаграмму рассеивания; найти параметры модели линейного тренда и построить его на диаграмме рассеивания; найти параметры квадратичного тренда и построить его на диаграмме рассеивания;
-вычислить значение коэффициента детерминации;
-проверить адекватность построенных моделей по критериям случайности колебаний уровней остаточной последовательности (критерием серий или критерием поворотных точек), критерием соответствия распределения случайной компоненты нормальному закону распределения (критерием ассиметрии и эксцесса или критерием стьюдентизированного размаха), критерием проверки равенства математического ожидания случайной компоненты нулю, критерием проверки независимости значений уровней случайной компоненты (Дарбина-Уотсона);
-выполнить точечный прогноз значений зависимой переменной U по линейному и квадратичному тренду для Τ=8 и T=9;
-выполнить интервальный прогноз с использованием только линейного тренда;
-сформулировать выводы о качестве трендовых моделей.
Дано: Временной ряд:
| Время, t
|
Y
|
| 1
|
6.2
|
| 2
|
4.8
|
| 3
|
7.5
|
| 4
|
9.9
|
| 5
|
14
|
| 6
|
19
|
| 7
|
22
|
Решение:
Проведём исследование модели временного ряда, которая содержит 3 стадии:
· стадия спецификации модели тренда;
· стадия идентификации модели тренда4
· стадия верификации модели тренда.
1. Проанализируем первую стадию, т.е. спецификацию модели тренда. Суть стадии заключается в том, что подбирается математическая модель, описывающая изменение процессов во времени. Этот процесс начинается с построения диаграммы рассеивания и заканчивается подбором уравнения: линейного, степенного, экспоненциального, полиноминального и прочих. Решается вопрос о линейности (нелинейности) модели тренда и параметров этой модели (коэффициентов).
С помощью пакета программ MS Excel, учитывая исходные данные построил диаграмму рассеивания:

После на диаграмме рассеивания строится линейный и квадратичный тренды, а так же определяются уравнения и значения коэффициента детерминации R2
.
2. Стадия идентификации состоит в идентификации коэффициентов модели тренда по экспериментальным данным.
Для этого используем метод наименьших квадратов. Суть данного метода состоит в том. что сумма квадратов отклонений экспериментальных точек от сглаживающей прямой должна быть минимальной.
Уравнение прямой имеет вид:
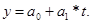
При помощи метода наименьших квадратов найдём неизвестные коэффициенты тренда а0
и а1
.
Для уравнения прямой:
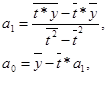
1. 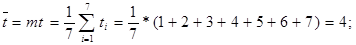
2. 
3. 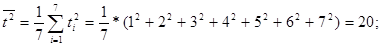
4. 
5. 
6. 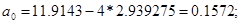
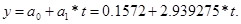
Коэффициент детерминации R2
является одной из наиболее эффективных оценок регрессионной модели, мерой свойства уравнения регрессии, характеристикой практической силы регрессионной модели.
 где где
 - сумма квадратов отклонений, обусловленная регрессией. - сумма квадратов отклонений, обусловленная регрессией.
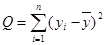 - общая сумма квадратов отклонений зависимой переменной yi
от среднего значения. - общая сумма квадратов отклонений зависимой переменной yi
от среднего значения.
 - значение зависимой переменной, найденное по уравнению регрессии. - значение зависимой переменной, найденное по уравнению регрессии.
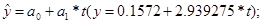
Результаты расчёта 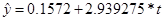 занесём в отдельную таблицу занесём в отдельную таблицу
| Время, t
|
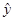
|
| 1
|
3,096475
|
| 2
|
6,03575
|
| 3
|
8,975025
|
| 4
|
11,9143
|
| 5
|
14,853575
|
| 6
|
17,79285
|
| 7
|
20,732125
|

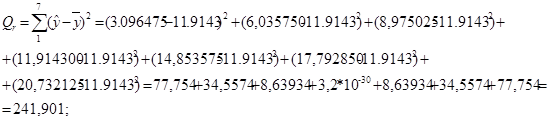

Величина коэффициента детерминации показывает, какая доля зависимой переменной у обусловлена независимой переменной t. Чем ближе R2
к 1, тем лучше регрессия аппроксимирует эмпирические данные. В нашем случае R2
=1,08759≈1, следовательно, полученное уравнение регрессии можно считать вполне достоверным и эффективно оценивающем адекватность регрессионной модели.
Для уравнения параболы:
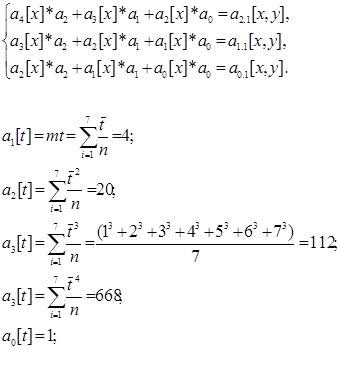
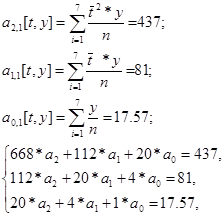


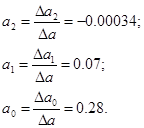
Уравнение квадратичного тренда имеет вид:
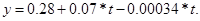
Время, t
|
y
|
| 1
|
0,3497
|
| 2
|
0,4193
|
| 3
|
0,4890
|
| 4
|
0,5586
|
| 5
|
0,6283
|
| 6
|
0,6980
|
| 7
|
0,7676
|
Ввиду того, что значения квадратичного тренда крайне малы, я построил его на отдельном графике.

3. Этап верификации модели тренда состоит в проверке адекватности модели реальным экспериментальным данным. На этой стадии производится:
- критерий Фишера для проверки гипотезы (Н0
) о значимости коэффициента детерминации R2
,
- критерий поворотных точек,
- критерий ассиметрии и эксцесса по Стьюденту.
1. Значимость коэффициента детерминации определяется критерием Фишера.
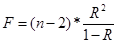 , ,
Для линейного уравнения:
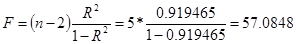 . .
Расчётное значение критерия Фишера сравнивается с табличным. При заданном уровне значимости гипотезы Н=0,05 и степенях свободы f1
=n-1 (f1
=6) и f2
=n-m-1 (f2
=5), где n – объём выборки, m – число включённых в модель факторов табличное значение равно 4б95. Сравнивая расчётное и полученное значение, получаем. что 57,0848>4,95, значит модель адекватна исходным данным.
2. Критерий поворотных точек. С помощью этого критерия можно проверить случайность остатков модели. В соответствии с этим критерием каждый уровень ряда сравнивается с двумя соединёнными с ними. Если он больше или меньше их. то эта точка считается поворотной. Затем подсчитывается сумма поворотных точек m. В случайном ряду чисел должно выполняться строгое неравенство:
 , ,
где N – объём выборочной совокупности.
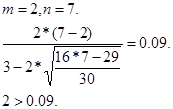
Данное условие выполняется, следовательно, можно утверждать, что ряд остатков моделей не является случайным.
3. Эксцесс характеризует относительную остроконечность или сглаженность распределения по сравнению с нормальным распределением. Положительный эксцесс означает относительно остроконечное распределение. Отрицательный эксцесс обозначает относительно сглаженное распределение.
Эксцесс я высчитал с помощью пакета программ MS Excel, он равен -1,295349862, это говорит об относительно сглаженном распределении.
Асимметрия характеризует степень нессиметричности распределения относительно его среднего. положительная асимметрия указывает на отклонение распределения в сторону положительных значений. Отрицательная асимметрия указывает на отклонение распределения в сторону отрицательных значений.
Асимметрию я рассчитал помощью пакета программ MS Excel, она равна 0,602642408, что говорит об отклонении в сторону отрицательных значений.
Учитывая вышенаписанное, можно утверждать о том, что данное распределение случайной компоненты не соответствует нормальному распределению. т.к. эти величины не малы.
Математическое ожидание равно 12.
Выполним точечный прогноз значений зависимой переменной Y по линейному тренду для t=8 и t=9.
Подставив эти значения в уравнения прямой, мы получаем, что при t=8 y= 23,6714 и для t=9 y= 26,6107.
Вывод о качестве трендовых моделей:
Все модели качественны и адекватны (пригодны для практического применения). С течением времени происходит тенденция возрастания линий трендов.
Ответ
: R2
=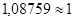 , критерий Фишера равен 57,0848, критерий поворотных точек равно 0,09, он равен -1,295349862, это говорит об относительно сглаженном распределении, асимметрия равна 0,602642408, что говорит об отклонении в сторону отрицательных значений, МОЖ равно 12, точечный прогноз значений зависимой переменной Y по линейному и квадратичному тренду при t=8 y= 23,6714 и для t=9 y= 26,6107. , критерий Фишера равен 57,0848, критерий поворотных точек равно 0,09, он равен -1,295349862, это говорит об относительно сглаженном распределении, асимметрия равна 0,602642408, что говорит об отклонении в сторону отрицательных значений, МОЖ равно 12, точечный прогноз значений зависимой переменной Y по линейному и квадратичному тренду при t=8 y= 23,6714 и для t=9 y= 26,6107.
Вывод
В ходе выполнения курсовой работы я закрепил теоретические знания и отработал практические умения, полученные на лекциях и других видах занятий, в результате чего вырабатывалось вероятностно-статистическое мышление, необходимое для исследования сложных систем различной природы со стохастическими переменными.
Данная курсовая работа формировала умение самостоятельно решать задачи по определению вероятностных и числовых характеристик случайных явлений с обоснованием применяемых при этом теоретических положений и анализом полученных результатов.
Эта курсовая работа имела большое практическое значение, т.к. решались типичные повседневные задачи, с которыми может столкнуться менеджер на работе.
Так же эта курсовая работа позволила ещё раз отработать навыки и закрепить знания, полученные при изучении дисциплины математический анализ.
Список использованной литературы
1. Вентцель Е.С. Теория вероятностей. Учебник для вузов – М.: «Высшая школа», 2000г.
2. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: «Высшая школа». – 2003 г.
3. Вентцель Е.С., Овчаров Л.А. Прикладные задачи теории вероятностей. – М.: «Радио и связь». – 1983г.
4. Виноградов С.А. и др. Теория вероятностей и математическая статистика. 5. Учебно-методическое пособие для практических занятий. МО, 1998 г.
|