Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
«КВАНТОВЫЕ СВОЙСТВА СВЕТА»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к решению задач по атомной физике
для студентов физического факультета
Ростов-на-Дону
2006
Методические указания разработаны кандидатом физико-математических наук, ассистентом кафедры нанотехнологии И.Н. Леонтьевым и кандидатом физико-математических наук, зав. кафедрой нанотехнологии Ю.И. Юзюком.
Ответственный редактор канд. физ.-мат. наук И.Н. Леонтьев
Компьютерный набор и верстка инженер Г.А. Колесников
Печатается в соответствии с решением кафедры общей физики физического факультета РГУ, протокол № 21 от 25 апреля 2006 г.
ОСНОВНЫЕ ФОРМУЛЫ
· Закон Стефана - Больцмана
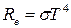 , ,
где R
е
– энергетическая светимость черного тела; Т
– термодинамическая температура; s
- постоянная Стефана – Больцмана.
· Энергетическая светимость серого тела в классическом приближении
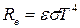 , ,
где e
– коэффициент теплового излучения (степень черноты) серого тела.
· Закон смещения Вина
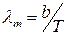 , ,
где l
m
– длина волны, на которую приходится максимум энергии излучения; b
-постоянная закона смещения Вина.
· Энергия фотона
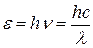 или или 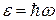 , ,
где h
– постоянная Планка; 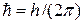 ; n – частота излучения; w
– циклическая частота; l
– длина волны. ; n – частота излучения; w
– циклическая частота; l
– длина волны.
· Формула Планка для спектральной плотности энергии
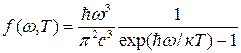 , ,
где 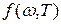 – спектральная плотность энергетической светимости черного тела; w
– круговая частота; с
– скорость света в вакууме; к
– постоянная Больцмана; – спектральная плотность энергетической светимости черного тела; w
– круговая частота; с
– скорость света в вакууме; к
– постоянная Больцмана; 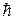 – постоянная Планка.
– постоянная Планка.
· Формула Эйнштейна для фотоэффекта
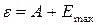 , ,
где e
– энергия фотона, падающего на поверхность металла; А
– работа выхода электрона из металла; Е
max
– максимальная кинетическая энергия фотоэлектрона.
· Коротковолновая граница lmin
сплошного рентгеновского спектра
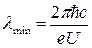 , ,
где 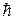 – постоянная Планка; с
– скорость света в вакууме; е
– заряд электрона; U
– разность потенциалов, приложенная к рентгеновской трубке. – постоянная Планка; с
– скорость света в вакууме; е
– заряд электрона; U
– разность потенциалов, приложенная к рентгеновской трубке.
· Давление производимое светом при нормальном падении,
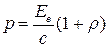 или или 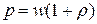 , ,
где Ee
– облученность поверхности; с
– скорость электромагнитного излучения в вакууме; w
– объемная плотность энергии излучения; r
– коэффициент отражения.
· Изменение длины волны Dl фотона при рассеянии его на свободном электроне на угол q
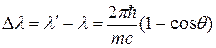 , ,
где m
– масса покоя электрона отдачи; с
– скорость света в вакууме; 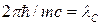 – комптоновская длина волны. – комптоновская длина волны.
Задача №1
Исследование спектра излучения Солнца показывает, что максимум спектральной плотности энергетической светимости соответствует длине волны
l
= 500 нм. Принимая Солнце за черное тело, определить: 1) энергетическую светимость Солнца; 2) поток энергии Фе
, излучаемый Солнцем; 3) массу
m
электромагнитных волн (всех длин), излучаемых Солнцем за 1 с.
Энергетическая светимость R
черного тела выражается формулой Стефана – Больцмана
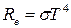 . .
Температура излучающей поверхности может быть определена из закона смещения Вина
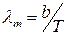 . .
Выразив отсюда температуру Т
и подставив ее в закон Стефана – Больцмана, получим
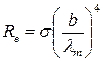 . .
Произведя вычисления по этой формуле, получим Re
= 64 МВт/м2
.
Поток энергии Фе
, излучаемый Солнцем, равен произведению энергетической светимости R
на площадь поверхности солнца S
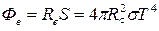 , ,
где RC
= радиус Солнца. Подставляя в последнюю формулу численные значения, получим Фе
=
3,9×1026
Вт.
Массу электромагнитных волн (всех длин), излучаемых Солнцем за время D
t
, определим, применив закон пропорциональности массы и энергии
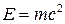 . .
С другой стороны, энергия электромагнитных волн, излучаемых за время D
t
,
равна произведению потока энергии Фе
(мощности излучения) на время
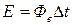 . .
Отсюда
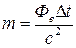 . .
Произведя вычисления, получим m
= 4,3×109
кг.
Задача №2
Вин предложил следующую формулу для распределения энергии в спектре теплового излучения:
 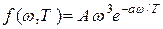 ,
,
где а = 7,64
×
10-12
К
×
с. Найти с помощью этой формулы при Т = 2000 К: а) наиболее вероятную частоту
w
вер
длину
l
вер
излучения; б) средние значения частоты <
w
>.
Наиболее вероятную частоту излучения ω
найдем из условия
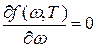 . .
Отсюда
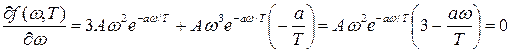 . .
Удовлетворяющие этому уравнению значения ω = 0 , ω = ∞ соответствуют минимумам функции  . Значение w, обращающее в нуль выражение, стоящее в скобках, представляет собой наиболее вероятную частоту излучения wвер . Значение w, обращающее в нуль выражение, стоящее в скобках, представляет собой наиболее вероятную частоту излучения wвер
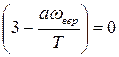 . .
Откуда 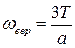 =7,8×1014
с-1
. =7,8×1014
с-1
.
2. Поскольку связь функций 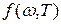 и и 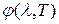 имеет следующий вид: имеет следующий вид:
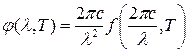 , ,
то в нашем случае
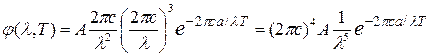 . .
Наиболее вероятную длину волны излучения найдем из условия
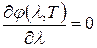 . .
Тогда
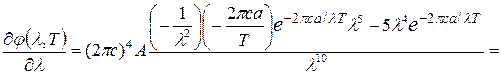
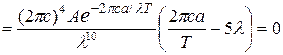 . .
Удовлетворяющие этому уравнению значения λ = 0 , λ = ∞ соответствуют минимумам функции 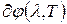 . Значение λ, обращающее в нуль выражение, стоящее в скобках, представляет собой наиболее вероятную частоту излучения λ вер
. . Значение λ, обращающее в нуль выражение, стоящее в скобках, представляет собой наиболее вероятную частоту излучения λ вер
.
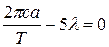 => => 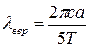 =2,40 мкм. =2,40 мкм.
Среднее значение частоты излучения определяется следующим выражением
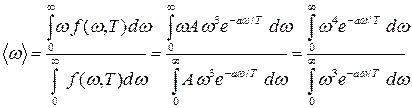 . .
Интегралы, стоящие как в числителе последней дроби, так и в знаменателе сводятся к следующему табличному интегралу:
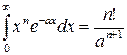 . .
Тогда
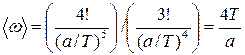 =1,05×1014
с-1
. =1,05×1014
с-1
.
Задача №3
Преобразовать формулу Планка к виду, соответствующему распределению: а) по линейным частотам; б) по длинам волн.
Энергетическая светимость абсолютно черного тела определяется следующим выражением:
 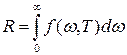 , (1) , (1)
где 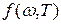 – функция спектрального распределения энергии излучения, определяемая формулой Планка – функция спектрального распределения энергии излучения, определяемая формулой Планка
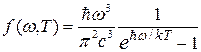 . (2) . (2)
Чтобы получить распределение по линейным частотам произведем в (1) замену переменных с учетом того, что
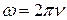 . .
Тогда
 , ,
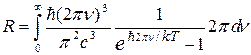 , ,
отсюда
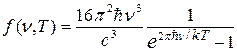 . .
Аналогичным образом поступим, чтобы найти распределение по длинам волн. Поскольку
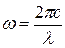 , ,
то
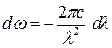 , ,
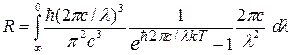 , ,
отсюда
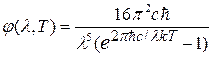 . .
Задача №4
Получить приближенные выражения формулы Планка при
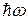 << << 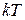 и и
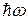 >> >> 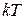 . .
Рассмотрим первый случай, когда 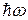 << << 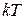 . Отсюда . Отсюда
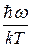 << 1. << 1.
Тогда мы можем воспользоваться следующим тождеством
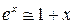 , ,
откуда
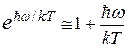 . .
Подставляя полученное выражение в формулу Планка, получим
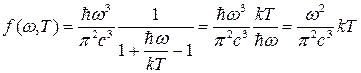 . .
Полученное выражение представляет собой закон Рэлея – Джинса.
Рассмотрим теперь случай, когда 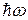 >> >> 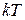 . В этом случае единицей в знаменателе формулы Планка можно пренебречь т.к. . В этом случае единицей в знаменателе формулы Планка можно пренебречь т.к.
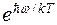 >> 1. >> 1.
Отсюда
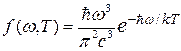 . .
Полученное выражение совпадает с законом Вина (см. задачу №2). Здесь
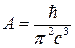 , , 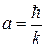 . .
Задача №5
Определить максимальную скорость фотоэлектронов
vmax
, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны
l
1
= 0,155 мкм; 2)
g
– излучением с длиной волны
l
2
= 2,47 пм.
Максимальную скорость фотоэлектронов определим из уравнения Эйнштейна для фотоэффекта
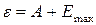 . (3) . (3)
Энергия фотона вычисляется по формуле
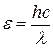 . .
Работа выхода электрона для серебра равна А
= 4,7 эВ.
Кинетическая энергия фотоэлектрона в зависимости от того, какая скорость ему сообщается, может быть выражена по классической формуле
 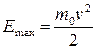 (4) (4)
или по релятивистской
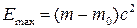 . (5) . (5)
Если энергия фотона e
много меньше энергии покоя электрона Е0
,
то может быть применена формула (4); если же e
сравнима по размеру с Е0
,
то вычисление по формуле (4) приводит к грубой ошибке, в этом случае кинетическую энергию фотоэлектрона необходимо вычислять по формуле (5).
Для ультрафиолетового излучения с длиной волны l
1
= 0,155 мкм энергия фотона равна e
1
=
8 эВ, что много меньше энергии покоя электрона (0,511 МэВ). Следовательно, в данном случае формула (4) справедлива, откуда
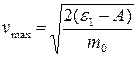 = 1,08×106
м/c. = 1,08×106
м/c.
В случае g
– излучения с длиной волны l
2
=
2,47 пм энергия фотона равна e
1
=
0,502 МэВ, тогда работой выхода электрона (А
= 4,7 эВ) можно пренебречь и можно принять, что максимальная кинетическая энергия фотоэлектрона равна энергии фотона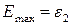 . Т.к. в данном случае энергия покоя электрона сопоставима с энергией фотона, то для вычисления скорости фотоэлектрона необходимо воспользоваться релятивистской формулой для кинетической энергии . Т.к. в данном случае энергия покоя электрона сопоставима с энергией фотона, то для вычисления скорости фотоэлектрона необходимо воспользоваться релятивистской формулой для кинетической энергии
 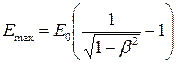 , ,
где 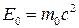 . Произведя математические преобразования, получим . Произведя математические преобразования, получим
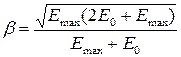 . .
Тогда максимальная скорость фотоэлектронов, вырываемых g – излучением равна
 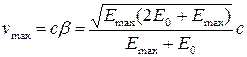 = 226×106
м/c. = 226×106
м/c.
Задача №6
До какого потенциала можно зарядить удаленный от других тел цинковый шарик, облучая его ультрафиолетовым излучением с длиной волны
l
= 200 нм.
При облучении шарика ультрафиолетовым излучением с длиной волны l, из него будут выбиваться электроны с максимальной кинетической энергией Е
max
, причём электроны будут покидать шарик до тех пор, пока энергия электростатического взаимодействия (притяжения) W
не станет равной максимальной кинетической энергии фотоэлектронов Е
max
,т. е.
W
= Е
max
.
Максимальную кинетическую энергию фотоэлектронов найдем из уравнения Эйнштейна для фотоэффекта
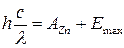 , ,
где AZn
– работа выхода электрона для цинка. Отсюда
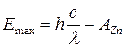 . .
Поскольку
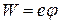 , ,
где е
– заряд электрона, j
– потенциал шарика, то
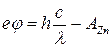 . .
Отсюда
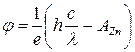 =2,74 В. =2,74 В.
Задача №7
Определить красную границу
l
кр
фотоэффекта для цезия, если при облучении его поверхности фиолетовым светом с длиной волны
l
= 400 нм максимальная скорость
vmax
фотоэлектронов равна 0,65 Мм/с..
При облучении светом, длина волны которого l
кр
соответствует красной границе фотоэффекта, скорость, а следовательно, и кинетическая энергия фотоэлектронов равны нулю. Поэтому уравнение Эйнштейна в этом случае будет иметь вид
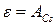 или или 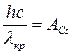 , ,
где А
Cs
– работа выхода электрона из цезия. Отсюда
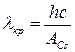 . (6) . (6)
Чтобы получить работу выхода электрона из цезия воспользуемся уравнением Эйнштейна в виде
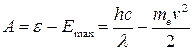 . (7) . (7)
Подставляя (7) в (6), получим
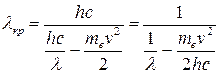 .= 651 нм. .= 651 нм.
Задача №8
После увеличения напряжения на рентгеновской трубке в
h
= 2,0 раза первоначальная длина волны
l
0
коротковолновой границы сплошного рентгеновского спектра изменилась на
D
l
= 50пм. Найти
l
0
.
Коротковолновая граница тормозного излучения сплошного рентгеновского спектра определяется выражением:
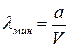 , ,
где V
– напряжение на рентгеновской трубке; а
– некоторая постоянная, то при увеличении напряжения на рентгеновской трубке длина волны рентгеновского излучения будет уменьшаться. Тогда
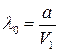 и и 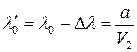 . .
Разделив второе равенство на первое, получим
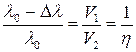 . .
Отсюда находим
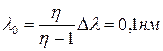 . .
Задача №9
Определить напряжение на рентгеновской трубке, если известно, что зеркальное отражение узкого пучка ее излучения от естественной грани монокристалла
NaCl
наблюдается при уменьшении угла скольжения вплоть до
a
= 4,1
°
. Соответствующее межплоскостное расстояние
d
= 281 пм.
Согласно закону Вульфа – Брэгга
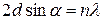 , (8) , (8)
где d
– межплоскостное расстояние, a
– угол дифракции (брэгговский угол или угол, под которым наблюдается максимум отраженного от кристалла рентгеновского пучка), l
– длина волны падающего рентгеновского излучения, n
– порядок дифракции (в данном случае n
= 1).
Коротковолновая граница тормозного излучения сплошного рентгеновского спектра определяется следующим выражением:
 , ,
где V
– напряжение на рентгеновской трубке. Подставляя последнее выражение в (8), получим
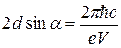 . .
Отсюда
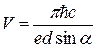 . .
Подставляя в последнее выражение численные значения, получим V
= 31 кВ.
Задача №10
Узкий пучок рентгеновского излучения с длиной волны
λ
падает на рассеивающее вещество. Найти
λ
, если длины волн смещенных составляющих излучения, рассеянного под углами
q
1
= 60° и
q
2
= 120°, отличаются друг от друга в
h
= 2,0 раза.
Изменение длины волны фотона при его рассеивании на свободном электроне равно
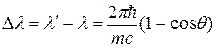 , (9) , (9)
где  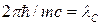 – комптоновская длина волны электрона. Тогда формула (9) для случаев рассеяния на углы q
1
и q
2
примет соответственно следующий вид: – комптоновская длина волны электрона. Тогда формула (9) для случаев рассеяния на углы q
1
и q
2
примет соответственно следующий вид:
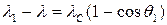 , ,
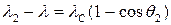 . .
По условию задачи
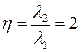 , ,
отсюда
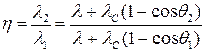 . .
Используя тригонометрическое тождество 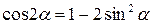 , получим , получим
 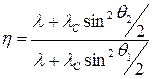 . .
Отсюда
 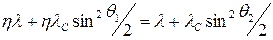
 . .
Подставляя в последнее выражение численные значения получим l
= 1,2 пм.
Задача №11
Фотон с энергией Е = 0,75 Мэв рассеялся на свободном электроне под углом
q
= 60
°
. Принимая, что кинетическая энергия и импульс электрона до соударения с фотоном были пренебрежимо малы, определить : а) энергию Е
¢
рассеянного фотона; б) кинетическую энергию электрона отдачи; в) направление его движения.
Энергию рассеянного фотона найдем, воспользовавшись формулой Комптона:
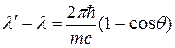 . .
Выразив длины волн l¢ и l через энергии Е
¢ и Е
соответствующих фотонов, получим
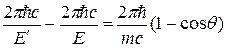 . .
Разделив обе части полученного равенства на 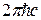 , получим , получим
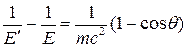 . (10) . (10)
Отсюда
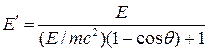 . .
Подставив численные значения величин, получим Е
¢ = 0,43 МэВ.
Кинетическая энергия электрона отдачи Ек
, как это следует из закона сохранения энергии, равна разности между энергией падающего фотона Е
и энергией рассеянного фотона Е
¢:
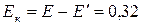 МэВ. МэВ.
Направление движения электрона отдачи можно определить воспользовавшись законом сохранения импульса, согласно которому импульс падающего фотона 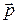 равен векторной сумме импульсов рассеянного фотона равен векторной сумме импульсов рассеянного фотона 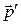 и электрона отдачи и электрона отдачи 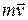 : :
  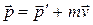 . .
Векторная диаграмма импульсов показана на рис.1. Все векторы проведены из точки О, где находился электрон в момент соударения с фотоном. Угол j определяет направление движения электрона отдачи.
Из треугольника OCD находим
Рис.1 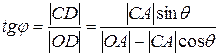
Или
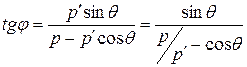
Так как 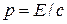 и и 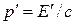 , то , то
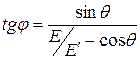 . (11) . (11)
Из (10) следует, что
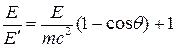 . (12) . (12)
Заменяя в (11) отношение Е/
E
¢ по формуле (12), получим
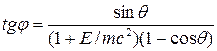 . .
Учитывая, что
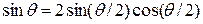 и и 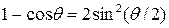 , ,
получим
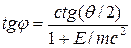 . .
Подставив численные значения, получаем 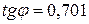 , откуда j = 35° , откуда j = 35°
Задача №12
Пучок монохроматического света с длиной волны
l
= 663 нм падает нормально на плоскую зеркальную поверхность. Поток энергии Фе
= 0,6 Вт. Определите силу
F
давления, испытываемую этой поверхностью, а также число фотонов
N
, падающих на нее за время
D
t
=5с.
Сила светового давления на поверхность равна произведению светового давления p
на площадь S
поверхности:
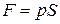 . .
Световое давление может быть найдено по формуле
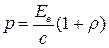 . .
Тогда
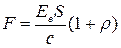 . (13) . (13)
Поскольку произведение облученности поверхности Ее
на площадь поверхности S
равно потоку Фе
энергии излучения, падающего на поверхность, то (13) можно переписать в виде
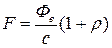 . .
После подстановки численных значений и с учетом того, что r
= 1 (поверхность зеркальная), получим F
= 4 нН.
Число фотонов, падающих за время D
t
на поверхность, определяется по формуле
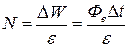 , ,
где D
W
– энергия получаемая поверхностью за время D
t
, 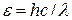 – энергия одного фотона. Отсюда
– энергия одного фотона. Отсюда
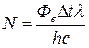 =1019
фотонов. =1019
фотонов.
Задача №13
Параллельный пучок света с длиной волны
l
= 500 нм падает нормально на зачерненную плоскую поверхность, производя давление
p
= 10 мкПа. Определить: 1) концентрацию
n
фотонов в пучке; 2) число
n
1
фотонов, падающих на поверхность площадью 1 м2
за время 1с.
Концентрация фотонов в пучке n
может быть найдена, как частное от деления объемной плотности энергии w
на энергию одного фотона e
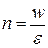 . (14) . (14)
Из формулы, определяющей давления света
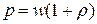 , ,
выразим w
и, подставив в (14), получим
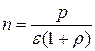
Поскольку энергия одного фотона определяется выражением
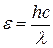 , ,
то
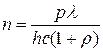
Коэффициент отражения r для зачерненной поверхности равен нулю. Тогда подставляя численные значения, получаем n
= 2,52×1013
м-3
.
Число фотонов n
1
, падающих на поверхность площадью 1 м2
за время 1с найдем из соотношения
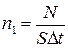 , ,
где N
– число фотонов, падающих за время D
t
на поверхность площадью S
. Но так как
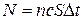 , ,
следовательно
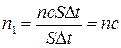 . .
После подстановки численных значений, получаем 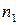 = 7,56×1021
м-2
×с-1
. = 7,56×1021
м-2
×с-1
.
Задача №14
Лазер излучает в импульсе длительностью
t
= 0,13 мс узкий пучок света с энергией Е = 10 Дж. Найти среднее за время
t
давление такого пучка света, если его сфокусировать в пятнышко диаметром
d
= 10мкм на поверхности, перпендикулярной пучку, с коэффициентом отражения
r
= 0,5.
Так как давление света определяется выражением
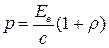 , ,
а произведение облученности поверхности Ее
на площадь поверхности S
равно потоку Фе
энергии излучения, падающего на поверхность, то
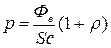 . .
Поток Фе
энергии излучения, падающего на поверхность равен
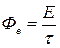 , ,
тогда с учетом того, что
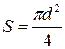 , ,
получим
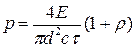 . .
Подставляя численные значения, получим р = 5 МПа ~ 50 атм.
ОСНОВНЫЕ ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ
| Постоянная Планка
|
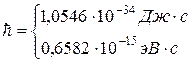
|
| Скорость света в вакууме
|
с
= 2,998×108
м/c
|
| Масса электрона
|
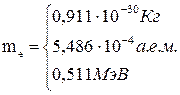
|
| Заряд электрона
|
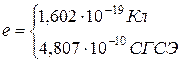
|
| Электрическая постоянная
|
eo
= 8,85×10-12
Ф/м
1/4peo
=9×109
м / Ф
|
| Постоянная Стефана - Больцмана
|
s
= 5,67×10-8
Вт/(м2
×К4
)
|
| Постоянная закона смещения Вина
|
b
= 2,90×10-3 м
×К
|
| Постоянная Больцмана
|
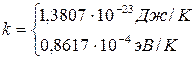
|
ЛИТЕРАТУРА
1. Иродов И.Е. Задачи по квантовой физике: Учебное пособие для физ. спец. вузов. – М.: Высшая шк., 1991. – 175с.
2. Иродов И.Е. Квантовая физика. Основные законы: Учебное пособие для вузов. – М.: Лаборатория Базовых Знаний, 2001. – 271с.
3. Трофимова Т.И., Павлова З.Г.: Сборник задач по курсу физики с решениями: Учебное пособие для вузов. Изд. седьмое, стереотипное– М.: Высшая шк., 2006. – 591с.
4. Чертов А.Г, Воробьев А.А. Задачник по физике. Изд. пятое, переработанное и дополненное – М.: Высшая шк., 1988. – 527с.
5. Борн М. Атомная физика. – М.: «Мир», 1970. – 483с.
6. Савельев И.В. Курс общей физики. Т.3 - М.: Наука., 1982. – 304с.
7. Савельев И.В. Сборник вопросов и задач по общей физики. - М.: Наука, 1982. –271с.
|