| КГБОУ СПО
«Сосновоборский автомеханический техникум»
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
и контрольные задания для студентов заочной формы обучения
на базе основного общего образования ( 9 классов )
2008
СОГЛАСОВАНО УТВЕРЖДАЮ
ЗАМ.директора по УМР
Протокол №____от ____________ Л.С.Корсакова
«___»________2008 «___»____________2008
Методические указания составлены
в соответствии с примерной программой по математике,
Государственными требованиями к минимуму
содержания и уровню подготовки выпускников
на базе среднего (полного) общего
образования.
Составитель : Петрова Н.Г.
СОДЕРЖАНИЕ :
1. Пояснительная записка.
2. Программа.
3. Методические указания .
4. Контрольные задания.
5. Литература
6. Экзаменационный материал ( тесты ).
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
.
Настоящее методическое пособие предназначено для студентов заочной формы обучения на базе основного общего образования (9 классов ) по дисциплине математика .
Данное методическое пособие ставит своей целью оказание помощи студентам-заочникам в организации их работ по овладению системой знаний и умений в объеме действующей программы по математики на базе среднего (полного) общего образования. Учебная дисциплина «Математика» является естественнонаучной , формирующей базовые знания для освоения общепрофессиональных и специальных дисциплин.
В результате изучения дисциплины студент должен :
иметь представления :
- о роли математики в современном мире, общности ее понятий и представлений ;
знать и уметь:
-использовать математические методы при решении прикладных задач.
Рабочая программа по математике рассчитана на 312 часов из них 93,6 час. на теоретические занятия и 218,4 час. на самостоятельную учебную нагрузку студенту. Программа по математике состоит из 14 разделов.
Раздел 1 «Действительные числа»
Раздел 2 «Тригонометрические выражения»
Раздел 3 «Тригонометрические функции»
Раздел 4 «Тригонометрические уравнения»
Раздел 5 «Производная»
Раздел 6 «Применение производной»
Раздел 7 «Показательная и логарифмическая функции»
Раздел 8 «Интеграл»
Раздел 9 «Аксиомы стереометрии и их простейшие свойства»
Раздел 10 «Параллельность прямых и плоскостей»
Раздел 11 «Перпендикулярность прямых и плоскостей»
Раздел 12 «Декартовы координаты»
Раздел 13 «Многогранники, объем многогранников»
Раздел 14 «Тела вращения, объем тел вращения, площади поверхности тел вращения»
Основной формой учебного процесса является индивидуальная самостоятельная работа с учебной литературой
Изучать дисциплину математика необходимо в логической последовательности:
1. Усвоить учебные материалы , согласно программы.
2. Составить ответы на вопросы для самоконтроля.
3. Выполнить контрольную работу.
4. Сдать промежуточную аттестацию в виде экзамена.
Все непонятные вопросы студент может выяснить в индивидуальной консультации у преподавателя.
В соответствии с учебным планом студент должен в семестре выполнить одну контрольную работу , которая охватывает все разделы семестра , промежуточная аттестация в виде экзамена. Для проведения промежуточной аттестации по дисциплине математика составлены экзаменационные тесты , которые охватывают раздел материала за 1 семестр обучения. Экзамен по математике проводится на ПВЭМ. Контрольная работа выполняется в отдельной тетради. Содержание каждого вопроса и условие задачи необходимо переписывать полностью, из задания непосредственно перед ответом. Ответы должны быть полными , конкретными, по существу заданного вопроса. Решение задач должны быть подробно расписаны с пояснением . ответами и выводами. Доказательство теорем должно быть оформлено подробно , выделены разделы : что дано, что доказать , чертеж к теореме и доказательство самой теоремы с пояснением ( т.е. объяснение всех пунктов доказательства ).
РАЗДЕЛ 1 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Студент должен :
Знать:
· Определение действительного числа
· Способы решений линейных уравнений и неравенств
· Способы решений квадратных уравнений и неравенств
Уметь:
· Выполнять арифметические действия на множестве действительных чисел
· Решать линейные и квадратные уравнения
· Решать линейные и квадратные неравенства
· Решать системы линейных уравнений и неравенств
· Решать простейшие иррациональные уравнения
РАЗДЕЛ 2 ТРИГОНОМЕТРИЧЕСКИЕ ВЫРАЖЕНИЯ
Студент должен :
Знать:
· определение радиана, формулы перевода градусной меры угла в радианную и обратно; определение синуса, косинуса, тангенса и котангенса числа; основные формулы тригонометрии; свойства и графики тригонометрических функций; понятия обратных тригонометрических функций; способы решения простейших тригонометрических уравнений и неравенств.
Уметь :
· вычислять значения тригонометрических функций с заданной степенью точности; преобразовывать тригонометрические выражения, используя тригонометрические формулы; строить графики тригонометрических функций и на них иллюстрировать свойства функции;
· применять геометрические преобразования (сдвиг и деформацию) при построении графиков; решать простейшие тригонометрические уравнения и неравенства, а также несложные уравнения, сводящиеся к простейшим с помощью тригонометрических формул.
РАЗДЕЛ 3 ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Студент должен :
Знать:
· определение радиана, формулы перевода градусной меры угла в радианную и обратно; определение синуса, косинуса, тангенса и котангенса числа; основные формулы тригонометрии; свойства и графики тригонометрических функций; понятия обратных тригонометрических функций; способы решения простейших тригонометрических уравнений и неравенств.
Уметь :
· вычислять значения тригонометрических функций с заданной степенью точности; преобразовывать тригонометрические выражения, используя тригонометрические формулы; строить графики тригонометрических функций и на них иллюстрировать свойства функции;
· применять геометрические преобразования (сдвиг и деформацию) при построении графиков; решать простейшие тригонометрические уравнения и неравенства, а также несложные уравнения, сводящиеся к простейшим с помощью тригонометрических формул.
РАЗДЕЛ 4 ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Студент должен :
Знать:
· понятия обратных тригонометрических функций; способы решения простейших тригонометрических уравнений и неравенств
Уметь :
· решать простейшие тригонометрические уравнения и неравенства, а также несложные уравнения, сводящиеся к простейшим с помощью тригонометрических формул.
РАЗДЕЛ 5 ПОКАЗАТЕЛЬНАЯ,ЛОГАРИФМИТИЧЕСКАЯ И СТЕПЕННАЯ ФУНКЦИИ
Студент должен :
Знать:
· понятие степени с действительным показателем и ее свойства; определение логарифма числа, свойства логарифмов; свойства и графики показательной, логарифмической и степенной функции; способы решения простейших показательных и логарифмических уравнений и неравенств;
Уметь :
· строить графики показательных, логарифмических функций при различных основаниях и на них иллюстрировать свойства функций; преобразовывать эти графики путем сдвига и деформации; вычислять значения показательных и логарифмических выражений с помощью основных тождеств
РАЗДЕЛ 6 АКСИОМЫ СТЕРЕОМЕТРИИ И ИХ ПРОСТЕЙШИЕ СВОЙСТВА
Студент должен :
Знать :
· основные понятия стереометрии; аксиомы стереометрии и следствия из них
Уметь :
· в ходе решения задач проводить доказательные рассуждения , ссылаясь на аксиомы
РАЗДЕЛ 7 ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Студент должен :
Знать :
· взаимное расположение прямых, прямой и плоскости, двух плоскостей в пространстве; основные теоремы о параллельности прямой к плоскости, параллельности двух плоскостей; свойства параллельного проектирования и их применение для изображения фигур в стереометрии;
Уметь :
· устанавливать в пространстве параллельность прямых, прямой и плоскости, двух плоскостей, используя признаки и основные теоремы о параллельности;
РАЗДЕЛ 8 ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ В ПРОСТРАНСТВЕ
Студент должен :
Знать :
· понятие угла между прямыми, угла между прямой и плоскостью, двугранного угла, угла между плоскостями; основные теоремы о перпендикулярности прямой и плоскости, перпендикулярности двух плоскостей;
Уметь :
· применять признак перпендикулярности прямой и плоскости,
· теорему о трех перпендикулярах, признак перпендикулярности плоскостей для вычисления углов и расстояний в пространстве.
РАЗДЕЛ 9 ПРОИЗВОДНАЯ ФУНКЦИЯ В ТОЧКЕ
Студент должен :
Знать :
· определение производной, ее геометрический и механический смысл; правила и формулы дифференцирования функции; определение дифференциала функции; определение второй производной, ее физический смысл;
Уметь :
· дифференцировать функции, использую таблицу производных и правила дифференцирования, находить производные сложных функций вида
f
(
ax
+
b
); вычислять значения производной функции в указанной точке
РАЗДЕЛ 10 ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ
Студент должен :
Знать:
· определение второй производной, ее физический смысл; достаточные признаки возрастания и убывания функции, существования экстремума; общую схему построения графиков функций с помощью производной; правило нахождения наибольшего и наименьшего значения функции на промежутке;
Уметь:
· находить угловой коэффициент и угол наклона касательной, составлять уравнение касательной к графику функции в данной точке; находить скорость изменения функции в точке; применять производную для исследования реальных физических процессов (нахождение скорости неравномерного движения, угловой скорости, силы переменного тока, линейной плотности неоднородного стержня и т.д.); находить производные второго порядка,
РАЗДЕЛ 11 ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Студент должен :
Знать:
· определение первообразной; определение неопределенного интеграла и его свойства; формулы интегрирования; способы вычисления неопределенного интеграла; определение определенного интеграла, его геометрический смысл и свойства; способы вычисления определенного интеграла; понятие криволинейной трапеции, способы вычисления площадей криволинейных трапеций с помощью определенного интеграла;
Уметь:
· находить неопределенные интегралы, сводящиеся к табличным с помощью основных свойств и простейших преобразований; выделять первообразную, удовлетворяющую заданным начальным условиям; восстанавливать закон движения по заданной скорости, скорость по ускорению, количество электричества по силе тока и т.д.;
РАЗДЕЛ 12 ДЕКАРТОВЫ
КООРДИНАТЫ
В ПРОСТРАНСТВЕ
Студент должен :
Знать :
· понятие декартовых координат в пространстве, понятие вектора , действие над векторами;
Уметь :
· выполнять действия над векторами
РАЗДЕЛ 13 МНОГОГРАННИКИ, ОБЪЕМ МНОГОГРАННИКОВ
Студент должен
Знать :
· понятие многогранника, его поверхности, понятие правильного многогранника; определения призмы, параллелепипеда; виды призм; определения пирамиды, правильной пирамиды; понятие тела вращения и поверхности вращения; определения цилиндра, конуса, шара, сферы; свойства геометрических тел;
Уметь :
· вычислять и изображать основные элементы прямых призм, пирамид, прямых круговых цилиндра и конуса, шара; строить простейшие сечения многогранников и круглых тел; вычислять площади этих сечений.
РАЗДЕЛ 14 ТЕЛА ВРАЩЕНИЯ, ПЛОЩАДИ ПОВЕРХНОСТИ ТЕЛ ВРАЩЕНИЯ , ОБЪЕМ ТЕЛ ВРАЩЕНИЯ
Студент должен :
Знать :
· понятие тел вращения и поверхности вращения; определения цилиндра , конуса , шара , сферы; свойства геометрических тел ;понятие объема и площади поверхности геометрического тела ; формулы для вычисления объемов и площадей поверхностей геометрических тел ;
Уметь :
· вычислять и изображать основные элементы прямых круговых цилиндров и конусов , шара ; строить простейшие сечения круглых тел; вычислять площади; находить объем прямого кругового цилиндра и конуса , шара
Контрольные задания
Домашней контрольной работы
(для первой экзаменационной сессии)
ВАРИАНТ 1
1.Что такое стереометрия .Сформулируйте аксиомы стереометрии.
2.Докажите , что через прямую и не лежащую на ней точку можно провести плоскость , и притом только одну.
3.Какие прямые в пространстве называются параллельными?
4.Какие прямые называются скрещивающимися ?
5.Докажите признак параллельности прямых.
6.Свойства и графики тригонометрических функций.
7.Корень п-ой степени , его свойства.
8.Решите уравнения :
· 2sin x + 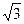 = 0 = 0
· sin 2x =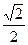
· 3х
– 3х+3
= - 78
· 5х
* 2х =
0,1-3
· 0,3х
* 3х
= 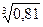
· log x
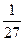 = - 3 = - 3
· log 0.1
( x2
+4x -20 ) = 0
9. Решите неравенство :
· log 0.6
( 6x – x2
) 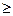 log 0.6
( -8 –x ) log 0.6
( -8 –x )
· log 2.5
( 6 – x ) 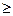 log 2.5
( 4- 3x ) log 2.5
( 4- 3x )
ВАРИАНТ 2
1.Докажите , что через точку вне данной прямой можно провести прямую , параллельную этой прямой , и притом только одну.
2. .Что такое стереометрия .Сформулируйте аксиомы стереометрии.
3.Докажите , что через три точки , не лежащие на одной прямой , можно провести плоскость , и притом только одну.
4.Что значит : прямая и плоскость параллельны ?
5.Докажите признак параллельности прямых.
6.Степень с рациональным и действительным показателем.
7.Понятие синуса, косинуса , тангенса произвольного угла.
8. Решите уравнения :
· 2 cos x -1 = 0
· cos 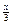 = - = - 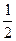
· 0,1х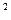 -0,5
* -0,5
* 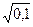 = 0,001 = 0,001
· 52х-1
-52х-3
= 4,8
· log4
5x = log4
35 - log4 7
· log 7
( x2
-12x +36 ) = 0
· log 0.3
( -x2
+ 5x +7 ) = log 0.3
( 10x -7 )
9. Решите неравенство :
· log 2
( 5x – 9 ) 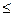 log 2
( 3x + 1 ) log 2
( 3x + 1 )
· log 3
( x2
+6 )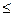 log 3
5x log 3
5x
ВАРИАНТ 3
1.Докажите признак параллельности прямой и плоскости.
2.Какие плоскости называются параллельными ?
3.Докажите признак параллельности плоскостей.
4. Что такое стереометрия .Сформулируйте аксиомы стереометрии.
5.Перечислите свойства параллельного проектирования.
6.Понятие логарифмической функции, свойства , графики.
7.Действительные числа, действия над множеством действительных чисел.
8. Решите уравнения :
· 2 sin x + 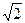 = 0 = 0
· sin 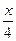 = = 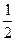
· 0,3х
* 3х
= 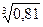
· 2 *( 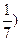 3х+7
– 7* ( 3х+7
– 7* ( 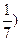 3х+8
= 49 3х+8
= 49
· log4
5x = log4
35 - log4 7
· log 2
( x2
+7x -5 ) = log 2
( 4x -1 )
9. Решите неравенство :
· log 0.6
( 6x – x2
) 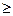 log 0.6
( -8 –x ) log 0.6
( -8 –x )
· log 2.5
( 6 – x ) 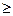 log 2.5
( 4- 3x ) log 2.5
( 4- 3x )
ВАРИАНТ 4
1. Какие прямые в пространстве называются параллельными?
2. .Какие прямые называются скрещивающимися ?
3.Докажите признак параллельности прямых.
4.Докажите , что через точку вне данной плоскости можно провести плоскость , параллельную данной , и притом только одну.
5.Докажите , что если прямые АВ и СД скрещивающиеся , то прямые АС и ВД тоже скрещивающиеся.
6.Понятие показательной функции, свойства , график.
7.Целые и рациональные числа.
8. Решите уравнения :
· sin (-2x ) = 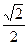
· 3sin2
x – 5sin x-2 =0
· 3х
– 3х+3
= - 78
· 5х
* 2х =
0,1-3
· log2
3x = log2
4 +log2
6
· log 12
( x2
-8x + 16 ) = 0
· log 0.3
( -x2
+ 5x +7 ) = log 0.3
( 10x -7 )
9. Решите неравенство :
· log 2
( 5x – 9 ) 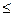 log 2
( 3x + 1 ) log 2
( 3x + 1 )
· log 3
( x2
+6 )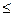 log 3
5x log 3
5x
ВАРИАНТ 5
1.Докажите , что если две параллельные плоскости пересекаются третьей , то прямые пересечения параллельны.
2. Какие прямые в пространстве называются параллельными?
3. Что значит : прямая и плоскость параллельны ?
4. Докажите признак параллельности прямой и плоскости.
5.Докажите ,что все прямые , пересекающие две данные параллельные прямые , лежат в одной плоскости.
6.Основные формулы тригонометрии. Формулы двойного аргумента.
7.Свойства и графики тригонометрических функций.
8. Решите уравнения :
· tg ( -4x ) = 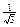
· 3 sin 2
2x +10 sin 2x+3 =0
· 0,1х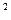 -0,5
* -0,5
* 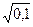 = 0,001 = 0,001
· 52х-1
-52х-3
= 4,8
· 0,3х
* 3х
= 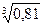
· log x
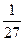 = - 3 = - 3
· log 0.3
( -x2
+ 5x +7 ) = log 0.3
( 10x -7 )
9. Решите неравенство :
· log 0.6
( 6x – x2
) 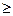 log 0.6
( -8 –x ) log 0.6
( -8 –x )
· log 2.5
( 6 – x ) 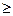 log 2.5
( 4- 3x ) log 2.5
( 4- 3x )
ВАРИАНТ 6
1. Какие прямые называются скрещивающимися ?
2. Докажите признак параллельности плоскостей.
3. Что такое стереометрия .Сформулируйте аксиомы стереометрии.
4. Докажите , что если прямые АВ и СД скрещивающиеся , то прямые АС и ВД тоже скрещивающиеся.
5. Перечислите свойства параллельного проектирования.
6.Определения обратных тригонометрических функций.
7.Формулы сложения и следствия из них.
8. Решите уравнения :
· cos ( -2x) = 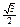
· 4 sin 2
x +11sin x -3 = 0
· 0,3х
* 3х
= 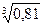
· 2 *( 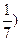 3х+7
– 7* ( 3х+7
– 7* ( 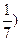 3х+8
= 49 3х+8
= 49
· log2
3x = log2
4 +log2
6
· log 0.3
( -x2
+ 5x +7 ) = log 0.3
( 10x -7 )
9. Решите неравенство :
· log 2
( 5x – 9 ) 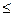 log 2
( 3x + 1 ) log 2
( 3x + 1 )
· log 3
( x2
+6 )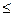 log 3
5x log 3
5x
ВАРИАНТ 7
1.Точки А, В, С, и Д не лежат в одной плоскости. Докажите , что прямые АВ и СД не пересекаются.
2.Точки А. В. С лежат в каждой из двух различных плоскостей . Докажите , что точки лежат на одной прямой.
3. Какие прямые называются скрещивающимися ?
4. Что значит : прямая и плоскость параллельны ?
5. Докажите признак параллельности прямой и плоскости.
6.Тригонометрические функции числового аргумента.
7.Свойства тригонометрических функций числового аргумента и их графики.
8. Решите уравнения :
· 6cos 2
x + cos x -1 =0
· ctg ( - 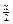 ) = 1 ) = 1
· 32х
-6 * 3х
– 27 = 0
· 0,44-5х
= 0,16 * 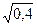
· log4
5x = log4
35 - log4 7
· log 12
( x2
-8x + 16 ) = 0
· log 0.3
( -x2
+ 5x +7 ) = log 0.3
( 10x -7 )
9. Решите неравенство :
· log 0.6
( 6x – x2
) 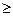 log 0.6
( -8 –x ) log 0.6
( -8 –x )
· log 2.5
( 6 – x ) 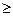 log 2.5
( 4- 3x ) log 2.5
( 4- 3x )
ВАРИАНТ 8
1. Докажите ,что все прямые , пересекающие две данные параллельные прямые , лежат в одной плоскости.
2. Докажите , что если прямые АВ и СД скрещивающиеся , то прямые АС и ВД тоже скрещивающиеся.
3. Перечислите свойства параллельного проектирования.
4. Какие прямые называются скрещивающимися ?
5. Докажите признак параллельности плоскостей.
6.Соотношения между тригонометрическими функциями одного аргумента.
7.Формулы приведения.
8. Решите уравнения :
· 2 cos 2
x – cos x -3 =0
· 2 sin x – 1 =0
· 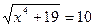
· 2 *( 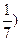 3х+7
– 7* ( 3х+7
– 7* ( 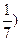 3х+8
= 49 3х+8
= 49
· log4
5x = log4
35 - log4 7
· log 7
( x2
-12x +36 ) = 0
· log 2
( x2
+7x -5 ) = log 2
( 4x -1 )
9. Решите неравенство :
· log 2
( 5x – 9 ) 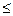 log 2
( 3x + 1 ) log 2
( 3x + 1 )
· log 3
( x2
+6 )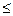 log 3
5x log 3
5x
ВАРИАНТ 9
1. Докажите признак параллельности плоскостей.
2. Что такое стереометрия .Сформулируйте аксиомы стереометрии.
3. Что значит : прямая и плоскость параллельны ?
4. Точки А, В, С, и Д не лежат в одной плоскости. Докажите , что прямые АВ и СД не пересекаются.
5.Докажите признак параллельности прямых.
6.Формулы сложения и следствия из них ( докажите одну из них ).
7.Понятие обратных тригонометрических функций.
8. Решите уравнения :
· 2cos 2
3x -5 cos 3x – 3 =0
· ctg ( - 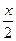 ) = 1 ) = 1
· 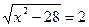
· 2 *( 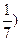 3х+7
– 7* ( 3х+7
– 7* ( 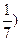 3х+8
= 49 3х+8
= 49
· 0,3х
* 3х
= 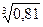
· log4
5x = log4
35 - log4 7
· log 7
( x2
-12x +36 ) = 0
· log 0.3
( -x2
+ 5x +7 ) = log 0.3
( 10x -7 )
9. Решите неравенство :
· log 0.6
( 6x – x2
) 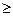 log 0.6
( -8 –x ) log 0.6
( -8 –x )
· log 2.5
( 6 – x ) 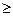 log 2.5
( 4- 3x ) log 2.5
( 4- 3x )
ВАРИАНТ 10
1. Докажите признак параллельности прямых.
2. Докажите признак параллельности плоскостей.
3. Точки А, В, С, и Д не лежат в одной плоскости. Докажите , что прямые АВ и СД не пересекаются.
4. Докажите , что через три точки , не лежащие на одной прямой , можно провести плоскость , и притом только одну.
5. Какие прямые называются скрещивающимися ?
6.Радианное измерение углов
7.Понятие синуса ,косинуса ,тангенса произвольного угла.
8. Решите уравнения :
· 2 sin 2
x + 3 cos x = 0
· 3 tg 2
x + 2 tg x – 1 =0
· 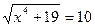
· 32х
-6 * 3х
– 27 = 0
· 0,44-5х
= 0,16 * 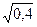
· log4
5x = log4
35 - log4 7
· log 0.1
( x2
+4x -20 ) = 0
9. Решите неравенство :
· log 2
( 5x – 9 ) 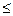 log 2
( 3x + 1 ) log 2
( 3x + 1 )
· log 3
( x2
+6 )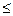 log 3
5x log 3
5x
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Раздел 1 Действительные числа.
Первые представления о числе приобретены людьми в незапамятной древности. Они возникли из счета людей , животных , плодов ,различных изделий человека и других предметов. Эти числа называются теперь натуральными , а в арифметике их называют целыми числами.
В результате выполнения арифметических действий появились дробные числа , затем иррациональные числа , отрицательные числа и комплексные числа , позднее к ним присоединился нуль. Все эти числа вместе образуют множество действительных чисел.
Над множеством действительных чисел производятся следующие операции (действия ): сложение , вычитание ,умножение , деление , возведение в степень ,вычисление значений корня. Выполняя действия мы не забываем , что действия первой ступени ( деление ,умножение, возведение в степень, вычисление корня ) выполняются первыми , а затем действия второй ступени ( сложение и вычитание ).
Обыкновенной дробью называется часть единицы или несколько равных частей единицы. Число , показывающее , на сколько долей разделена единица , называется знаменателем дроби ; число, показывающее количество взятых долей ,- числитель дроби. Если числитель меньше знаменателя, то дробь называется правильной : 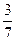 - правильная дробь. Если числитель больше знаменателя , то дробь называется неправильной : - правильная дробь. Если числитель больше знаменателя , то дробь называется неправильной : 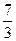 - неправильная дробь. Число , содержащее целую и дробную часть ( например 9 - неправильная дробь. Число , содержащее целую и дробную часть ( например 9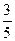 , называется смешанным. , называется смешанным.
Вычисления с обыкновенными дробями иногда становятся громоздкими, если их знаменатели достаточно велики. Поэтому в древности пришли к мысли выбирать не произвольно , а систематически доли единицы. Так пришли к понятию десятичной дроби, над множеством которой производятся все основные операции.
Раздел 2 Тригонометрические выражения.
Угол в 1 радиан
– это такой центральный угол, длина дуги которого равна радиусу окружности. Радианная и градусная меры связаны зависимостью 180 0
= 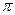 радиан ; угол в п0
равен радиан ; угол в п0
равен 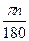 радиан. радиан.
Если в прямоугольном треугольнике , один из острых углов обозначить через 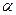 ,катеты соответственно а
и в
, гипотенузу через с
, то отношение а
: с
есть синус острого угла (отношение противолежащего угла катета к гипотенузе) ; отношение в
: с
есть косинус острого угла ( отношение прилежащего катета угла к гипотенузе ) ; отношение а
: в
есть тангенс острого угла ( отношение противолежащего катета угла к прилежащему катету ). ,катеты соответственно а
и в
, гипотенузу через с
, то отношение а
: с
есть синус острого угла (отношение противолежащего угла катета к гипотенузе) ; отношение в
: с
есть косинус острого угла ( отношение прилежащего катета угла к гипотенузе ) ; отношение а
: в
есть тангенс острого угла ( отношение противолежащего катета угла к прилежащему катету ).
Из определений синуса ,косинуса, тангенса, котангенса следуют основные формулы тригонометрии :
Sin 2
x + Cos2
x = 1 tg x * ctg x =1
tg 2
x +1 = 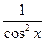 ctg2
x + 1 = ctg2
x + 1 = 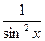
tg x = 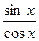 ctg x = ctg x = 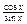
Основой для вывода остальных формул являются формулы сложения :
Cos (a –b) =cos a*cos b + sin a *sin b
Cos (a+ b) =cos a * cos b – sin a * sin b
Sin ( a+ b ) = sin a * cos b +cos a * sin b
Sin ( a –b ) = sin a * cos b – cos a * sin b
tg ( a + b ) =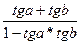
tg ( a – b) =
Из формул сложения путем вывода получаем формулы приведения, формулы суммы и разности синусов и косинусов, формулы двойного аргумента, формулы половинного аргумента.
Для запоминания формул приведения удобно пользоваться мнемоническим правилом :
· перед приведенной функцией ставится тот знак , который имеет исходная функция, если 0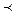 а а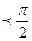 ; ;
· если функция меняется на «кофункцию» ,если п нечетно ; функция не меняется, если п четно.( Кофункциями синуса, косинуса, тангенса, котангенса называются соответственно косинус , синус, котангенс , тангенс.)
Ответьте на контрольные вопросы:
1.Запишите формулы приведения ,
формулы суммы и разности синусов и косинусов, формулы двойного аргумента, формулы половинного аргумента.
2.Запишите знаки тригонометрических функций по четвертям.
3.Выразите в радианную меру величины углов :
· 450
; 36 0
; 1800
; 1500
; 3100
; 360 0
; 720
; 270 0
РАЗДЕЛ 3 .ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Мы считаем , что все углы измерены в радианной мере , и поэтому обозначение рад.
, как правило , опускается. Договорившись считать единицу измерения углов ( 1 радиан ) фиксированной , определяем , тригонометрические функции тригонометрического аргумента.
ОПРЕДЕЛЕНИЕ
:
Числовые функции , заданные формулами у = sin x и у = cos x называются соответственно синусом
и косинусом
( и обозначаются sin . cos )
ОПРЕДЕЛЕНИЕ
:
Числовые функции, заданные формулами у = tg x и у = ctg x , называются соответственно тангенсом
и котангенсом
( и обозначаются tg x и ctg x)
На основании теоремы (о корне) и свойств монотонности тригонометрических функций определены понятия обратных тригонометрических функций.
ОПРЕДЕЛЕНИЕ :
Арксинусом числа а
называется такое число из отрезка 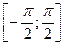 , синус которого равен а. , синус которого равен а.
ОПРЕДЕЛЕНИЕ
: Арккосинусом числа а
называется такое число из отрезка 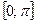 , косинус которого равен числу а
. , косинус которого равен числу а
.
ОПРЕДЕЛЕНИЕ
: Арктангенсом числа а
называется такое число из промежутка 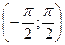 тангенс которого равен числу а
. тангенс которого равен числу а
.
ОПРЕДЕЛЕНИЕ
:Арккотангенсом числа а
называется такое число их отрезка 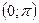 котангенс которого равен числу а
. котангенс которого равен числу а
.
ПРИМЕР
: вычислите значения обратных тригонометрических функций
· arcsin 1 = 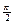 , так как sin , так как sin 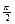 =1 =1
· arcos  , так как cos , так как cos 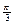 = =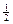
· arcos(-0.5)+arcsin ( -0.5) = 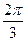 - -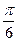 = =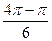 = =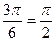
· 2arcsin( -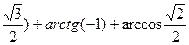 = 2(- = 2(- 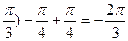
· arcsin(-1)-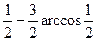 +3arccos(- +3arccos(-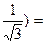 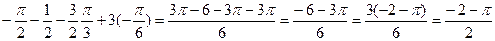
Выполните упражнение самостоятельно :
1.Вычислите :
· arctg(-
· 3arcsin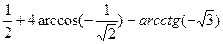
· arctg(-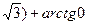
· arccos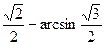
РАЗДЕЛ 4 ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Решение простейших тригонометрических уравнений.
ОПРЕДЕЛЕНИЕ :
Уравнения вида cos x =a sin x =a tg x = a ctg x = a называются простейшими тригонометрическими , при условии а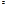 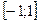 уравнения sin x = a . cos x = a имеют корень, два других уравнения имеют корень при любом а. уравнения sin x = a . cos x = a имеют корень, два других уравнения имеют корень при любом а.
Для решения тригонометрических уравнений существуют формулы корней.
| №
|
Вид уравнения
|
Формулы корней простейших тригонометрических уравнений
|
| 1
|
sin x = a
|
X=(-1)n
arcsin a +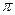 n , n n , n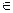 R R
|
| 2
|
cos x = a
|
X = -+
arсcos a +2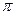 n , n n , n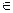 R R
|
| 3
|
tg x = a
|
X = arctg a + 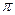 n , n n , n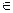 R R
|
| 4
|
ctg x = a
|
X = arcctg a +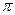 n , n n , n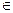 R R
|
1.Решить тригонометрические уравнения : ( образец )
а) cos x = -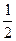
x = -+
arcos (-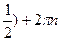 .n .n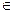 R R
x = -+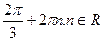
b)
cos 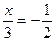
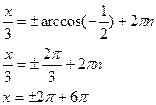 n n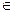 R R
2.Решите уравнения : ( самостоятельно )
· cos x= 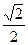
· 2 cos x + = 0
· 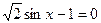
· Sin 2x =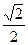
· 2 cos (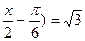
· 2sin2
x+ sin x -1 = 0
· 2 cos 2
x + sin x + 1 =0
При решении тригонометрических уравнений нужно знать определение обратных тригонометрических функций , знать формулы корней простейших тригонометрических уравнений ,уметь пользоваться таблицей элементарных значений тригонометрических функций.
РАЗДЕЛ 5 ПОКАЗАТЕЛЬНАЯ,ЛОГАРИФМИТИЧЕСКАЯ И СТЕПЕННАЯ ФУНКЦИИ
ОПРЕДЕЛЕНИЕ:
функция , заданная формулой У= ах
( где а > 0, а≠1) ,называется показательной функцией с основанием а.
ОПРЕДЕЛЕНИЕ
:Логарифмом числа в
по основанию а
называется показатель , в которую нужно возвести основание а ,
чтобы получить число в.
ОПРЕДЕЛЕНИЕ
:Функция ,заданную формулой У = Logx
a , называется логарифмической функцией с основанием а
.
Сформулируем основные свойства показательной функции ( их доказательство выходит за рамки общеобразовательной подготовки )
1.Область определения показательной функции есть множество всех действительных чисел.
2.Область значения показательной функции есть множество всех положительных действительных чисел.
3.При любых действительных значениях Х и У справедливы равенства :
· ах
ау
= ах+у
· 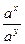 =ах-у =ах-у
· (ав )х
=ах
вх
· (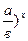 = = 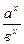
· (ах
)у
= аху
Решение простейших показательных , логарифмических уравнений и неравенств.
При решении простейших показательных уравнений используется определение показательной функции и ее основные свойства.
Решим уравнение :
1. 7х-2
=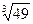
Приведем основание показательной функции правой части уравнения к числу 7, в результате преобразований получаем 7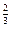 , данное уравнение после преобразований имеет вид 7х-2
= 7 , данное уравнение после преобразований имеет вид 7х-2
= 7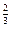 , на основании свойства показательной функции имеем , что х-2 = , на основании свойства показательной функции имеем , что х-2 = 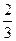 , следовательно х = 2 , следовательно х = 2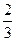 . .
2. 5х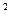 -2х-1
=25 -2х-1
=25
Перепишем его в виде 5х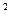 -2х-1
= 52
на основании свойства показательной функции имеем , что х2
-2х-1 = 2. Приходим к квадратному уравнению , решаем его и получаем два действительных корня х =3 и х= -1 , следовательно корнями показательного уравнения являются числа 3 и -1. -2х-1
= 52
на основании свойства показательной функции имеем , что х2
-2х-1 = 2. Приходим к квадратному уравнению , решаем его и получаем два действительных корня х =3 и х= -1 , следовательно корнями показательного уравнения являются числа 3 и -1.
При решении простейших логарифмических уравнений используются определения логарифма числа , понятие логарифмической функции , ее области определения и основные свойства логарифмической функции .
Решим уравнение
:
1. Log 2
(x2
+4x+3 ) =3
По определению логарифма числа имеем х2
+4х+3 = 23
, получаем , что х2
+4х+3 = 8 , или х2
+4х +3 -8 = 0 , приводим подобные , получаем квадратное уравнение , решаем его и получаем два два действительных корня х =1 , х = -5 , следовательно корни логарифмического уравнения числа 1 и -5 .
2. Log (2x+3)=Log(x+1)
По свойству логарифмической функции имеем , что 2х+3=х+1 , решаем линейное уравнение и получаем , что х = -2 , которое не обращает данное уравнение в верное равенство.
При решении показательных неравенств используется понятие показательной функции . свойство монотонности показательной функции, свойства линейных неравенств и алгоритм их решения.
Решим неравенство
:
1. 0,57-3х
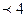 , представим основание показательной функции в правой части неравенства в виде числа 0,5-2
, перепишем неравенство с новым основанием , представим основание показательной функции в правой части неравенства в виде числа 0,5-2
, перепишем неравенство с новым основанием
0,5 7-3х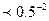 , исходя из того , что основание показательной функции число равное 0,5 следовательно показательная функция убывающая и это значит , что 7-3х
, исходя из того , что основание показательной функции число равное 0,5 следовательно показательная функция убывающая и это значит , что 7-3х 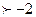 решаем неравенство первой степени и получаем , что -3х решаем неравенство первой степени и получаем , что -3х 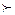 -9 и х -9 и х 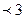 .Значит множество ( - .Значит множество ( - 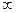 ; 3 ) есть решением данного неравенства. ; 3 ) есть решением данного неравенства.
2. Решим неравенство :
6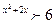 2
при данном основании а =6 показательная функция возрастает ,а это значит, что х2
+2х 2
при данном основании а =6 показательная функция возрастает ,а это значит, что х2
+2х 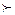 2 или х2
+2х -2 2 или х2
+2х -2 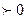 решая неравенство 2 степени , вычисляя нули функции получаем х =- 3 и х = 1, а это значит множество чисел ( - решая неравенство 2 степени , вычисляя нули функции получаем х =- 3 и х = 1, а это значит множество чисел ( -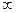 ; -3 ) и ( 1; ; -3 ) и ( 1; 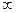 ) есть решение данного неравенства. ) есть решение данного неравенства.
При решении логарифмических неравенств всегда используются свойство монотонности функции , свойства линейных неравенств и алгоритм их решения.
3. Решим неравенство :
1.log 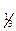 (5-2
x
)
(5-2
x
)
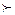 2 число -2 представим в виде логарифма числа -2 = log 1/3
9 .Поэтому данное неравенство можно записать в виде log 1/3
( 5-2x )
2 число -2 представим в виде логарифма числа -2 = log 1/3
9 .Поэтому данное неравенство можно записать в виде log 1/3
( 5-2x ) 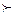 log 1/3
9 .Логарифмическая функция с основанием 1/3 определена и убывает на множестве R+
.Следовательно составляя систему из двух неравенств получаем : 5-2х log 1/3
9 .Логарифмическая функция с основанием 1/3 определена и убывает на множестве R+
.Следовательно составляя систему из двух неравенств получаем : 5-2х 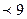 и 5-2х и 5-2х 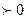 , решаем данную систему и получаем , что х принадлежит множеству ( -2 ; 2,5 ). , решаем данную систему и получаем , что х принадлежит множеству ( -2 ; 2,5 ).
РАЗДЕЛ 6 . Аксиомы и их простейшие следствия.
СТЕРЕОМЕТРИЯ
– это раздел геометрии , в котором изучаются фигуры в пространстве. В стереометрии , так же как и в планиметрии , свойства геометрических фигур устанавливаются путем доказательства соответствующих теорем, При этом отправными являются свойства основных геометрических фигур, выражаемые аксиомами. Основными фигурами в стереометрии являются точка , прямая и плоскость.
Группа аксиом состоит из трех аксиом.
С1
Какова бы ни была плоскость , существуют точки принадлежащие этой плоскости, и точки , не принадлежащие ей.
С2
Если две различные плоскости имеют общую точку , то они пересекаются по прямой , проходящей через эту точку.
С3
Если две различные прямые имеют общую точку , то через них можно провести плоскость , и притом только одну.
Существует группа теорем , которые являются следствиями из аксиом стереометрии.
ТЕОРЕМА15.3 Через прямую и не лежащую на ней точку можно провести плоскость , и при том только одну.
ТЕОРЕМА 15.2 Если две точки прямой принадлежат плоскости , то вся прямая принадлежит этой плоскости .
ТЕОРЕМА 15.3 Через три точки, не лежащие на одной прямой , можно провести плоскость , и притом только одну .
При изучении данного раздела вы должны знать аксиомы стереометрии и уметь доказывать теоремы ( следствия из аксиом стереометрии).
РАЗДЕЛ 7 . ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ.
В пространстве существует несколько видов расположения прямых : пересекающие , параллельные , скрещивающиеся.
ОПРЕДЕЛЕНИЕ :
две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются.
ОПРЕДЕЛЕНИЕ
: прямые , которые не пересекаются и не лежат в одной плоскости , называются скрещивающимися.
Теорема 16.1 доказывает свойства параллельности прямых :
Через точку вне данной прямой можно провести прямую , параллельную этой прямой , и притом одну.
Так же существует признак параллельности прямых .
ТЕОРЕМА 16.2
Две прямые , параллельные третьей прямой , параллельны.
ОПРЕДЕЛЕНИЕ
: прямая и плоскость называются параллельными , если они не пересекаются.
А теорема 16.3 является признаком параллельности прямой и плоскости.
Если прямая, не принадлежащая плоскости , параллельна какой–нибудь прямой в этой плоскости, то она параллельна и самой плоскости.
ОПРЕДЕЛЕНИЕ
: две плоскости называются параллельными , если они не пересекаются.
ТЕОРЕМА 16.4
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости , то эти плоскости параллельны.
На ряду с этим вы должны уметь доказывать теоремы о существовании плоскости , параллельной данной плоскости.
ТЕОРЕМА 16.5
Через точку вне данной плоскости можно провести плоскость , параллельную данной , и притом только одну.
Нужно так же отметить о существовании свойств параллельных плоскостей это следующие утверждения :
Если две параллельные плоскости пересекаются третьей , то прямые пересечения параллельны.
Отрезки параллельных прямых , заключенные между двумя параллельными плоскостями ,равны.
Параллельные отрезки фигуры изображаются на плоскости чертежа параллельными отрезками.
ЛИТЕРАТУРА
Основная
1. Атанасян Л.С. Геометрия (10-11) – М., Просвещение, 1994.
2. Афанасьева О.Н., Бродкий Я.С., Гуткин И.И., Павлов АЛ. Cборник задач по математике для
техникумов. – М.: Наука, 1987.
3. Валуцэ И.И. Математика для техникумов. – М.: Наука, 1990.
4. Колмогоров А. Н. Абрамов А. М. и др. Алгебра и начала анализа (10 – 11) – М., Просвещение, 1995
5. Математика для техникумов. Алгебра и начало анализа./ под ред. Яковлева Г.Н. Ч.1. – М., Наука, 1987.
6. Математика для техникумов. Алгебра и начало анализа./ под ред. Яковлева Г.Н. Ч.2. – М., Наука, 1988.
7. Математика для техникумов. Геометрия./ под ред. Яковлева Г.Н. – М., Наука, 1989.
8. Погорелов А.В. Геометрия (7 – 11) – М. Просвещение, 1997.
9. Подольский В.А. и др. Сборник задач по математике: Учебное пособие для средних специальных учебных заведений /Подольский В.А., Суходольский А.М. и др.– 2-е изд. перераб. и доп. – М.: Высшая школа, 1999.
Дополнительная
1. Афанасьева О.Н., Бродский Я.С. , Павлов А.Л. Математика для техникумов. – М.: Наука, 1991
2. Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних специальных учебных заведений. – М.: Высшая школа, 1997.
1 Упростите выражение 4 sin2
α + 5 – 4cos2
α
1) 1
2) 9
3) 5 + 4cos2α
*4) 5 - 4cos2α
2 Решите неравенство: 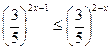
1) [3:+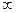 ) )
2) (-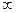 : 1] : 1]
*3) [1 : +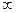 ) )
4) R
3 Найдите корень уравнения 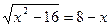
*1) 5
2) 1/3
3) ø
4) -2
4 Решите уравнение tg x = 1
1) 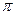 + +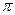 n n
*2) 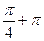 n n
3) ø
4) R
5 Упростите выражение (2а 0,3
) 3
+ 3а 0,9
*1) 11а 0,9
2) 5а 2,7
3) 5а 0,9
4) 11а 2,7
6 Найдите область определения функции у=log2
х2
*1) (-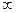 : + : + 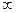 ) )
2) (0: 1)
3) (-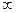 :1) :1)
4 ) (1: +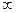 ) )
7 Найдите значение выражения log2
36 – log2
144
1) -4
2) 4
*3) -2
4) 2
8 Найдите значение выражения log1/2
2 + log1/2
16
*1) -5
2) 5
3) 0
4) 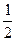
9 Найдите корень уравнения log2
(х-1)=4
*1) 17
2) - 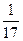 
3) -17
4) ø
10 Найдите значение выражения 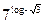
*1) 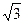
2) 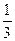
3) 7
4) -7
11 Найдите корень уравнения 2sinх – 1 =0
*1) 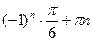
2) 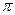 n n
3) 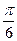
4) 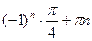
12 Найдите корень уравнения lg(3x-2) = lg4
1) - ½
*2) 2
3) ø
4) R
13 Решите неравенство 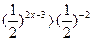
1) R
*2) (-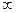 : ½) : ½)
3) ( ½ : +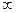 ) )
4) (0 : ½)
14 Формула sin2α
1) sin α ∙ cos α
2) 2sin α
*3) 2sin α ∙ cos α
4) cos2
α
15 Стереометрия –это раздел геометрии, в котором фигуры изучаются на
1) плоскости
2) прямой
*3) пространстве
4) треугольнике
16 Через три точки, не лежащие на одной прямой, можно провести …, и притом только одну
*1) плоскость
2) прямую
3) треугольник
4) окружность
17 Прямые, которые не пересекаются и не лежат в одной плоскости, называются
*1) скрещивающиеся
2) параллельными
3) перпендикулярными
4) пересекающимися
18 Две прямые, параллельные третьей прямой, …
1) равны
*2) параллельны
3) перпендикулярны
4) не пересекаются
19 Упростите выражение 1 – sin2
t
*1) cos2
t
2) sin2t
3) cos2t
4) tg2
t
20 Вычислите 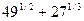
1) 7
*2) 10
3) -10
4) 1/10
21Вычислите log2
24
1) ¼
2) -2
3) 2
*4) 4
22 Найдите значение числового выражения 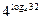
1) -32
*2) 32
4) 4
4) -4
23 Какая из перечисленных функций показательная
*1) 2х
2) х4
3) sin x
4) log2
x
24 Какая функция четная
1) sin x
*2) cos x
3) a x
4) loga
x
25 Упростите выражение 6-6sin 2
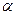 +6cos2 +6cos2
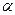
1) 6
2) 12cos2
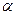
*3) 6+6cos2

4) 0
26 Решите неравенство: 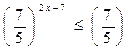 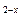 

1)[3:+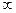 ) )
*2)(- 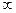 :+3] :+3]
3)[9:+ 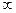 ) )
4)R
27 Найдите корень уравнения: 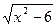 =3-х =3-х
*1) 2,5
2) -2,5
3) ø
4) 2
28 Решите уравнение:ctg x=1
*1)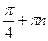
2) 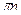
3) ø
4) - 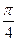 + +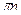
29 Найдите значения выражения : в 2,5
: в -0,5
при в=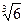
1)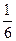
2) 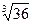
3) 36
*4) 6
30 Найдите область определения функции у=log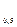 (х-1) (х-1)
1) R
*2) 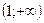
3) (-2;3)
4)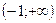
31 Найдите значения выражения 5sin2
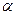 +2,2-5cos2 +2,2-5cos2
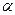 .если10 sin2 .если10 sin2
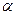 =3 =3
1) 4
2) 3
3) 2,8
*4) 0,2
32 Найдите значения выражения : log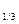 3+ log 3+ log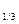 27 27
*1) – 4
2) 4
3) 1/4
4) -1/4
33 Найдите корень уравнения log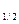 (х-2)= -4 (х-2)= -4
*1) 18
2) –18
3) 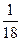
4) ø
34 Найдите значение выражения 9 log
9 log
9
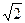
*1) 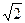
2) 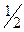
3) 9
5) –9
35 Найдите корень уравнения 2cos х-1=0
*1)  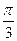 +2 +2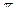 n n
2) 2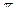 n n 
3) ø
5) (-1)n
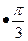 + +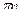
36 Найдите корень уравнения lg(3х-2)=1
*1) 4
2) -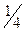
3) -4
4) ø
37 Решите неравенство 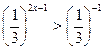
1) 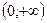
2) 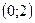
*3) 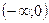
4) R
38 Формула cos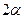 , есть выражение , есть выражение
*1) 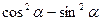
2) 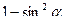
3) 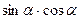
4) 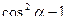
39 Через прямую и не лежащую на ней точку можно провести..., и притом только одну.
1) прямую
2) угол
3) трапецию
*4) плоскость
40 Две прямые в пространстве называются ..., если они лежат в одной плоскости и не пересекаются.
1) перпендикулярными
*2) параллельными
3) пересекающимися
4) скрещивающимися
41 Через точку вне данной прямой можно провести …, параллельную этой прямой, и притом только одну
1) плоскость
2) угол
*3) прямую
4) многоугольник
42 Две прямые называются перпендикулярными если, они пересекаются под углом
1) 180
2) 45
*3) 90
4) 270
43 Упростите выражение 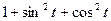
1) 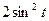
*2) 2
3) 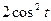
4) -1
44 Вычислите 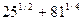
*1) 8
2) 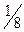
3) 5
4) 3
45 Вычислите 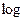 8
8-2 8
8-2
1) -8
2) 8
3) 2
*4) -2
46 Найдите значения числового выражения 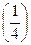 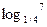
1) -7
*2) 7
3) 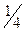
4) -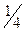
47 Какая из перечисленных функций степенная
1) 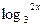
2) 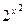
3) sin2х
*4) 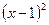
48 Какая функция нечетная
*1) tgх
2) х2
3) х2
+2
4) 2х2
+4
ЭКЗАМЕНАЦИОННЫЙ МАТЕРИАЛ
|