| МИНИСТЕРСТВО ИНДУСТРИИ И НОВЫХ ТЕХНОЛОГИЙ РК
Республиканское государственное предприятие
НАЦИОНАЛЬНЫЙ ЯДЕРНЫЙ ЦЕНТР РК (РГП НЯЦ РК)
Дочернее государственное предприятие
ИНСТИТУТ ЯДЕРНОЙ ФИЗИКИ
(ДГП ИЯФ РГП НЯЦ РК)
УДК 53.043
Красовицкий Павел Михайлович
МОЛЕКУЛЯРНАЯ РЕЗОНАНСНАЯ ДИФФУЗИЯ В ТВЕРДОМ ТЕЛЕ
Работа, представленная на конференцию - конкурс НИОКР
молодых ученых и специалистов
Национального ядерного центра Республики Казахстан
(фундаментальные исследования)
Курчатов 2011
АВТОР
Красовицкий Павел Михайлович
СНС ЛТЯФ
Год рождения - 1976,
образование высшее (КазНУ им. Аль-Фараби, 2002),
специальность – физик,
квалификация по диплому – физик,
работает с 2001 года в Лаборатории теоретической ядерной физики ИЯФ НЯЦ РК,
общий стаж работы -15 лет .
Красовицкий Павел Михайлович.
МОЛЕКУЛЯРНАЯ РЕЗОНАНСНАЯ ДИФФУЗИЯ В ТВЕРДОМ ТЕЛ
Работа, представленная на конференцию - конкурс НИОКР молодых ученых и специалистов Национального ядерного центра Республики Казахстан
Дочернее государственное предприятие «Институт геофизических исследований» Республиканского государственного предприятия «Национальный ядерный центр Республики Казахстан» (ДГП ИГИ РГП НЯЦ РК).
050020, г. Алматы, Чайкина 4, тел. (727)263-13-30, (727)263-48-82,
факс.(727) 263-48-82, E_mail: kcd1234@mail.kz
РЕФЕРАТ
Работа содержит 13 страниц, 5 рисунков, 7 источников.
Актуальность:
Исследования молекулярной резонансной диффузии в твердом теле тесно связано с новейшими направлениями развития науки – исследованиями в области нанотехнологий и наноматериалов. Они прямо касаются процессов, происходящих на малых расстояниях в твердом теле. Эффекты диффузии сильно влияют на происходящие процессы, и знание их помогает находить новые эффекты, особенно в связи с знанием новых эффектов для самого процесса диффузии.
Цель работы:
Получение предварительной оценки для температурного диапазона и параметров потенциалов твердого тела, в котором возможно превышение молекулярной резонансной диффузии над одноатомной.
Задачи исследований:
Получение расчетной модели молекулярной резонансной диффузии
Составление программы и проведение расчетов по полученной модели
Анализ результатов.
Методика исследований:
Создание расчетных блоков и программ в среде Maple и Fortran, анализ результатов на основе общей теории диффузии.
Результат работ:
Зависимость коэффициентов диффузии от ширины и высоты барьера.
Параметры барьеров, при которых возможно превышение молекулярной резонансной диффузии над одночастичной.
Научная новизна:
Впервые исследована простая модель молекулярной резонансной диффузии в твердом теле. Впервые предсказаны основные характеристики явления, такие как зависимость от ширины, линейного размера ямы между двумя барьерами
Личный вклад автора:
Большую часть работы автор сделал самостоятельно. Формализм резонансной прозрачности, некоторые предварительные расчеты были придуманы и проделаны ГНС ЛТЯФ Пеньковым Ф.М, автор приносит ему самую горячую благодарность.
Публикации:
Работы автора опубликованы за пять лет в более чем двадцати научных журналах, в том числе:
Chuluunbaatar O., Gusev A.A., Vinitsky S.I., Derbov V.L., Krassovitskiy. Channeling problem for charged particles produced by confining environment. // Ядерная физика. - 2009. – Т. 72, № 5. –с. 811–821.
С.И., Гусев, А.А.. Чулуунбаатар О., Дербов В.Л., Серов В.В, Красовицкий П.М.. О коэффициенте усиления скорости ядерной реакции в магнитном поле и канале кристалла // Ядерная и радиационная физика: Материалы 7-ой международной конференции, 8-11 сентября 2009, г.: ИЯФ НЯЦ РК, Алматы, 2009, с.58
Ибраева Е.Т., Жусупов М.А., Иммамбеков О., Красовицкий П.М. Интерференционные эффекты в протонном рассеянии на ядре 15
N при промежуточных энергиях // Ядерная физика. - 2010. – Т. 73, № 8. – с. 1497-1504
ПЕРЕЧЕНЬ СОКРАЩЕНИЙ, УСЛОВНЫХ ОБОЗНАЧЕНИЙ, СИМВОЛОВ,
ЕДИНИЦ И ТЕРМИНОВ
∆– оператор Лапласа, в работе 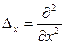 ; ;
Гауссов потенциал – потенциал вида 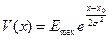 ; σ определяет ширину барьера, а E
max
– его высоту. ; σ определяет ширину барьера, а E
max
– его высоту.
СОДЕРЖАНИЕ
| Введение
Теоретические предпосылки. Модель резонансной диффузии
Расчет в выбранном приближении
Численная схема и результаты расчета
Заключение
Список использованных источников
|
6
7
9
10
12
13
|
Введение
Исследования поведения систем из трех и более частиц дают науке много новых и интересных эффектов. Эти эффекты обычно невозможны в задаче двух тел. В качестве примера можно назвать широко известные эффект Ефимова, теорема Томсона, и т.д.
В 1994 году японские ученые впервые предложили еще один эффект подобного рода [1]. Позднее он был изучен во многих работах [2-5], и был назван «эффектом резонансной прозрачности». Расчеты показывают, что пара одинаковых частиц может проходить одномерный барьер резонансным образом, вероятность прохождения при определенной энергии может достигать единицы. В основе эффекта лежит следующее объяснение: пара связанных частиц может образовывать вблизи барьера квазисвязанные состояния. При совпадении энергии пары частиц с энергией такого состояния и наблюдается прозрачность барьера.
Широкий ряд работ, изучающих резонансную прозрачность [1-5], показывает, что исследования в этой области имеют большое значение и широкое применение. Одной из возможных областей является диффузия в твердом теле. Начало этой работы было дано ранее [6]. Из параметров задачи ясно, что резонансы для двухатомных молекул имеют чрезвычайно малую ширину, что, впрочем, компенсируется большим их количеством. Поэтому эффект резонансной прозрачности невозможно наблюдать напрямую – ширина резонансов гораздо меньше естественного теплового уширения для значений энергии. Однако, указанный эффект может давать вклад в интегральные величины, например, диффузию.
Прямой расчет молекулярной резонансной диффузии, даже для простой модели, требует значительных машинных ресурсов. При этом результат заранее предсказать невозможно. В данной работе представлена простая модель молекулярной диффузии, позволяющая сделать предварительные оценки.
Актуальность:
Исследования молекулярной резонансной диффузии в твердом теле тесно связано с новейшими направлениями развития науки – исследованиями в области нанотехнологий и наноматериалов. Они прямо касаются процессов, происходящих на малых расстояниях в твердом теле. Эффекты диффузии сильно влияют на происходящие процессы, и знание их помогает находить новые эффекты, особенно в связи с знанием новых эффектов для самого процесса диффузии.
Цель работы:
Получение предварительной оценки для температурного диапазона и параметров потенциалов твердого тела, в котором возможно превышение молекулярной резонансной диффузии над одноатомной.
Задачи исследований:
Получение расчетной модели молекулярной резонансной диффузии
Составление программы и проведение расчетов по полученной модели
Анализ результатов.
Методика исследований:
Создание расчетных блоков и программ в среде Maple и Fortran, анализ результатов на основе общей теории диффузии.
Результат работ:
Зависимость коэффициентов диффузии от ширины и высоты барьера.
Параметры барьеров, при которых возможно превышение молекулярной резонансной диффузии над одночастичной.
Научная новизна:
Впервые исследована простая модель молекулярной резонансной диффузии в твердом теле. Впервые предсказаны основные характеристики явления, такие как зависимость от ширины, линейного размера ямы между двумя барьерами
Теоретические предпосылки. Модель резонансной диффузии
Эффект резонансной прозрачности описывается в рамках следующего формализма [2]. Две одинаковые частицы с массами 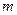 , связанные потенциалом , связанные потенциалом 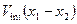 , проходят сквозь барьер, описываемый потенциалом , проходят сквозь барьер, описываемый потенциалом 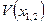 . Их эволюция подчиняется уравнению Шредингера с гамильтонианом: . Их эволюция подчиняется уравнению Шредингера с гамильтонианом:
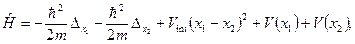
С помощью преобразования координат
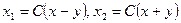 (1) (1)
это уравнение преобразуется к виду
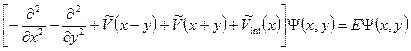 . (2) . (2)
Константа С
выбирается, исходя из вида потенциала, связывающего две частицы. Так, для часто используемого в подобных расчетах осцилляторного потенциала 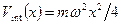 константа константа  . В этом случае . В этом случае 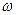 – частота колебаний осциллятора. – частота колебаний осциллятора.
Для этого уравнения решается задача рассеяния, то есть задаются специальные граничные условия для волновой функции. Эти условия имеют вид:
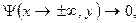
что означает невозможность разрыва связи пары при прохождении барьера, и
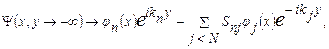 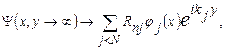
где функции 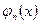 – собственные функции уравнения Шредингера с потенциалом – собственные функции уравнения Шредингера с потенциалом 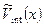 , собственные значения этого уравнения , собственные значения этого уравнения 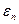 . Коэффициенты S
и R
определяют вероятности прохождения и отражения барьера соответственно: . Коэффициенты S
и R
определяют вероятности прохождения и отражения барьера соответственно:
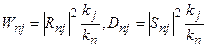
где импульсы 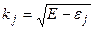 . .
Классические модели диффузии в твердом теле предполагают абсолютную непрозрачность внутрикристаллических барьеров при энергии частицы E
, меньшей высоты барьера E
max
. То есть вероятность прохождения барьера P
для одной частицы пропорциональна единичной функции:
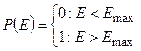
При этом диффузию как функцию энергии можно записать в виде: D=
D
0
P
(E
),
где D
0
имеет масштаб газовой диффузии [7]. После термодинамического усреднения получаем известную формулу эмпирической зависимости диффузии от температуры:
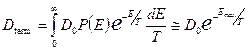 . .
В квантовом случае вероятность P
(E
) нужно заменить на полную вероятность прохождения через барьер: 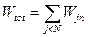 . Соответственно: . Соответственно:
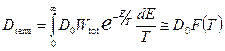 . .
Температура 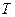 берется в единицах энергии. Пример расчета функции берется в единицах энергии. Пример расчета функции 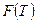 приведен в [6]. Дальнейшие расчеты при данных параметрах показали, что превышения молекулярной резонансной диффузии над одночастичной не наблюдается. приведен в [6]. Дальнейшие расчеты при данных параметрах показали, что превышения молекулярной резонансной диффузии над одночастичной не наблюдается.
Расчеты, пример которых упомянут выше, чрезвычайно сложны и продолжительны. В [6] использовались параметры потенциалов твердого тела «по возможности», то есть такие, с которыми еще могла работать программа, написанная для машины с восьмиразрядным процессором. При этом некоторая часть резонансов уже и здесь не могла быть рассчитана точно, и для учета их вкладов использовалась полуэмпирическая модель экстраполяции от точно просчитанных резонансов. Параметры потенциалов реальных твердых тел задают еще более сложную перспективу для расчетов. Имеет смысл для предварительной оценки целесообразности таких расчетов в использовании неких приближений, которые, конечно, огрубляют искомый результат, но, вместе с тем, могут дать хотя бы предварительную картину.
Уравнение (2) соответствует двумерной задаче рассеяния на потенциальном барьере, примерный вид которого приведен на рис. 1.

Рисунок 1 – Суммарный потенциал в задаче на резонансную диффузию. Случай осцилляторного потенциала взаимодействия частиц и гауссового – барьера. Стрелками указаны метастабильные состояния
Для получения предварительных результатов заменим эту задачу на более простую: одномерное рассеяние на двух прямоугольных барьерах. Основными параметрами будут ширины и высоты барьеров, для масштабирования будут применяться преобразования, аналогичные (1). Коэффициент C
выбран, по аналогии с [6], как для двухатомной молекулы бериллия.
В качестве одного из учитываемых параметров используется также глубина ямы между двумя барьерами. Этот параметр необходимо учитывать, так как в некоторых случаях, например, когда рассматривается рассеяние на двумерном барьере из двух гауссовых потенциалов, резонансное прохождение при низких энергиях отсутствует. В работе исследуется зависимость для задачи, когда потенциал связи частиц выбран осцилляторный, а барьерный потенциал – гауссовой формы. Для этого случая минимальная энергия, при которой возможно резонансное прохождение, определяется как сумма:
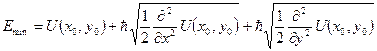 , (3) , (3)
где 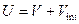 – суммарный потенциал. Точка – суммарный потенциал. Точка 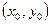 является решением уравнения на поиск минимум потенциальной энергии является решением уравнения на поиск минимум потенциальной энергии
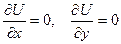 . .
Формула (3) формируется следующим образом: первое слагаемое – значение потенциала в точке минимума, в двух других выражения под корнем – «частота» двух перпендикулярных осцилляторных потенциалов, которыми можно аппроксимировать поведение суммарного потенциала в точке минимума. В целом два последних слагаемых – выражение для минимальной энергии осциллятора 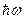 . Этот параметр является достаточно важным – он определяет, кроме вышеуказанного, в спорных случаях возможность резонансной диффузии в целом. Резонансная диффузия возможна, если только (3) меньше высоты барьера. . Этот параметр является достаточно важным – он определяет, кроме вышеуказанного, в спорных случаях возможность резонансной диффузии в целом. Резонансная диффузия возможна, если только (3) меньше высоты барьера.
Расчет в выбранном приближении
При преобразовании из (1) в (2) потенциалы преобразуются следующим образом. Коэффициент преобразования 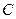 выбирается, чтобы преобразовать потенциал выбирается, чтобы преобразовать потенциал 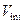 в наиболее простой вид, например, в наиболее простой вид, например, 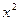 . Предполагая, данный случай за образец, получаем коэффициент преобразования, как было сказано выше, в виде . Предполагая, данный случай за образец, получаем коэффициент преобразования, как было сказано выше, в виде 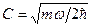 . Можно заметить, что этот параметр имеет размерность длины, то есть, он может быть переписан в виде . Можно заметить, что этот параметр имеет размерность длины, то есть, он может быть переписан в виде 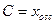 , где , где
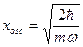 . .
В случае, если, как и в [6], рассматривается молекула бериллия, этот параметр равен 0.16 Å. Потенциал 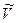 в (2) будет иметь вид в (2) будет иметь вид
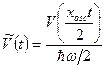 , , 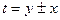 , ,
параметр 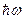 в данном случае равен 400 К [6]. В (1) множитель в данном случае равен 400 К [6]. В (1) множитель 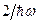 также появиться перед энергией, и в (2) энергия уже будет выражаться в этих единицах. также появиться перед энергией, и в (2) энергия уже будет выражаться в этих единицах.
Задача прохождения атома через тот же барьер, то есть одной частицы с массой 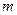 , описывается с помощью уравнения Шредингера , описывается с помощью уравнения Шредингера
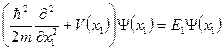 . .
Для корректного сравнения это уравнение преобразуется таким образом, чтобы перед энергией снова появился тот же множитель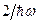 . Очевидно, это возможно, если использовать преобразование . Очевидно, это возможно, если использовать преобразование
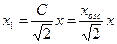 . .
Потенциал, таким образом, будет иметь преобразованный вид:
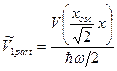 . .
Потенциал для одной частицы, таким образом «тоньше» на 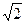 , чем потенциал в (2) для двухчастичной задачи. , чем потенциал в (2) для двухчастичной задачи.
Численная схема и результаты расчетов
Для расчетов использовалась аналитическая формула для вероятности прохождения через два одинаковых прямоугольных барьера 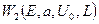 , и аналитическая формула вероятности прохождения одного барьера , и аналитическая формула вероятности прохождения одного барьера 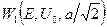 , как функции от энергии. Характерный вид кривой вероятности показан на рис. 2. , как функции от энергии. Характерный вид кривой вероятности показан на рис. 2.
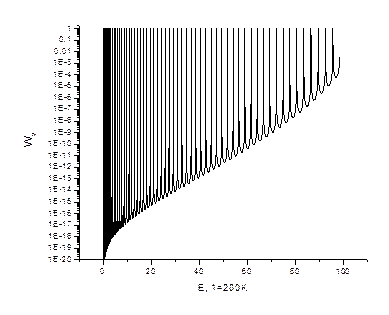
Рисунок 2 – Пример расчета вероятности прохождения двух барьеров. Параметры 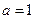 , , 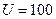 и и 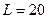
Параметрами были ширина барьера 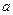 , высота , высота 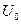 и расстояние между барьерами и расстояние между барьерами 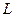 . Обе функции интегрировались вместе с весовой функцией . Обе функции интегрировались вместе с весовой функцией 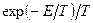 . Интегрирование производилось численно с помощью программы, составленной в программной среде Fortran. . Интегрирование производилось численно с помощью программы, составленной в программной среде Fortran.
На рисунке 3 представлены результаты расчетов для различных значений параметра 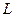 . .
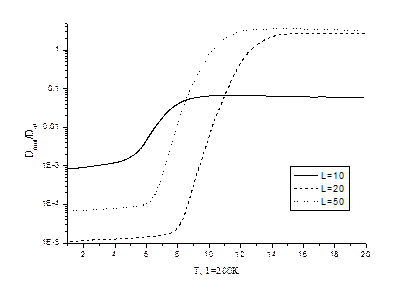
Рисунок 3 – Отношение молекулярной и атомарной диффузии при параметрах 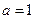 , , 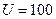 и различных и различных 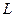
Из рисунка видно, что существует некоторое критическое значение 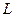 , находящееся между 10 и 20 единицами, выше которого можно наблюдать молекулярную резонансную диффузию, сравнимую по величине с атомарной. При значениях выше этого значения поведение кривой меняется не столь существенно. , находящееся между 10 и 20 единицами, выше которого можно наблюдать молекулярную резонансную диффузию, сравнимую по величине с атомарной. При значениях выше этого значения поведение кривой меняется не столь существенно.
Из наших оценок можно сделать вывод, что значение этого линейного параметра определяется как
(10÷20)·0.16 Å ~ 2 Å
Этот параметр соответствует, правда, достаточно косвенно, линейному размеру ямы между барьерами в двумерном случае. Можно установить, что молекулярная резонансная диффузия будет наблюдаться не при любых параметрах, достаточных для образования метастабильных состояний. Как и в изучаемом одномерном случае, если размеры меньше некоего значения, образованных состояний получается слишком мало, чтобы обеспечить преобладание резонансной диффузии.
На рисунке 4 представлены результаты расчетов при различных значениях 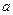 . .
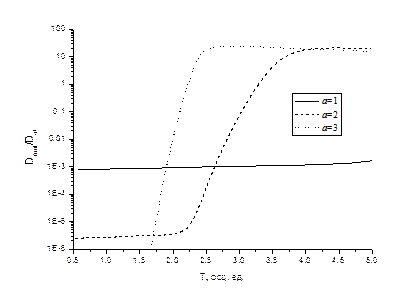
Рисунок 4 - Отношение молекулярной и атомарной диффузии при параметрах 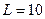 , , 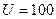 и различных и различных 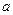
Видно, что даже при недостаточно большом параметре 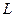 молекулярная резонансная диффузия в значительной мере определяется шириной барьера. Рост ширины барьеров вызывает смещение максимума в более низкие температуры. Существует некое критическое значение ширины барьера, между 1 и 2 в наших единицах, выше которого молекулярная резонансная диффузия начинает играть значительную роль. Это значение при высоте барьера 20000К равно приблизительно 0.2 Å. Аналогичные расчеты были проведены также с различной высотой барьера. Как и следовало ожидать, значение максимума также растет с ростом высоты. молекулярная резонансная диффузия в значительной мере определяется шириной барьера. Рост ширины барьеров вызывает смещение максимума в более низкие температуры. Существует некое критическое значение ширины барьера, между 1 и 2 в наших единицах, выше которого молекулярная резонансная диффузия начинает играть значительную роль. Это значение при высоте барьера 20000К равно приблизительно 0.2 Å. Аналогичные расчеты были проведены также с различной высотой барьера. Как и следовало ожидать, значение максимума также растет с ростом высоты.
На рисунке 5 представлены расчеты, демонстрирующие влияние «дна» между двумя барьерами. Выбран пример гауссового потенциала.
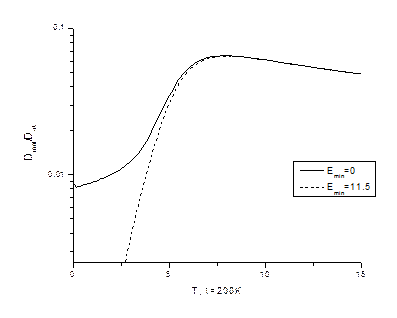
Рисунок 5 – Учет влияния минимального значения возможного резонансного прохождения. Расчеты при параметрах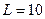 , , 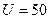 и и 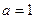
Из рисунка видно, что отсутствие низкоэнергетических резонансов не влияет существенно на общую картину – существенно меняется только начало кривой, далекое от положения максимума.
Заключение
В результате проделанных вычислений можно сделать следующие выводы о характере молекулярной резонансной диффузии в твердом теле:
– существенное значение имеет размер свободной области между двумя барьерами, а именно – линейный параметр должен быть выше некоторого значения. Для нашего случая это примерно 2 Å.
– определяющее значение имеет ширина барьеров. В районе величины 2 Å при высоте барьера в 20000 К молекулярная резонансная диффузия превышает атомарную.
– для реальных потенциалов значение минимального уровня, при котором возможно резонансное прохождение, не влияет существенно на характер молекулярной диффузии в районе максимума.
Возможно продолжение расчетов для более реальных моделей и с другими параметрами потенциалов.
Список использованных источников
1. N. Saito and Y. Kayanuma, J. Phys.: Condens. Matter 6
, 3759 (1994) .
2. F. M. Pen’kov, Phys. Rev. A 62,
044701-1,4 (2000).
3. G. L. Goodvin and M.R.A. Shegelski, Phys. Rev. A 71
,
032719-1,10 (2005).
4. E. Pijper and A. Fasolino, The Journal of Chemical Physics 126, 014708-1,10 (2007)
5. Mark R.A. Shegelski [et al] Rhys. Rew A 77, 032702-1,12 (2008).
6. П.М. Красовицкий, Ф.М. Пеньков Материалы 5-й международной конференции «Ядерная и радиационная физика», Алматы, 2006. Т. 2, с. 468
7. Я. И. Френкель, Собрание избранных трудов, т III, Издательство АН СССР, Москва-Ленинград, 1959 г.
|