С.А. Клоков, Омский государственный университет, кафедра математического анализа
1. Введение. Обозначения. Постановка задачи
Пусть 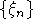 - стационарная (в узком смысле) последовательность случайных величин (с.в.), - стационарная (в узком смысле) последовательность случайных величин (с.в.), 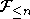 , , 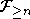 - -  -алгебры, порожденные семействами -алгебры, порожденные семействами 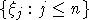 , , 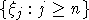 . Говорят, что . Говорят, что 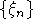 удовлетворяет условию равномерно сильного перемешивания (РСП), если коэффициент перемешивания удовлетворяет условию равномерно сильного перемешивания (РСП), если коэффициент перемешивания
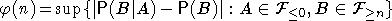
стремится к нулю при 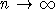 . .
Как обычно, через 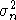 обозначим дисперсию суммы обозначим дисперсию суммы 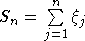 , а через , а через 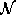 - нормальную с.в. с нулевым математическим ожиданием и единичной дисперсией. Символы - нормальную с.в. с нулевым математическим ожиданием и единичной дисперсией. Символы 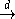 и и 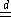 обозначают сходимость по распределению и равенство распределений с.в., · - норму в L2, 1(A) - индикатор множества A. Через обозначают сходимость по распределению и равенство распределений с.в., · - норму в L2, 1(A) - индикатор множества A. Через 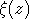 обозначим срезку обозначим срезку 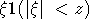 , через , через 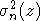 - дисперсию суммы - дисперсию суммы 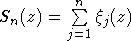 . Вместе с последовательностью . Вместе с последовательностью 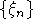 будет рассматриваться последовательность будет рассматриваться последовательность 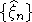 таких с.в., что таких с.в., что 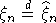 и и 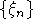 независимы. В случае, если функции f и g связаны соотношением независимы. В случае, если функции f и g связаны соотношением 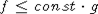 , где const - абсолютная константа, будем писать , где const - абсолютная константа, будем писать  , а если , а если  и и 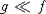 , то , то 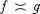 . .
Будем считать известными определения правильно меняющихся и медленно меняющихся функций (см., например, [5]).
Говорят, что последовательность с.в. 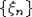 притягивается к нормальному закону, если при некотором выборе нормирующих констант An и притягивается к нормальному закону, если при некотором выборе нормирующих констант An и 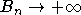 имеет место соотношение имеет место соотношение 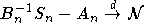 , , 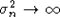 . В случае, если с.в. . В случае, если с.в. 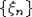 имеют конечные вторые моменты, дисперсия суммы имеют конечные вторые моменты, дисперсия суммы 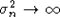 и и 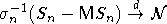 говорят, что к последовательности применима центральная предельная теорема (ЦПТ). говорят, что к последовательности применима центральная предельная теорема (ЦПТ).
Первые предельные теоремы для слабо зависимых величин были доказаны И.А. Ибрагимовым в начале 60-х годов. Условие РСП дает возможность доказывать результаты о сходимости к нормальному закону без каких-либо предположений о скорости перемешивания (стремления 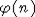 к нулю). В этом случае будем говорить, что справедливо строгое притяжение к нормальному закону. В [?] доказана к нулю). В этом случае будем говорить, что справедливо строгое притяжение к нормальному закону. В [?] доказана
Теорема 1. Пусть 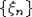 - стационарная последовательность с.в., удовлетворяющая условию РСП, - стационарная последовательность с.в., удовлетворяющая условию РСП, 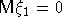 , , 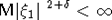 для некоторого для некоторого 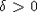 и и 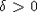 . Тогда к последовательности . Тогда к последовательности 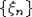 применима ЦПТ. применима ЦПТ.
Для последовательности независимых одинаково распределенных с.в. ЦПТ справедлива, если потребовать существование лишь вторых моментов. Исходя из этого, в [1] высказана
Гипотеза (Ибрагимов, 1965).
Пусть 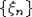 - стационарная последовательность с.в., удовлетворяющая условию РСП, - стационарная последовательность с.в., удовлетворяющая условию РСП, 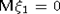 и и 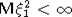 . Тогда к последовательности . Тогда к последовательности 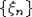 применима ЦПТ. применима ЦПТ.
Пусть 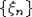 - последовательность независимых одинаково распределенных с.в., не имеющих вторых моментов. Тогда распределение - последовательность независимых одинаково распределенных с.в., не имеющих вторых моментов. Тогда распределение 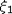 принадлежит области притяжения нормального закона тогда и только тогда, когда функция принадлежит области притяжения нормального закона тогда и только тогда, когда функция 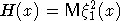 является ММФ. Иосифеску сформулировал следующее предположение. является ММФ. Иосифеску сформулировал следующее предположение.
Гипотеза (Ибрагимов-Иосифеску).
Пусть 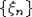 - стационарная последовательность с.в., удовлетворяющая условию РСП с - стационарная последовательность с.в., удовлетворяющая условию РСП с 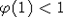 , , 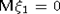 и H(x) - ММФ. Тогда и H(x) - ММФ. Тогда 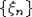 притягивается к нормальному закону. притягивается к нормальному закону.
Гипотезы Ибрагимова и Ибрагимова-Иосифеску не доказаны и не опровергнуты до сих пор.
Хорошо известны два достаточных условия для медленного изменения H(x): существование конечного второго момента (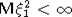 ) и правильное изменение хвоста распределения одного слагаемого ( ) и правильное изменение хвоста распределения одного слагаемого (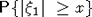 - ПМФ порядка -2). В работе [4] доказана - ПМФ порядка -2). В работе [4] доказана
Теорема 2. Пусть 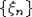 - стационарная последовательность с.в., удовлетворяющая условию РСП, причем - стационарная последовательность с.в., удовлетворяющая условию РСП, причем 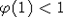 . Пусть . Пусть 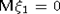 , выполнено соотношение , выполнено соотношение
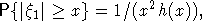 (1) (1)
где h(x) - ММФ. Тогда 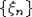 притягивается к нормальному закону. притягивается к нормальному закону.
В настоящей работе показано, что теорема 2 остается справедливой, если на функцию h(x) из (1) наложить более слабое ограничение, чем медленное изменение. В монографии Е.Сенеты предложено обобщение понятия ММФ. Функция h(x) называется SO-меняющейся [3], если существуют такие положительные постоянные C1 и C2, что для всех 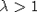 выполнено выполнено
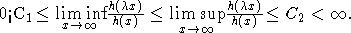 (2) (2)
Очевидно, что ММФ h(x) удовлетворяет (2), но не наоборот. Примерами SO-меняющихся функций могут служить любые функции, отделенные от нуля и от бесконечности. Таким образом, введенное расширение класса ММФ является нетривиальным.
Основным результатом работы является обобщение теоремы 2:
Теорема 3. Пусть 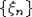 - стационарная последовательность с.в., удовлетворяющая условию РСП, - стационарная последовательность с.в., удовлетворяющая условию РСП, 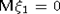 и выполнено соотношение и выполнено соотношение
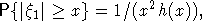 (3) (3)
где h(x) - SO-меняющаяся функция. Тогда 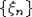 притягивается к нормальному закону. притягивается к нормальному закону.
Обобщение результата M. Пелиграда стало возможным благодаря уточнению доказательства теоремы 2, данного в работе [4].
2. Вспомогательные результаты
Из (2) очевидным образом следует
Лемма 1. Пусть h(x) - SO-меняющаяся функция. Тогда 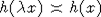 для любого фиксированного для любого фиксированного 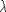 и для любой функции и для любой функции 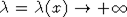 достаточно медленно. достаточно медленно.
Определим последовательность 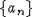 соотношением соотношением 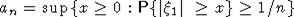 . .
Лемма 2. Пусть выполнено (3). Тогда
а) 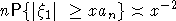 для любого x0 или для любого x0 или 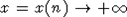 достаточно медленно; достаточно медленно;
б) если целое число k фиксировано или целочисленная последовательность 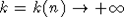 достаточно медленно, то достаточно медленно, то 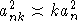 . .
Доказательство. Из определения an легко выводится, что
 (4) (4)
Из (4) и леммы 1 следует, что
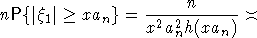
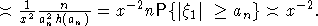 (5) (5)
Пункт а) доказан. Теперь докажем б). Пусть D0 - некоторая константа. Из (4) и леммы 1, аналогично (5), выводим для любого фиксированного k или 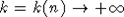 достаточно медленно, что достаточно медленно, что
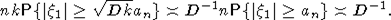 . .
Выбором достаточно большой константы 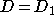 можно добиться, что можно добиться, что 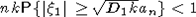 , откуда следует, что , откуда следует, что 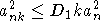 . Выбирая достаточно малую константу в = D2, получим, что . Выбирая достаточно малую константу в = D2, получим, что 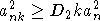 . Таким образом, . Таким образом, 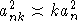 . .
Лемма 3. Пусть 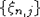 - схема серий с.в. с конечными вторыми моментами, в каждой серии с.в. - схема серий с.в. с конечными вторыми моментами, в каждой серии с.в. 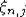 образуют стационарную последовательность, удовлетворяющую условию РСП с одним и тем же коэффициентом перемешивания образуют стационарную последовательность, удовлетворяющую условию РСП с одним и тем же коэффициентом перемешивания 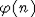 причем причем 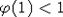 . Пусть Tn,j . Пусть Tn,j 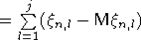 , ,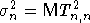 . Тогда . Тогда
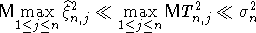 (6) (6)
Доказательство. Первое неравенство в (6) доказано в предложении 3.3 из [4], а второе выведено в [3, лемма3.3].
Лемма 4. Для любого фиксированного k или 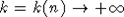 достаточно медленно выполнено соотношение достаточно медленно выполнено соотношение 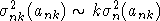 . .
Доказательство. Схема доказательства приведена в [?, теорема 18.2.3].
Лемма 5. Пусть k = k(n) - целочисленная последовательность, достаточно медленно стремящаяся к бесконечности, и имеет место (3). Тогда
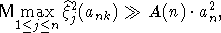 (7) (7)
где 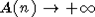 при при 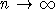 . .
Доказательство. Для проведения оценки (7) используются идеи M. Пелиграда, предложенные в [4]. В силу пункта б) леммы 2 существует такая константа C0, что 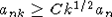 . Пусть . Пусть 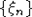 - такая числовая последовательность, что - такая числовая последовательность, что 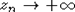 и zn = o(Ck1/2). Тогда, имея в виду пункт а) леммы 2, легко видеть, что для и zn = o(Ck1/2). Тогда, имея в виду пункт а) леммы 2, легко видеть, что для 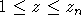
Из (8) выводим
где 0 - некоторая константа. Пользуясь пунктом а) леммы 2, нетрудно вычислить, что 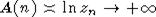 при при 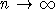 . .
3 Доказательство основного результата
В работе А.Г. Гриня [?] введено понятие универсальной нормирующей последовательности (УНП) 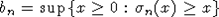 . Там же доказана . Там же доказана
4. Пусть 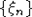 - стационарная последовательность, удовлетворяющая условию РСП. Для того чтобы - стационарная последовательность, удовлетворяющая условию РСП. Для того чтобы 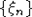 притягивалась к нормальному закону, достаточно, а если притягивалась к нормальному закону, достаточно, а если 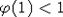 , и необходимо, чтобы при любом , и необходимо, чтобы при любом 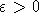 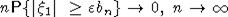 . Пусть k = k(n) - целочисленная последовательность, стремящаяся к бесконечности столь медленно, что одновременно справедливы леммы 2, 4, 5. Тогда, имея в виду еще и лемму 3, получаем . Пусть k = k(n) - целочисленная последовательность, стремящаяся к бесконечности столь медленно, что одновременно справедливы леммы 2, 4, 5. Тогда, имея в виду еще и лемму 3, получаем
Вместе с определением УНП (9) означает, что 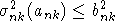 и an2 = o(bn2). Пусть последовательность q = q(n) стремится к бесконечности столь медленно, что an2 = o(q-1bn2). Пользуясь пунктом а) леммы 2, имеем для любого и an2 = o(bn2). Пусть последовательность q = q(n) стремится к бесконечности столь медленно, что an2 = o(q-1bn2). Пользуясь пунктом а) леммы 2, имеем для любого 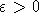
при 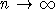 . Согласно теореме 4, последовательность . Согласно теореме 4, последовательность 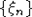 притягивается к нормальному закону. Теорема доказана. притягивается к нормальному закону. Теорема доказана.
Список литературы
Ибрагимов И.А., Линник Ю.В. Независимые и стационарно связанные величины. М.: Наука, 1965. 524 с.
Гринь А.Г. Об областях притяжения для сумм зависимых величин // Теория вероятн. и ее применен. 1990. Т. 35. N2. С. 255-270.
Peligrad M. An invariance principle for  -mixing sequences. - Ann. Probab. 1985. V. 13. N4. Р. 1304-1313. -mixing sequences. - Ann. Probab. 1985. V. 13. N4. Р. 1304-1313.
Peligrad M. On Ibragimov-Iosifescu conjecture for  -mixing sequences // Stochastic Processes and their Applications. 1990. V. 35. P. 293-308. -mixing sequences // Stochastic Processes and their Applications. 1990. V. 35. P. 293-308.
Сенета Е. Правильно меняющиеся функции. М.: Наука, 1985. 142 с.
|