Вычисление определителя методом Гаусса с выбором главного элемента
ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЯ МЕТОДОМ ГАУССА С ВЫБОРОМ ГЛАВНОГО ЭЛЕМЕНТА.
Одновременно с решением системы линейных алгебраических уравнений
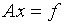
можно вычислить определитель матрицы А.
Пусть в процессе исключения найдено распожение
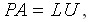
т.е. построены матрицы L и U . Тогда
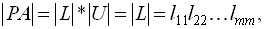
и, таким образом, произведение диагональных елементов матрицы L (ведущих, главных елементов метода исключения) равно определителю матрицы РА. Поскольку матрицы РА и А отличаются только перестановкой строк, определитель матрицы РА может отличаться от определителей матрицы А только знаком.
А именно, 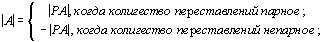
Таким образом, для вычисления определителя необходимо знать, сколько перестановок было осуществлено в процессе сключения.
Если матрица А выроджена, то при использовании метод Гаусса с выбором главного элемента по столбцу на некотором шаге исключения К все элементы которого столбца, находящиеся ниже главной диагонали и на ней, окажутся равными нулю.При этом дальнейшее исключение становится невозможным и программа должна выдать информацию о том, что определитель матрицы равен нулю.
ОБРАЩЕНИЕ МАТРИЦ.
Нахождение матрицы, обратной матрице А , еквивалентно решению матричного уравнения
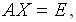 (1)
(1)
где Е - единичная матрица, X - искомая квадратная матрица.
Уравнение (1) можно записать в виде системы 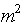 уравнений
уравнений
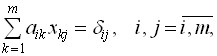 (2)
(2)
где 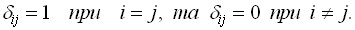
Можно заметить, что система (2) распадается на m независимых систем уравнений с одной и той же матрицей А , но с различными правыми частями. Эти системы имеют
вид ( фиксируем j ) :
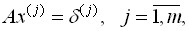 (3)
(3)
где 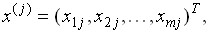 у вектора - столбца
у вектора - столбца 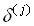 равна единице j-та компонента и равны нулю остальные компоненты.
равна единице j-та компонента и равны нулю остальные компоненты.
Например, для матрицы второго порядка система (2) распадается на две независимые системы:

Для решения систем (3) используется метод Гаусса ( обычный или с выбором главного элемента).
Рассмотрим применение метода Гаусса без выбора главного элемента. Поскольку все системы (3) имеют одну и ту же матрицу А , достаточно один раз совершить прямой ход метода Гаусса, т.е. получить разложение A=LU и запомнить матрицы L i U .
Обратный ход осуществляется путем решения систем уравнений 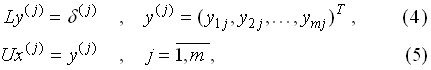
с треугольными матрицами L и U.
При осуществлении обратного хода можно сократить число действий, принимая во внимание специальный вид правых частей системы (4).
Запишем подробнее первые j-1 уравнений системы (4):
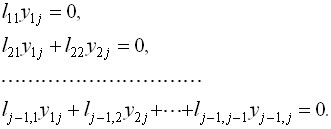
Учитывая невырожденность матрицы L ( т.е. 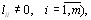
отсюда получаем
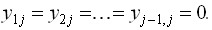
При этом оставшиеся уравнения системы (4) имеют вид 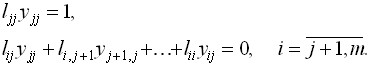
Отсюда последовательно находятся неизвестные 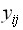 по формулам:
по формулам: 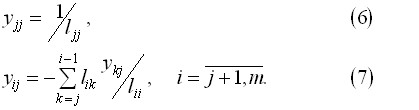
Можно показать, что общее число действий умножения и деления, необходимое для обращения матрицы указанным способом, порядка 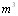 . Тем самым обращение матрицы требует не намного больше времени, чем решение системы уравнений.
. Тем самым обращение матрицы требует не намного больше времени, чем решение системы уравнений.
Вместе с этим смотрят:
Вычисление элементарных функцийГамма функцииГеометрическая прогрессияГеометрия Лобачевского